 本章介绍了机器学习中一些“上帝视角”,包括对目标函数的理解、统一的神经网络框架等。
本章介绍了机器学习中一些“上帝视角”,包括对目标函数的理解、统一的神经网络框架等。
3. 机器学习中的统一框架
很多机器学习问题都可以放在一个统一框架下讨论,这样大家在理解各种模型时就是相互联系的。
3.1 目标函数
回忆一下目标函数的定义:
\[w^*=\operatorname*{argmin}\limits_{w} \sum_{i=1}^N\underbrace{L(m_i(w))}_{Bias}+\underbrace{\lambda Reg(w)}_{Variance}\]
很多模型可以用这种形式框起来,比如linear regression、logistic regression、SVM、additive models、k-means,neural networks 等等。其中损失函数部分用来控制模型的拟合能力,期望降低偏差,正则项部分用来提升模型泛化能力,期望降低方差,最优模型是对偏差和方差的最优折中。
3.1.1 损失函数
损失函数反应了模型对历史数据的学习程度,我们期望模型能尽可能学到历史经验,得到一个低偏差模型。
Q:大家想想横坐标是什么?
\[ \begin{array}{l} \text{0-1 loss: }&L_{01}(m_i(w))=\amalg(m_{i}(w) \le 0)\\ \text{squared loss: }&L_{2}(m_i(w))=\frac{1}{2}(m_{i}(w) -1)^2\\ \text{hinge loss: }&L_{hinge}(m_i(w))=max(0,1-m_{i}(w))\\ \text{log loss: }&L_{log}(m_i(w))=log(1+e^{-m_{i}(w)})\\ &\text{where $m$ is called 'margin'.} \end{array} \]
实践当中很少直接使用0-1损失做优化(当然也有这么用的如:Direct 0-1 Loss Minimization and Margin Maximization with Boosting 和 Algorithms for Direct 0–1 Loss Optimization in Binary Classification,但总的来说应用有限),原因如下:
- 0-1损失的优化是组合优化问题且为NP-hard,无法在多项式时间内求得;
- 损失函数非凸非光滑,很多优化方法无法使用;
- 对权重的更新可能会导致损失函数大的变化,即变化不光滑;
- 只能使用\(L_0\)正则,其他正则形式都不起作用;
- 即使使用\(L_0\)正则,依然是非凸非光滑,优化求解困难。
由于0-1损失的问题,所以以上损失函数都是对它的近似。原理细节可以参考:Understanding Machine Learning: From Theory to Algorithms
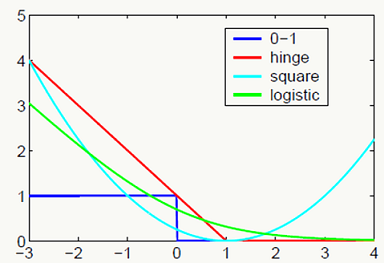
不同损失函数在相同数据集下的直观表现如下: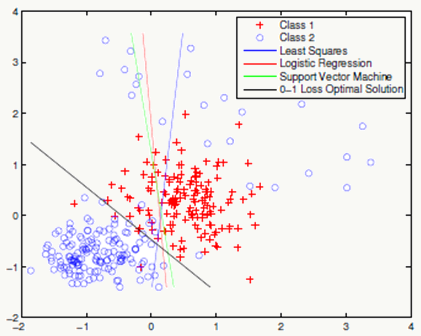
3.1.2 正则化项
正则化项影响的是模型在未知样本上的表现,我们希望通过它能降低模型方差提高泛化性。
如果有数据集:
\[D=\{(x_i,y_i)|i=1,2,3,...N\}\] 在给定假设下,通常采用极大似然估计(MLE)求解参数:
\[w^*=\operatorname*{argmin}\limits_{w} \prod_{i=1}^N{-p(y_i|x_i;w)}=\operatorname*{argmin}\limits_{w} \sum_{i=1}^N{-log~p(y_i|x_i;w)}\]
假设模型参数也服从某种概率分布: \(w \sim p(w)\), 可以采用极大后验概率估计(MAP)求解参数。 \[ \begin{array}{l} w^*=\operatorname*{argmin}\limits_{w} \prod_{i=1}^N{-p(w|x_i,y_i)}\\ ~~~~=\operatorname*{argmin}\limits_{w}\sum_{i=1}^N{-log~p(w|x_i,y_i)}\\ ~~~~=\operatorname*{argmin}\limits_{w}\sum_{i=1}^N{-log~p(x_i,y_i|w)p(w)}\\ ~~~~=\operatorname*{argmin}\limits_{w}\sum_{i=1}^N{-log~p(x_i,y_i|w)-log~p(w)}\\ ~~~~= \left\{ \begin{array}{1} \text{generative model} & \operatorname*{argmin}\limits_{w}\sum_{i=1}^N[{\underbrace{-log~p(x_i,y_i|w)}_{Bias}-\underbrace{log~p(w)}_{Variance}}] \\ \text{discriminative model} & \operatorname*{argmin}\limits_{w}\sum_{i=1}^N[{\underbrace{-log~p(y_i|x_i;w)}_{Bias}-\underbrace{log~p(w)}_{Variance}}] \end{array} \right. \end{array} \]
3.1.3 L2 正则
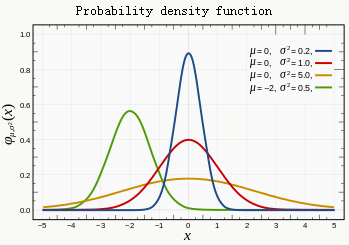
假设 \(w_j \sim N(0,\delta_j^2)\) \[ \begin{array}{l} \because p(w_j)=\frac{1}{\sqrt{2\pi}\delta}e^{-\frac{w^2}{2\delta^2}}\\ \therefore Reg(w)=\sum_{i=1}^mw_i^2,\text{ m is the number of weights.} \end{array} \]
3.1.4 L1 正则
假设 \(w_j \sim Laplace(0,b_j)\)
\[ \begin{array}{l} \because p(w_j)=\frac{1}{2b}e^{-\frac{|w_j|}{b}}\\ \therefore Reg(w)=\sum_{i=1}^m|w_i|,\text{ m is the number of weights.} \end{array} \]
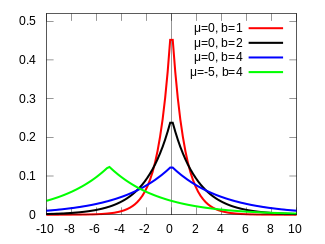
3.1.5 正则化的几何解释
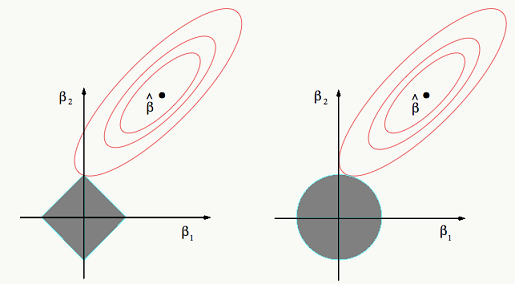
给定向量\(w = (w_1,..., w_n)\), 定义 \(L_q\)正则,其中 \(n > 0\):
\[ \begin{array}{l} \parallel w \parallel_q=\sqrt[q]{\sum_{i=1}^n|w_i|^q}\\ \text{when $q=0$ we define $l_0$-norm to be the number of non-zero elements of the vector:}\\ \parallel w \parallel_0=\#~(i|x_i \ne 0)\\ \end{array} \]
不同q的取值下正则项的几何表现如下: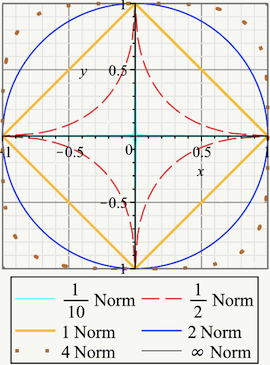
3.1.6 Dropout正则化与数据扩充
这两类方法在神经网络中比较常用,后面会专门介绍。
3.2 神经网络框架
很多模型可以看做是神经网络,例如:感知机、线性回归、支持向量机、逻辑回归等
3.2.1 Linear Regression
线性回归可以看做是激活函数为\(f(x)=x\)的单层神经网络: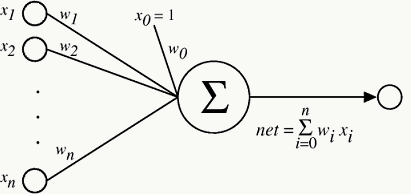
3.2.2 Logistic Regression
逻辑回归可以看做是激活函数为\(f(x)=\frac{1}{1+e^{-x}}\)的单层神经网络: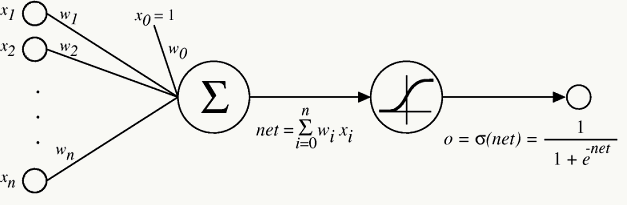
3.2.3 Support Vector Machine
采用核方法后的支持向量机可以看做是含有一个隐层的3层神经网络: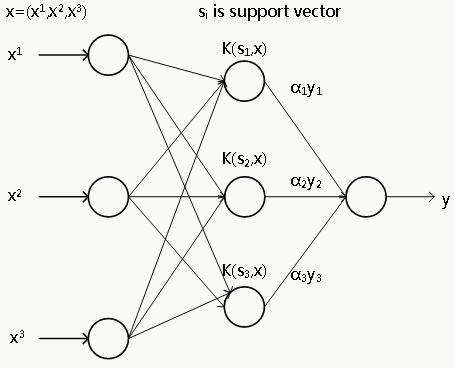
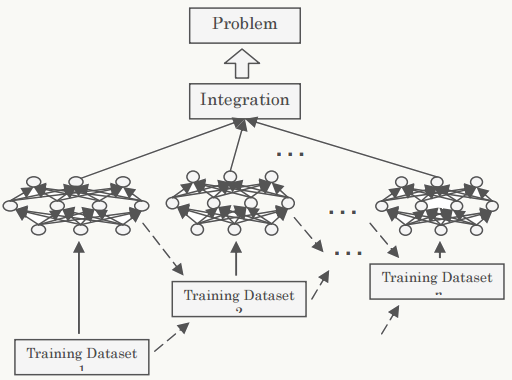
3.2.4 Bootstrap Neural Networks
采用bagging方式的组合神经网络: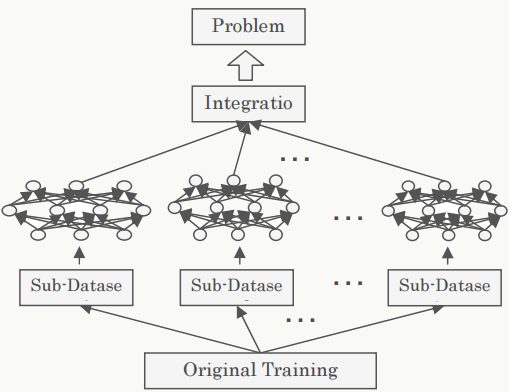
3.2.5 Boosting Neural Network
采用boosting方式的组合神经网络: