 本文对0-1规划及其实际应用做了简单介绍。
本文对0-1规划及其实际应用做了简单介绍。
0-1规划及其实际应用
什么是最优化问题
最优化问题历史
以下发展史部分主要参考《History of Optimization》一文。
1、古代
公元前3000年左右,古埃及、古印度、古巴比伦就出现了最早的、文字记录的关于几何(如,长度、角度等)的经验性总结。 而最早的优化问题在古希腊数学家研究几何相关问题时出现,尤其是到了 公元前300年,欧几里得(Euclid) 完成了著名的数学巨著《几何原本》,他在研究关于点与线之间最小距离的问题时,证明了在给定总边长的矩形中,正方形的面积最大,而其本质就是个最优化问题求解。
公元前200年,Zenodorus 在研究Dido问题(即等周问题:在平面上,所有给定周长的闭合曲线中,是否有具有最大面积的曲线?【圆】)时,同样是在研究一个最优化问题。
公元前100年,Heron 在研究光在镜面的反射问题时,证明光在两点之间通过最短长度的路径传播,这个问题也是个最优化问题。
2、在变分法(微积分的一种推广) 被发明之前,数学家们仅是在非系统性的研究一些优化问题的个例。
1615年,开普勒(J.Kepler) 提出了求解酒桶最佳尺寸的方法,以及求解秘书问题(要聘请一名秘书,有\(n\)个应聘者,每次只能面试1人且结束后要立刻决定是否通过,如果当时拒绝则候选人不会再回来。假设,面试过程能完全了解候选人的能力,且能与之前所有面试了的候选人做比较。那么采取什么策略,可以使最优候选人被留下的概率最大?【\(\frac{1}{e}\)】)的方法。
1638年,伽利略(G.Galilei ) 研究但失败的吊链形状问题,最终由莱布尼茨(Leibniz)和雅各布·伯努利(Johann Bernoullii)分别独立解决。
1636年,费马(P.de Fermat ) 证明了对于连续可微函数在极值点处的导数为0,以及光会沿着两点之间最短距离传播,此时传播的时间最短。
3、牛顿(I.Newton)和莱布尼茨(G.W. von Leibniz) 分别发明微积分后,为变分法的出现提供了基础理论。
1687年,牛顿 研究了最小阻力体问题,它是历史上第一个变分法问题。
1696年,伯努利兄弟(Johann and Jacob Bernoulli) 研究 Brachistochrone问题时诞生了变分法。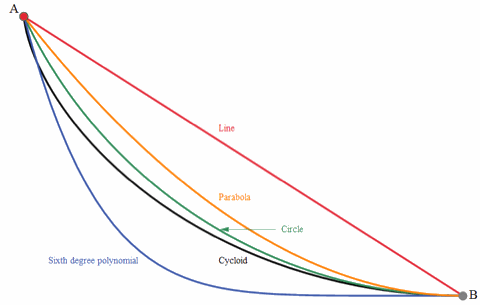
1740年,欧拉(L.Euler) 出版了关于变分法一般理论的研究。
1746年,皮埃尔·路易·莫佩尔蒂(P.L.M. de Maupertuis) 使用最小作用量原理(或叫平稳作用量原理)来解释物理现象,它是一种变分原理,为后续分析力学(高度数学表达的经典力学)奠定了核心基础。
1754年,拉格朗日(J.-L. Lagrange) 在其19岁时首次做出他在变分法研究上的发现,并在1760年提出关于极小曲面的问题(Plateau's problem,研究当边界固定时极小表面的存在性问题)。该问题在1936年才被道格拉斯(J. Douglas)解决并因此获得了数学界的诺贝尔奖——菲尔兹奖(Fields Medal),1974年邦别里(E.Bombieri)也因为对这个问题的研究获得了菲尔兹奖。
1784年,加斯帕尔·蒙日(G.Monge) 提出了关于组合优化的问题,被称作最优运输问题(optimal transport),简单描述是,假设有已知位置的\(N\)个仓库,每个仓库有\(G\)个物资,需要将这些物资分发到已知位置和需求量的\(M\)个不同的地方,怎么运输才能使总的运输效率最高?这个问题非常经典,二战后苏联的列昂尼德·坎托罗维奇在该领域取得了重大进展,对原始问题做了松弛处理,使得该问题在实际应用中发扬光大,一般也叫做Monge-Kantorovich问题,围绕着这个问题也使多人获得菲尔兹奖,这个问题也为后续线性规划的发展奠定了基础, 同时在机器学习领域,该问题也是近几年的热点,大家熟知的对抗生成神经网络Wasserstein GAN背后就有其理论的支撑。
4、19世纪,数学家们提出了第一个优化算法,并在后续对变分法的逐步完善中走向实际应用,在经济活动研究中扮演了重要角色,比较有代表性的成果有:
1860年,勒让德(Legendre)和高斯(Gauss) 分别提出了最小二乘法(least square method),之前章节也聊过,最小二乘法另一个视角是假设数据的概率分布服从\(Gaussian(0,\sigma ^2)\),做极大似然估计后的结果。
1826年,傅立叶(J.B.J. Fourier ) 提出线性规划(LP)以解决力学和概率论中出现的问题。
1847年,柯西(A.L. Cauchy) 提出了梯度法。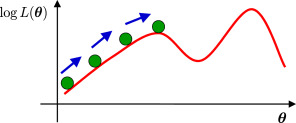
5、20世纪,变分法 得到了更进一步的发展。
1902年,法卡斯(J. Farkas) 提出了其著名引理,并被后人用于证明Karush-Kuhn-Tucker定理,KKT条件是非线性最优化问题能有最优解的必要条件。
1905年,詹森(JJ.L.W.V. Jensen) 提出了凸概念并引入凸函数,这一思想最早在哈达玛(J.S. Hadamard,1883年),霍尔德(O.L. Hölder,1889年)和奥斯托尔(O. Stolz,1893年)等人的研究中出现。
1911年,明可夫斯基(H. Minkowski) 做出了他关于凸集的第一个研究成果。
1917年,汉考克(H. Hancock) 出版了第一本关于最优化的书:《极小值和极大值理论(Theory of Minima and Maxima)》。
1917年,生物数学家汤普森(D.W. Thompson) 在《成长与形式(On Growth and Form)》一书中运用最优化算法分析生物体的形式。
1928年,弗兰克拉姆齐(F.P. Ramsey) 在他关于最优经济增长的研究中应用了变分法,他的研究与实践在最优增长理论发展中起到了重要作用,后者占据了现代资本理论和规划、宏观经济学、可耗尽资源、自然资源、发展经济学、金融和动态博弈的动态模型的核心部分。
1931年,维纳(J. Viner) 提出了广义包络理论(Viner-Wong envelope theorem)。
1932年,门格尔(K. Menger) 提出了旅行推销员问题的一般表述(即著名的TSP问题,给定一系列城市和每对城市之间的距离,求解访只访问每座城市一次且可以回到起始城市的最短路径),它是组合优化中的一个NP-Hard问题。
1939年,坎托罗维奇(L.V. Kantorovich) 提出了线性规划模型及其求解算法。1975年,他与T.C. Koopmans因对线性规划问题的贡献而获得了诺贝尔经济学奖。
二战后最优化与运筹学同步发展,冯·诺伊曼又是运筹学发展背后的重要人物,伴随着电子计算的发展,优化算法领域的研究不断深化和扩大。
1944年,冯·诺伊曼(J. Von Neumann)和莫根斯坦 (Morgenstern) 通过使用动态规划的思想解决了顺序决策问题。
1947年,在美国空军工作的 丹齐格(G. Dantzig) 提出了用于解决线性规划问题的单纯形法(Simplex method),同时冯·诺依曼也建立了线性规划问题的对偶理论。 1949年,第一届关于优化的“国际数学规划研讨会”在芝加哥举行,大会上一共收录了34篇论文。
1951年,库恩(H.W. Kuhn)和塔克(A.W.Tucker) 提出了非线性问题最优解的必要条件——KKT条件。ps:F.John(1948年)和W.Karush(1939年)提出过类似条件。
1951年,马科维茨(H. Markowitz) 提出了基于二次优化的投资组合理论,并在1990年获得诺贝尔经济学奖。
1954年,福特(L.R. Ford)和富尔克森(D.R. Fulkerson) 对网络问题的研究是组合优化研究的起点。 另外像拟牛顿法和共轭梯度法这类优秀的最优化算法也是在这个时期被提出。
1954年,IEEE(Institute of Electrical and Electronics Engineers) 控制系统协会成立。
1956年,苏联数学家庞特里亚金(L.S. Pontryagin) 的研究小组提出了最大值原理(Pontryagin's maximum principle)。
1957年,理查德·贝尔曼(R.Bellman) 提出了最优性原理,它是求解动态规划的基本原则之一。
1960年,约坦狄克(Zoutendijk) 提出了可行方向法来推广非线性规划的单纯形法。罗森(Rosen)、沃尔夫(Wolfe,著名的wolfe condition)和鲍威尔(Powell)也提出了类似算法。
1963年,威尔逊(Wilson) 首次提出序列二次规划。Han在1975年以及Powell在1977年重新提出了该方法。
1973年,Mathematical Optimization Society(MOS) 成立,是一个致力于促进和维护数学优化主题的高专业标准的国际组织。2010年前,它的名称是“Mathematical Programming Society”。
1984年,卡马尔卡(N. Karmarkar) 利用内点法在多项式时间内求解线性规划问题带来了内点法的繁荣发展。ps:1979年Khachiyan已经提出了第一个多项式时间算法——椭球法。
60年代和70年代发展起来的复杂性分析开始对优化理论产生影响,80年代随着计算机变得更加强大和高效,使得全局优化和大规模问题的启发式算法开始流行,90年代内点法的使用扩展到半定优化。
关于最优化原理有一本很经典的书:《Numerical Optimization》Second Edition(ps:相比国外,国内这方面书的质量就很差点意思了)。
最优化问题分类及解法
最优化问题的分类方法有很多种,比如可以这么分: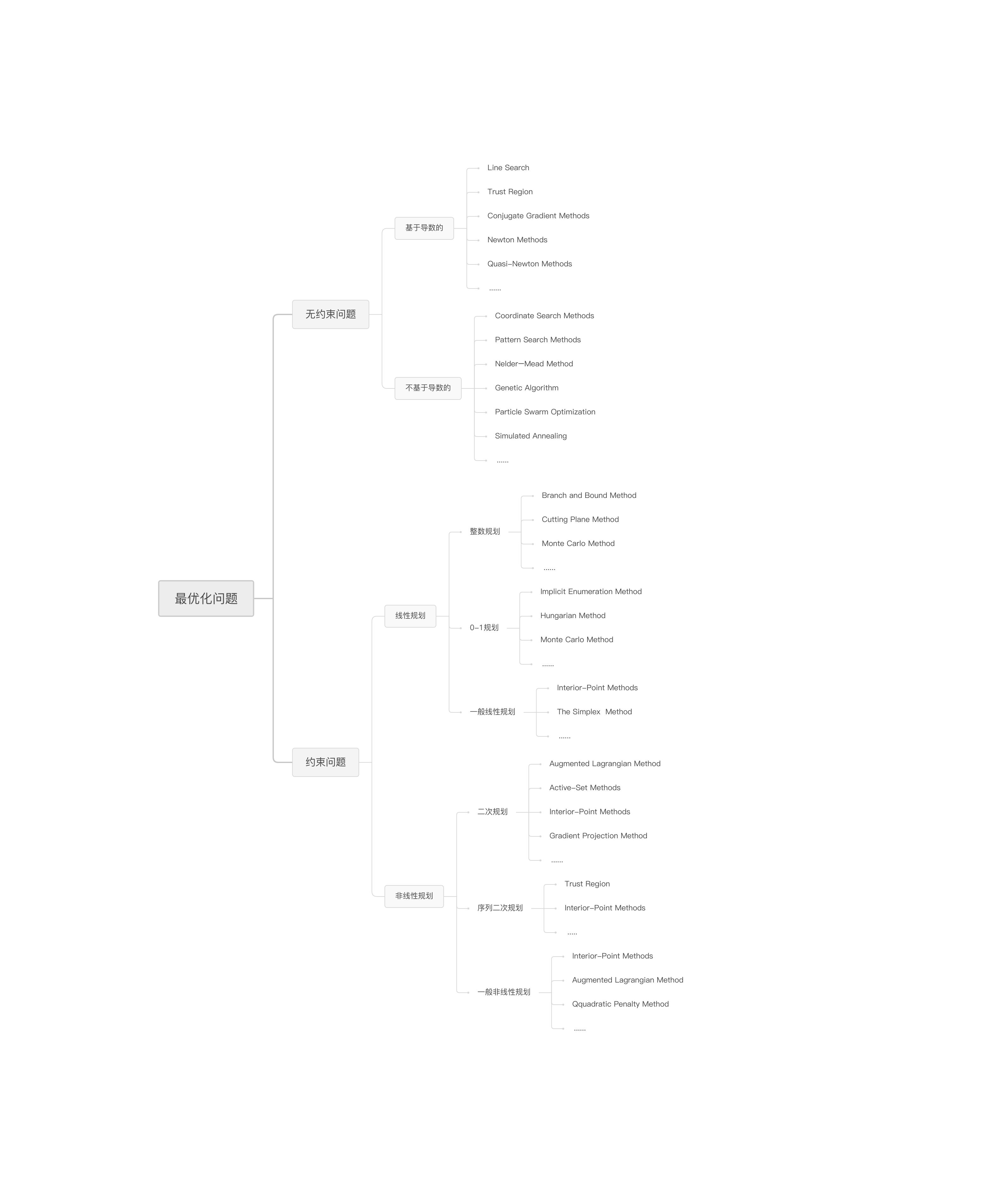
最优化问题顾名思义就是针对某个问题找到解决它的最佳方案的方法,大体上分为无约束最优化问题和约束最优化问题,对优化问题的求解,泰勒展开式是一个非常核心的基础,很多优化算法都是基于它推导出来的,这一类算法都是基于导数的,我也在《机器学习与人工智能技术分享-第四章 最优化原理》中有粗浅介绍, 基于导数的算法里又根据泰勒展开式展开到了第几项分为一阶算法和二阶算法。
最优化求解形象化来看就是:当我在沙漠中行走,希望以最快速度找到沙漠里的水源地,主要围绕着两个动作做策略,且这两个动作是连续迭代发生的:
1、往哪个方向行走;
2、行走步长如何。
最优化问题的形式化表示如下(以最小化问题为例): \[ \begin{align*} \min \text{ } & f(x)\\ \text{s.t. } & x \in X \end{align*} \] 其中\(x\)为一系列自变量,\(X\)为关于\(x\)的约束集合(就是对\(x\)的取值有什么限制),\(s.t.\)是"\(\text{subject to}\)"的缩写。上面描述的最优化求解过程就变成这样: \[ x_{t+1}=x_t-\alpha_t p_t \] 其中\(\alpha_t\)为当前阶段的步长,\(p_t\)为当前阶段的前进方向。不同的对步长的选择和方向的选择的策略会产生不同的算法,例如,当方向选择梯度方向,那么算法就变成了梯度下降算法,采用不同步长策略又会产生类似Momentum梯度下降算法、Adam、RMSprop等一阶算法,当方向选择用hessian矩阵生成时,不同估计方法又会产生牛顿法、BFGS等算法。
如果函数不可微,或者规模巨大,或者其他原因导致无法用基于导数的方法做优化,还可以选择坐标下降、遗传算法、模拟退火、粒子群这类优化算法,这里就不展开讨论了。
0-1规划问题概述
0-1规划问题定义
0-1规划属于线性规划中的整数规划中的一类特殊问题,通常用来执行“指派”任务。它的特点是:所有函数都是线性的且所有变量取值都只能是0或者1,一般形式如下: \[ \begin{align*} \min \text{ } & c^Tx\\ \text{s.t. } & Ax \leq b\\ \text{ } & x\in \{0,1\} \end{align*} \] 其中\(x\)是一系列决策变量且只能取值0或1。
看一个非常简单的例子,假设有以下坐席数据:
| 坐席 | 解决时间 |
|---|---|
| 1 | 3min/通 |
| 2 | 5min/通 |
当线上同时来了3个用户时,怎么分配坐席能让总的解决时间最短?
这是典型的任务分配问题,先做变量定义:
假设\(i\in\{1,2\}\)为某个坐席,\(j\in \{1,2,3\}\)为某个用户,\(x_{ij}\in\{0,1\}\)为第\(j\)个用户被非配给了第\(i\)个坐席变量,且该坐席解决问题时间为\(t_i\); 每个坐席一天最多处理2个用户且每个用户必须被接待。
那么上述问题就变成了以下最优化问题: \[ \begin{align*} \min \text{ } & \sum_{i=1}^2\sum_{j=1}^3 x_{ij}t_i\\ \text{s.t. } & \sum_{i=1}^2x_{ij}=1;j=1,2,3\\ \text{ } & \sum_{j=1}^3x_{ij}\leq 2;i=1,2\\ \text{ } & x_{ij}\in \{0,1\} \end{align*} \]
显然这个问题的其中一个最优解是:坐席1接待用户2和3,坐席2接待用户1,总的处理时效为:11min。
0-1规划问题解法
把上面那个问题展开: \[ \begin{align*} \min \text{ } & 3x_{11} + 3x_{12} + 3x_{13} + 5x_{21} + 5x_{22} + 5x_{23}\\ \text{s.t. } & x_{11} + x_{21}=1\tag{a}\\ \text{ } & x_{12} + x_{22}=1\tag{b}\\ \text{ } & x_{13} + x_{23}=1\tag{c}\\ \text{ } & x_{11} + x_{12} + x_{13}\leq 2\tag{d}\\ \text{ } & x_{21} + x_{22} + x_{23}\leq 2\tag{e}\\ \text{ } & x_{ij}\in \{0,1\} \end{align*} \]
解决0-1规划常用方法之一是:隐枚举法,思路如下:
1、枚举所有变量组合,如果有\(n\)个变量,则有\(2^n\)种组合,本例\(n=6\),则有64种组合方案;
2、扫描每个方案并计算目标函数值,同时按序扫描约束条件,只要有一个不满足即放弃该组合;
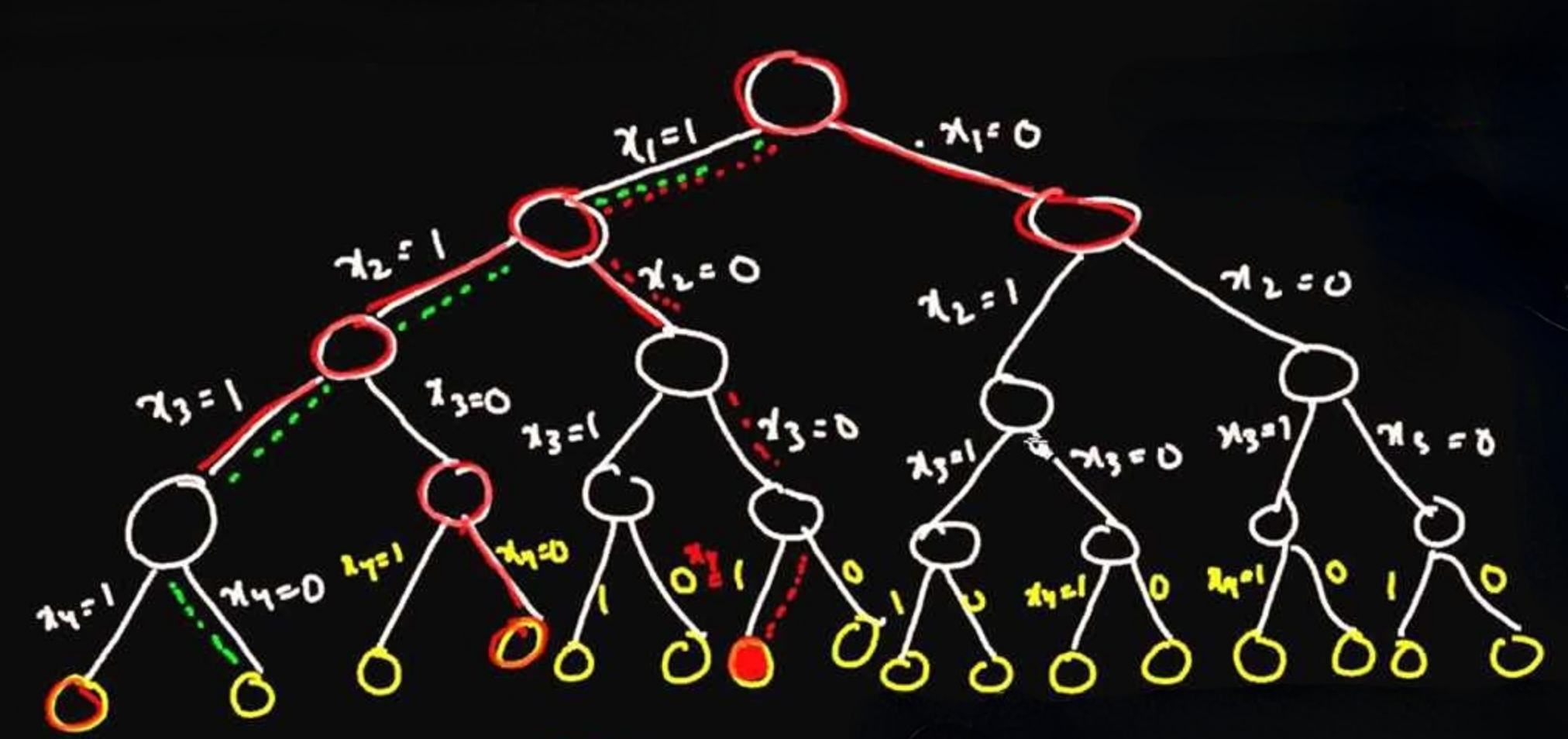
3、如果所有方案扫完都没有找到解则输出:无解,否则只要找到一个符合所有约束的解,因为这是个求最小值问题,所以可以增加一个隐条件:目标值必须小于(或者小于等于)这个解,例如: 上面那个例子在第15次搜索时找到一个解,则增加一个隐过滤条件:\(3x_{11}+3x_{12}+3x_{13}+5x_{21}+5x_{22}+5x_{23}≤13\),后续扫描只要不满足的方案直接过滤,无需扫描约束条件。
完整过程如下图:
还有其他解法,如分枝界定法、匈牙利法等,这里就不一一讨论了。
实际问题应用
问题描述
平台为用户推荐最适合的资源,在满足双方诉求的前提下最大化平台利益是一种常见场景。平台的左边是渠道用户方,右边是资源方(资源可以是资金、产品、服务等),平台居中做撮合, 随着多元化资源端入驻的越来越多,必然出现越来越复杂的多维度匹配需求,而传统的人工配置规则方式很难满足平台运营需求,所以需要有一种智能的资源与用户匹配算法。
整个资源分配的过程可以看做两个阶段:
1、定向阶段
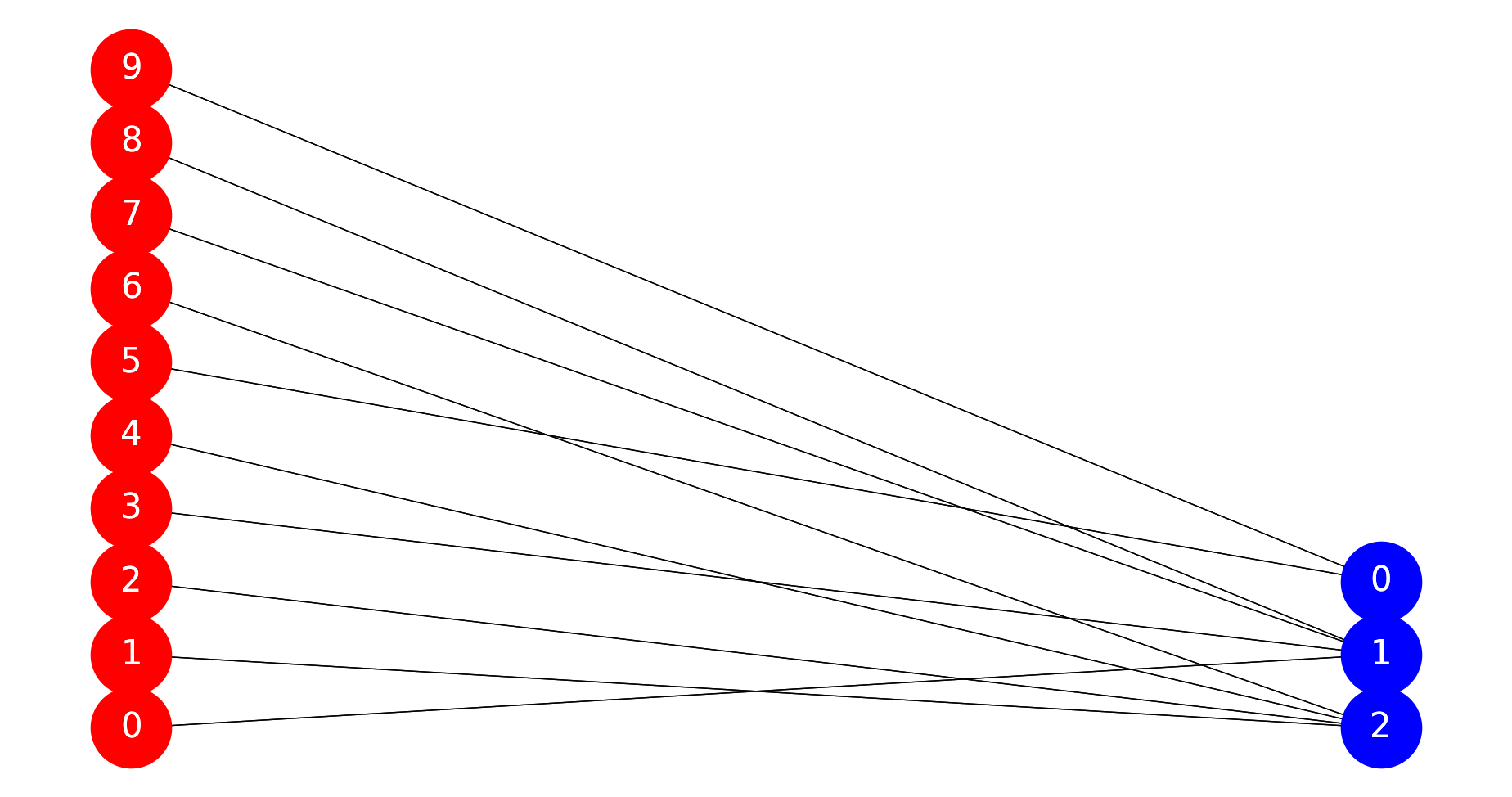
抽象出用户方和资源方的所有标签,通过标签做人群定向,初步得到用户与资源的多对多关系,包括有特殊需求的(如定向准入某个资源方)情况,进而得到当前时点的所有用户和所有资源方的二部图关系;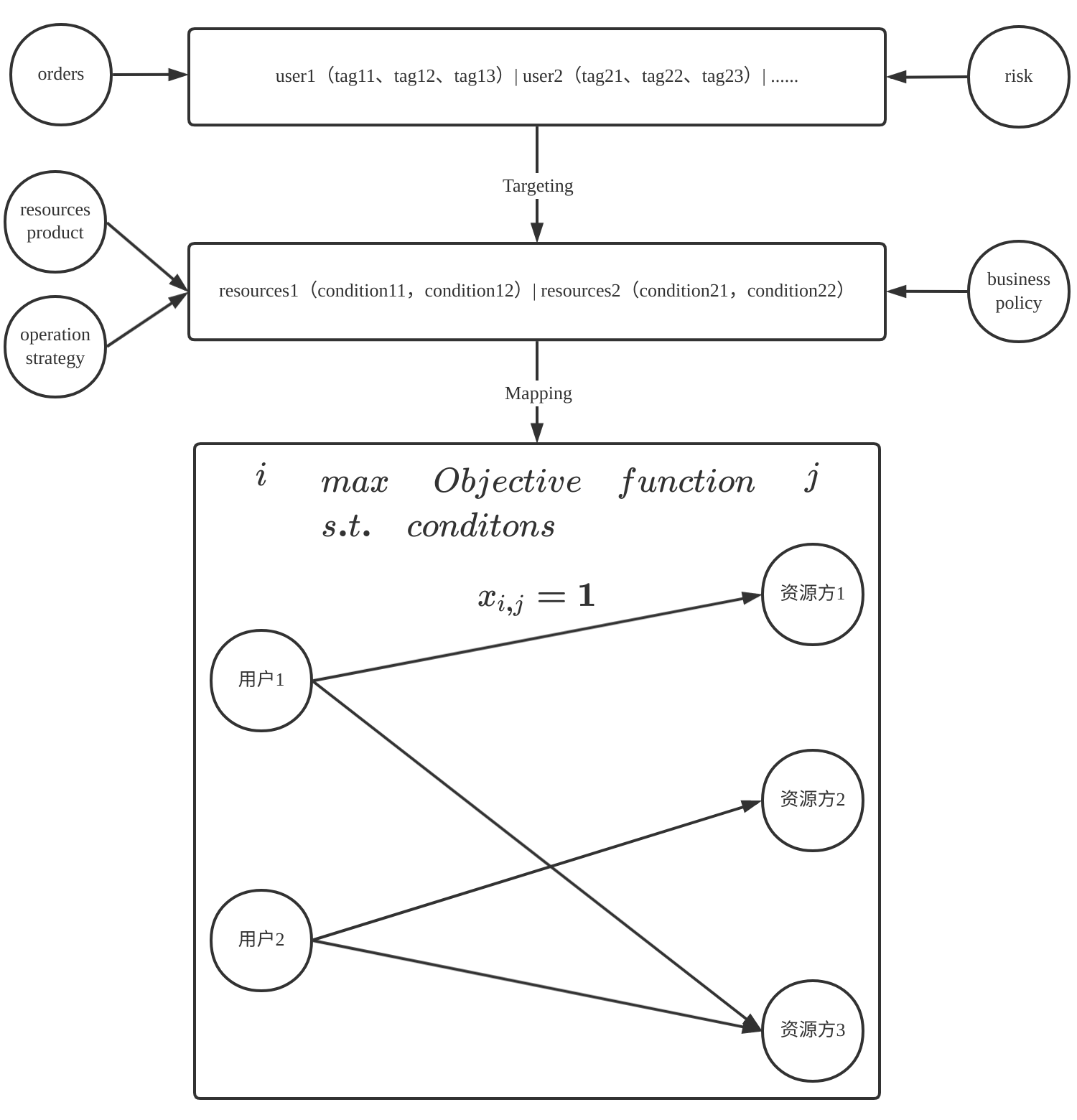
用户方 围绕着用户订单产生多种用户tag,用于后续定向,包括用户的demographic(性别、年龄等)、geographic(地域、城市、位置等)、金融需求(融资额、融资期限等)、车辆需求(品牌、车型等)、违约概率等。
资源方 围绕资源方的准入需求及资源方属性产生多种tag,例如:金融领域的授信额度、授信有效期、定向需求、逾期率要求、资金成本、展业业务范围等或者广告领域的流量需求、点击率要求、定向需求等。 用户方与资源方之间是多对多的关系,以金融领域为例,每个风控通过的用户逻辑上都要有拖底资源方承接,即用户与资源方间至少有一条边相连; 另外出于用户体验的考虑,某些情况下还会要求重新定向时匹配指定的资源方。 这一阶段的匹配,全量用户和资源方的tag都是离线生成的,当前时点新增用户的tag是在线生成的,当前时点新增资源方不予考虑(因为频率极低且会在头一天上线,离线处理即可),离线二部图的用户、资源方属性及关系会在每日做全量更新。
2、最优化求解阶段
基于平衡风险控制(或用户体验或其他要求)及订单收入的EVA最大化为优化目标,附带围绕用户与资源方关系及资源方要求为约束条件,构建0-1规划问题,当每个订单到来后,实时求解该问题的最优解,得到用户和资源方的分配方案并执行。
数学建模
以金融领域资金撮合为例,一种算法框架如下: \[ \begin{align*} &\max\quad \sum\limits_{i=1,j=1}^{n,m} x_{i,j}\cdot m_i \cdot (e(i)-pd_i\cdot lgd_i-c_j) \\ & \begin{array}{l@{\quad}r@{}l@{\quad}l} s.t. &\sum\limits_{i=1}^{n}x_{ij}\cdot m_i&\leq (1-e^{\frac{\sum\limits_{k\in \Gamma({t\leq v_j})}^{}x_{kj}\cdot m_k}{s_j}-1})\cdot s_j, &j=1,2,\ldots,m &\text{(a.) 资方$j$准入的所有用户的融资总额不能超过其授信额,且基于授信有效期,每日做额度的平滑消耗,注意对于循环额度,取消或完成订单会释放额度} \\ &\frac{\sum\limits_{i=1}^{n}x_{ij}}{\sum\limits_{i=1,j=1}^{n,m}x_{ij}}&\leq \frac{d_j\cdot(\frac{p_j}{\sum\limits_{k=1}^{m}p_k})}{\sum\limits_{j=1}^{m}d_j\cdot(\frac{p_j}{\sum\limits_{k=1}^{m}p_k})}, &j=1,2,\ldots,m &\text{(b.) 资方$j$承接订单的占比不能超过设定值,若其值为1则表示不受限,若通过率高则优先分配订单}\\ &\frac{\sum\limits_{i=1}^{n}x_{ij}\cdot m_i\cdot b(i)}{\sum\limits_{i=1,j=1}^{n,m}x_{ij}\cdot m_i}&\leq td_k, &i=1,2,\ldots,n;j=1,2,\ldots,m;k=1,2,\ldots,q &\text{(c.) $k$类型的业务放款额占比不能超过设定值,若其值为1则表示不受限}\\ &b(i)&=\left\{ \begin{array}{rcl} 1 & & {t(i)=k}\\ 0 & & {otherwise} \end{array} \right. ,&i=1,2,\ldots,n;k=1,2,\ldots,q&\text{用户$i$所属业务类型是$k$时指示函数取值为1,其他为0}\\ &\frac{\sum\limits_{i=1}^{n}x_{ij}\cdot pscore_i}{n}&\leq dscore_j, &i=1,2,\ldots,n;j=1,2,\ldots,m &\text{(d.) 资方$j$承接订单的平均逾期率不能超过设定值}\\ &pscore_i,dscore_j&\geq 0&i=1,2,\ldots,n;j=1,2,\ldots,m &\text{用户信用评分及资方接受的信用评分}\\ &\frac{\sum\limits_{i=1}^{n}x_{ij}\cdot pd_i}{n}\cdot\lambda&+\frac{\alpha}{\alpha+\beta}\cdot (1-\lambda) \leq dr_j, &i=1,2,\ldots,n;j=1,2,\ldots,m &\text{(e.) 资方$j$承接订单的平均逾期率(基于Beta-Binomial)不能超过设定值}\\ &\lambda&=\frac{\sum\limits_{i=1}^{n}x_{ij}}{\sum\limits_{i=1}^{n}x_{ij}+\alpha+\beta}&i=1,2,\ldots,n;j=1,2,\ldots,m&\text{平滑资方$j$承接订单逾期率的系数}\\ &\alpha,\beta&\geq 0&&\text{资方$j$逾期率服从Beta-Binomial分布的超参数}\\ &\sum\limits_{k=1}^{s} td_k &\leq 1&k=1,2,\ldots,q &\text{(f.) 所有业务类型承接订单占比之和≤1}\\ &\sum\limits_{j=1}^{m} d_j &\leq 1&j=1,2,\ldots,m &\text{(g.) 所有资方承接订单占比之和≤1}\\ &\Gamma({t\leq v_j})&\neq \emptyset, &j=1,2,\ldots,m &\text{截止当前时点$t$且在资方$j$授信有效期内,其承接订单的集合} \\ &x_{ij}&\in \{0,1\} &i=1,2,\ldots,n;j=1,2,\ldots,m &\text{用户$i$定向到资方$j$则取值为1,反之为0}\\ &\sum\limits_{j=1}^{m}x_{ij}&=1 &i=1,2,\ldots,n;j=1,2,\ldots,m &\text{(h.) 用户$i$最终只能选择一家资方}\\ &e(i)&=\left\{ \begin{array}{rcl} \frac{\frac{r_i}{12}\cdot (\frac{r_i}{12}+1)^{w_i}}{(1+\frac{r_i}{12})^{w_i}-1}\cdot w_i-1 & & {等额本息}\\ (w_i+1)*\frac{1}{2}*\frac{r_i}{12} & & {等额本金} \end{array} \right. ,&i=1,2,\ldots,n&\text{针对用户$i$的预期收益,有等额本息和等额本金两种方式}\\ &v_j&\geq0, &j=1,2,\ldots,m &\text{资方$j$授信有效期} \\ &s_j&\geq0, &j=1,2,\ldots,m &\text{资方$j$授信额度} \\ &m_i&\geq0, &i=1,2,\ldots,n &\text{用户$i$融资额为正整数,约看做EAD风险敞口} \\ &w_i&\geq0, &i=1,2,\ldots,n &\text{用户$i$融资期限,单位为月} \\ &t(i)&\geq0, &i=1,2,\ldots,n &\text{用户$i$所属业务类型} \\ &d_j&\geq0, &j=1,2,\ldots,m &\text{资方$j$承接订单占比为正浮点数} \\ &0\leq r_i&\leq1, &i=1,2,\ldots,n &\text{用户$i$匹配的金融产品方案对客年化利率} \\ &0\leq dr_j&\leq1, &j=1,2,\ldots,m &\text{资方$j$的可接受逾期率} \\ &0\leq p_j&\leq1, &j=1,2,\ldots,m &\text{资方$j$的通过率} \\ &c_j&\geq0, &j=1,2,\ldots,m &\text{资方$j$的资金成本} \\ &0\leq pd_i&\leq1, &i=1,2,\ldots,n &\text{用户$i$的预测违约概率} \\ &0\leq lgd_i&\leq1, &i=1,2,\ldots,n &\text{用户$i$融资资产的违约损失率,和车型处置损失有关} \\ &i&\geq0, &i=1,2,\ldots,n &\text{用户编号,截止目前一共有$n$位用户}\\ &j&\geq0, &j=1,2,\ldots,m &\text{资方编号,截止目前一共有$m$个资方}\\ &k&\geq0, &k=1,2,\ldots,q &\text{业务类型编号,截止目前一共有$q$个类型}\\ \end{array} \end{align*} \]
要点说明
1、每个用户的预期逾期率pd、预期损失率lgd需要实时拿到,背后要有风险模型、车辆处置回收模型支持,当然可简单做也可复杂做;
2、所有资方额度消耗采用基于当前时消耗实时计算的平滑消耗方式,平滑函数可设定,借鉴计算广告,可采用下面的累积指数函数;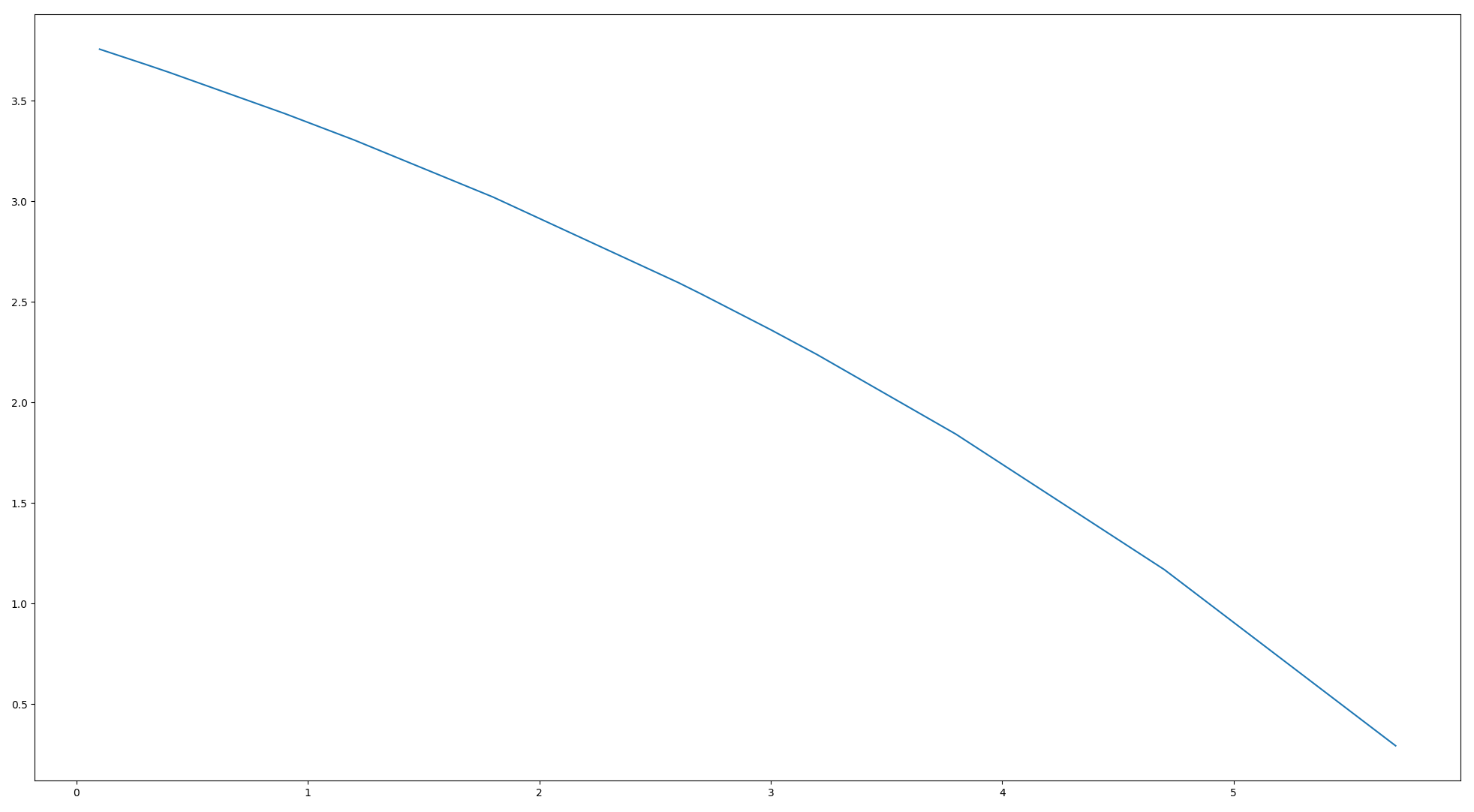
3、每家资方的额度有限,可以设定通过率高的资方优先被分配到订单;
4、可以对每种业务、每家资方做额度和单量的运营限制;
5、最优化目标函数需要包含以下项:做某个用户的精确或大致收益、做某个用户的pd(类似信用分)和lgd(基于资产残值的风险敞口或最坏情况下基于车辆融资额的风险敞口计算得到),做某个用户的资金成本、非预期损失如果可以获得那么也能加入;
6、由于不同资源方数据充分度不同,为了能算法出稳定的逾期率,采取平滑方式,引入\(beta\)分布,\(\alpha、\beta\)值的计算方法:
1)、假设1:用户信贷行为服从二项分布,其中参数\(I\)为信审通过,\(C\)为是否违约,\(pd\)为违约概率: \[ p(C_i|I_i,pd_i)=\begin{pmatrix} I_i \\ C_i \end{pmatrix}pd_i^{C_i}(1-pd_i)^{I_i-C_i} \]
2)、假设2:用户违约概率服从$ beta $分布: \[ \begin{align*} p(pd_i|\alpha,\beta)&=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}pd_i^{\alpha-1}(1-pd_i)^{\beta-1}\\ &=\frac{1}{B(\alpha,\beta)}pd_i^{\alpha-1}(1-pd_i)^{\beta-1} \end{align*} \]
3)、将用户违约概率视作隐含变量,则用户违约和它的联合概率分布为: \[ p(C_i,pd_i|I_i,\alpha,\beta)=p(C_i|pd_i,I_i)\cdot p(pd_i|\alpha,\beta) \]
4)、采用MLE去估计相关参数,假设有\(n\)个样本,则有: $ p(C,pd|I,,)=_{i=1}^np(C_i,pd_i|I_i,,) $
取\(ln\)后得完全数据的$ $: \[ \begin{align*} ln\text{ }p(C,pd|I,\alpha,\beta)&=\sum\limits_{i=1}^nln\text{ }p(C_i,pd_i|I_i,\alpha,\beta)\\ &=\sum\limits_{i=1}^nln\text{ }p(C_i|pd_i,I_i)+ln\text{ }p(pd_i|\alpha,\beta)\\ &=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}pd_i^{C_i}(1-pd_i)^{I_i-C_i}+ln\text{ }\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}pd_i^{\alpha-1}(1-pd_i)^{\beta-1}\\ &=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+C_iln\text{ }pd_i+(I_i-C_i)ln\text{ }(1-pd_i)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta)+(\alpha-1)ln\text{ }pd_i+(\beta-1)ln\text{ }(1-pd_i) \end{align*} \]
5)、如采用EM算法求解,需要计算完全数据的$ $的数学期望: \[ \begin{align*} E_{pd}ln\text{ }p(C,pd|I,\alpha,\beta) &=\sum\limits_{i=1}^nE_{pd}(ln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+C_iln\text{ }pd_i+(I_i-C_i)ln\text{ }(1-pd_i)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta)+(\alpha-1)ln\text{ }pd_i+(\beta-1)ln\text{ }(1-pd_i))\\ &=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+(C_i+\alpha-1)E_{pd}(ln\text{ }pd_i)+(I_i-C_i+\beta-1)E_{pd}(ln\text{ }(1-pd_i))\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta) \end{align*} \]
从式中可见,期望求解在于求得:$ E_{pd}(lnpd_i)) $ 以及 $ E_{pd}(ln(1-pd_i)) $ \[ \begin{align*} E_{pd}(ln\text{ }pd_i))&=\int_0^1ln\text{ }pd_i\cdot \frac{pd_i^{\alpha-1}(1-pd_i)^{\beta-1}}{B(\alpha,\beta)}d(pd_i)\\ &=\frac{1}{B(\alpha,\beta)}\int_0^1\frac{\partial pd_i^{\alpha-1}(1-pd_i)^{\beta-1}}{\partial \alpha}d(pd_i)\\ &=\frac{1}{B(\alpha,\beta)}\frac{\partial}{\partial \alpha}\int_0^1 pd_i^{\alpha-1}(1-pd_i)^{\beta-1}d(pd_i)\\ &=\frac{1}{B(\alpha,\beta)}\frac{\partial B(\alpha,\beta)}{\partial \alpha}\\ &=\frac{\partial ln \text{ }B(\alpha,\beta)}{\partial \alpha}\\ &=\frac{\partial ln\text{ }\Gamma(\alpha)}{\partial \alpha}-\frac{\partial ln\text{ }\Gamma(\alpha+\beta)}{\partial \alpha}\\ &=\psi(\alpha)-\psi(\alpha+\beta) \end{align*} \]
同理: $ E_{pd}(ln(1-pd_i))=()-(+) $ 因此,完全数据的$ $的数学期望最终为:
E-step: \[ \begin{align*} E_{pd}(ln\text{ }p(C,pd|I,\alpha,\beta))&=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+(C_i+\alpha-1)E_{pd}(ln\text{ }pd_i)+(I_i-C_i+\beta-1)E_{pd}(ln\text{ }(1-pd_i))\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta)\\ &=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+(C_i+\alpha-1)(\psi(\alpha)-\psi(\alpha+\beta)))+(I_i-C_i+\beta-1)(\psi(\beta)-\psi(\alpha+\beta)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta) \end{align*} \]
M-step: 求以上函数的极值,采用数学公式: $ NewtonRaphson $迭代法,得到: \[ \begin{align*} E_{pd}(ln\text{ }p(C,pd|I,\alpha,\beta))&=f(\alpha,\beta)\\ &=\sum\limits_{i=1}^nln\text{ }\begin{pmatrix} I_i \\ C_i \end{pmatrix}+(C_i+\alpha-1)(\psi(\alpha)-\psi(\alpha+\beta)))+(I_i-C_i+\beta-1)(\psi(\beta)-\psi(\alpha+\beta)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta) \end{align*} \]
于是: \[ \begin{align*} \frac{\partial f(\alpha,\beta)}{\partial \alpha} &=\frac{\partial}{\partial \alpha}\sum\limits_{i=1}^n(C_i+\alpha-1)\psi(\alpha)+(I_i-C_i+\beta-1)\psi(\beta)-(I_i+\alpha+\beta-2)\psi(\alpha+\beta)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta)\\ &=\sum\limits_{i=1}^n\psi(\alpha)+(C_i+\alpha-1)\psi_1(\alpha)-\psi(\alpha+\beta)-(I_i+\alpha+\beta-2)\psi_1(\alpha+\beta)+\psi(\alpha+\beta)-\psi(\alpha)\\ &=\sum\limits_{i=1}^n(C_i+\alpha-1)\psi_1(\alpha)-(I_i+\alpha+\beta-2)\psi_1(\alpha+\beta) \end{align*} \] \[ \begin{align*} \frac{\partial f(\alpha,\beta)}{\partial \beta} &=\frac{\partial}{\partial \beta}\sum\limits_{i=1}^n(C_i+\alpha-1)\psi(\alpha)+(I_i-C_i+\beta-1)\psi(\beta)-(I_i+\alpha+\beta-2)\psi(\alpha+\beta)\\ &+ln\text{ }\Gamma(\alpha+\beta)-ln\text{ }\Gamma(\alpha)-ln\text{ }\Gamma(\beta)\\ &=\sum\limits_{i=1}^n\psi(\beta)+(I_i-C_i+\beta-1)\psi_1(\beta)-\psi(\alpha+\beta)-(I_i+\alpha+\beta-2)\psi_1(\alpha+\beta)+\psi(\alpha+\beta)-\psi(\beta)\\ &=\sum\limits_{i=1}^n(I_i-C_i+\beta-1)\psi_1(\beta)-(I_i+\alpha+\beta-2)\psi_1(\alpha+\beta) \end{align*} \] 令: \[ \begin{align*} \frac{\partial f(\alpha,\beta)}{\partial \alpha}=0\\ \frac{\partial f(\alpha,\beta)}{\partial \beta}=0 \end{align*} \] 利用迭代式:$ x_{n+1}=x_n- $ 得到: \[ \alpha_{n+1}=\alpha_n-\frac{\sum\limits_{i=1}^n(C_i+\alpha_n-1)\psi_1(\alpha_n)-(I_i+\alpha_n+\beta_n-2)\psi_1(\alpha_n+\beta_n)}{\sum\limits_{i=1}^n\psi_1(\alpha_n)+(C_i+\alpha_n-1)\psi_2(\alpha_n)-\psi_1(\alpha_n+\beta_n)-(I_i+\alpha_n+\beta_n-2)\psi_2(\alpha_n+\beta_n)} \] \[ \beta_{n+1}=\beta_n-\frac{\sum\limits_{i=1}^n(I_i-C_i+\beta_n-1)\psi_1(\beta_n)-(I_i+\alpha_n+\beta_n-2)\psi_1(\alpha_n+\beta_n)}{\sum\limits_{i=1}^n\psi_1(\beta_n)+(I_i-C_i+\beta_n-1)\psi_2(\beta_n)-\psi_1(\alpha_n+\beta_n)-(I_i+\alpha_n+\beta_n-2)\psi_2(\alpha_n+\beta_n)} \]
例如:假设某资源方在某时间窗口做了6w单,其中100单发生逾期,则,平均逾期率为:0.17%,利用以上方法做平滑后,逾期率调整为0.23%, 其中: \(\alpha=1.61,\beta=682.85\),若今天线上来了该资源方的50个用户,他们的预测平均逾期率为:1.5%,则资源方当前逾期率为: \(r=1.58\%\cdot \lambda+0.23\%\cdot(1-\lambda)=0.3218\%\),其中: \(\lambda=\frac{50}{50+1.61+682.85}=0.068\)。
代码实践
完整代码可在这里获得,优化求解器采用Google的OR-Tools,关键代码如下:
1、构建二部图:
1 | from bitarray import bitarray |
2、构建最优化问题
1 | import math |
3、模拟实验
用户数据
1 | 用户10,融资额:76000,融资期限:36,业务类型:0,还款类型:0,融资利率:0.1188,违约概率率:0.0101,违约损失率:0.8,易鑫分:490.0,首付比例:0.1,已还款期数:0,匹配资方列表:[100, 200] |
资源方数据
1 | 资方100,授信额度:10.0,授信有效期:365,是否为循环额度:True,是否为托底资方:False,资方接受易鑫分下限:450.0,资方接受逾期率:0.012,预期资方单量占比:0.3,资方通过率:0.88,资金成本:0.103,alpha:50.0,beta:6500.0 |
初始二部图
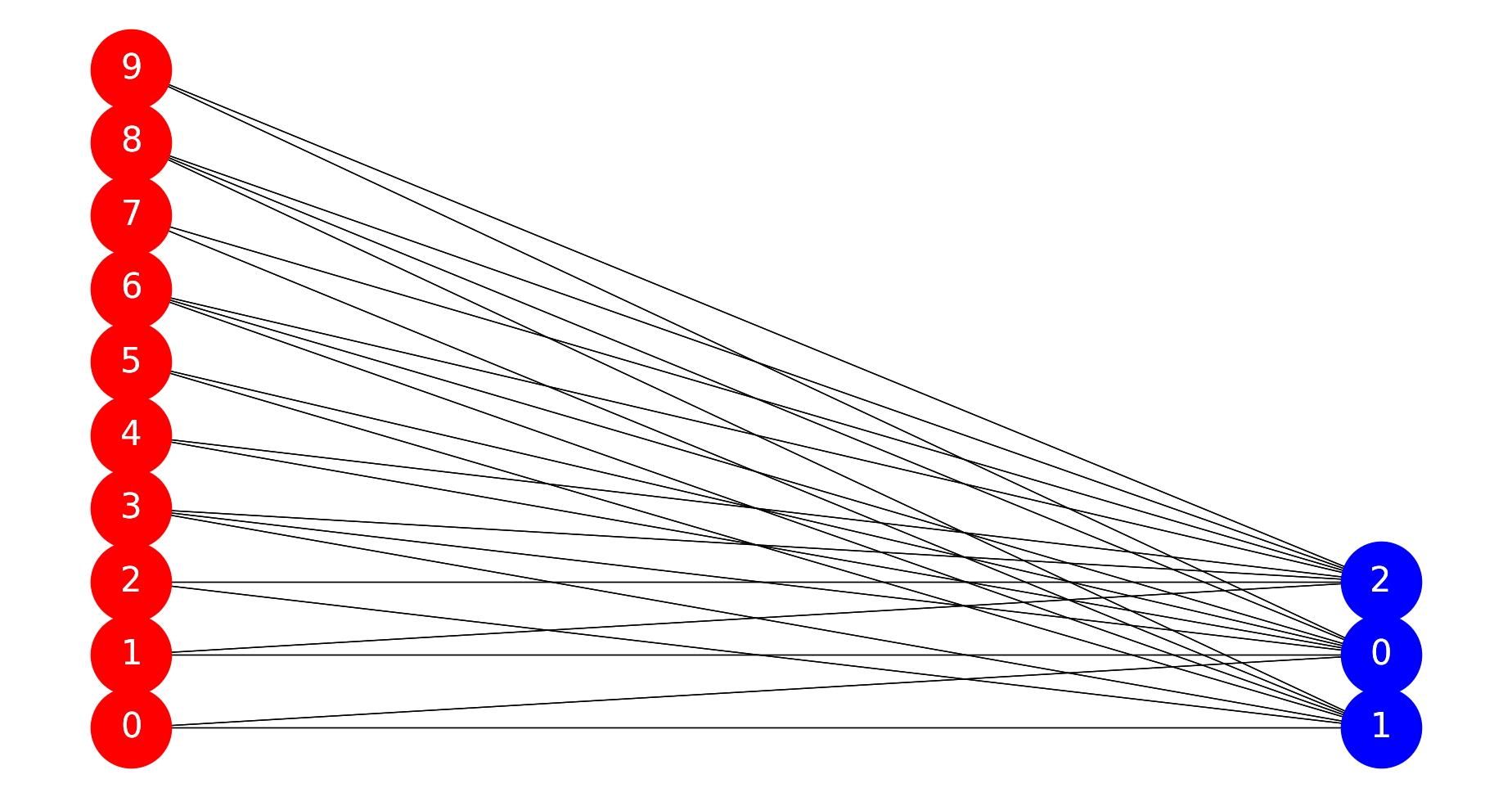
优化问题生成
1 | max (((((((((((((((((((((((6275.5393280828075 * x00) + (6047.5393280828075 * x01)) + (4375.031654669008 * x10)) + (5046.331654669008 * x12)) + (5444.143779111989 * x21)) + (6388.783779111988 * x22)) + (3535.9924397879054 * x30)) + (3358.9924397879054 * x31)) + (4114.192439787905 * x32)) + (20129.925959620494 * x40)) + (20948.225959620493 * x42)) + (6209.188139111804 * x50)) + (5920.588139111805 * x51)) + (5665.026587193259 * x60)) + (5451.726587193259 * x61)) + (6361.806587193259 * x62)) + (4148.304437444714 * x71)) + (5039.184437444714 * x72)) + (4197.370367470781 * x80)) + (4025.4703674707816 * x81)) + (4758.910367470781 * x82)) + (3492.406552072825 * x90)) + (3904.0065520728244 * x92)) |
优化求解结果
1 |
|