本文对BERTopic主题模型原理、思路和应用做了简单介绍。

BERTopic主题模型详解

主题模型是用来在非结构数据中无监督的发现隐含主题信息的一类重要工具，比较成熟和常用的算法有基于矩阵分解（如：SVD分解）的LSA（Latent Semantic Analysis）, 引入概率方法代替SVD的pLSA（Probabilistic Latent Semantic Analysis）, 贝叶斯版本的pLSA——LDA（Latent Dirichlet Allocation）。 但这类方法的本质是通过最小化误差从而找到能够复现原有文档分布的主题，对隐含语义的捕获能力非常有限（本质是对信息的distributional representation）， 而随着神经网络和Embedding技术（本质是对信息的distributed representation）的发展以及Transformer在NLP领域的爆发，出现了更加有趣的主题模型，其中Maarten Grootendorst提出的BERTopic是一个简洁而强大的算法，论文地址：《BERTopic: Neural topic modeling with a class-based TF-IDF procedure》。 本文代码示例可在这里访问。

BERTopic基本过程

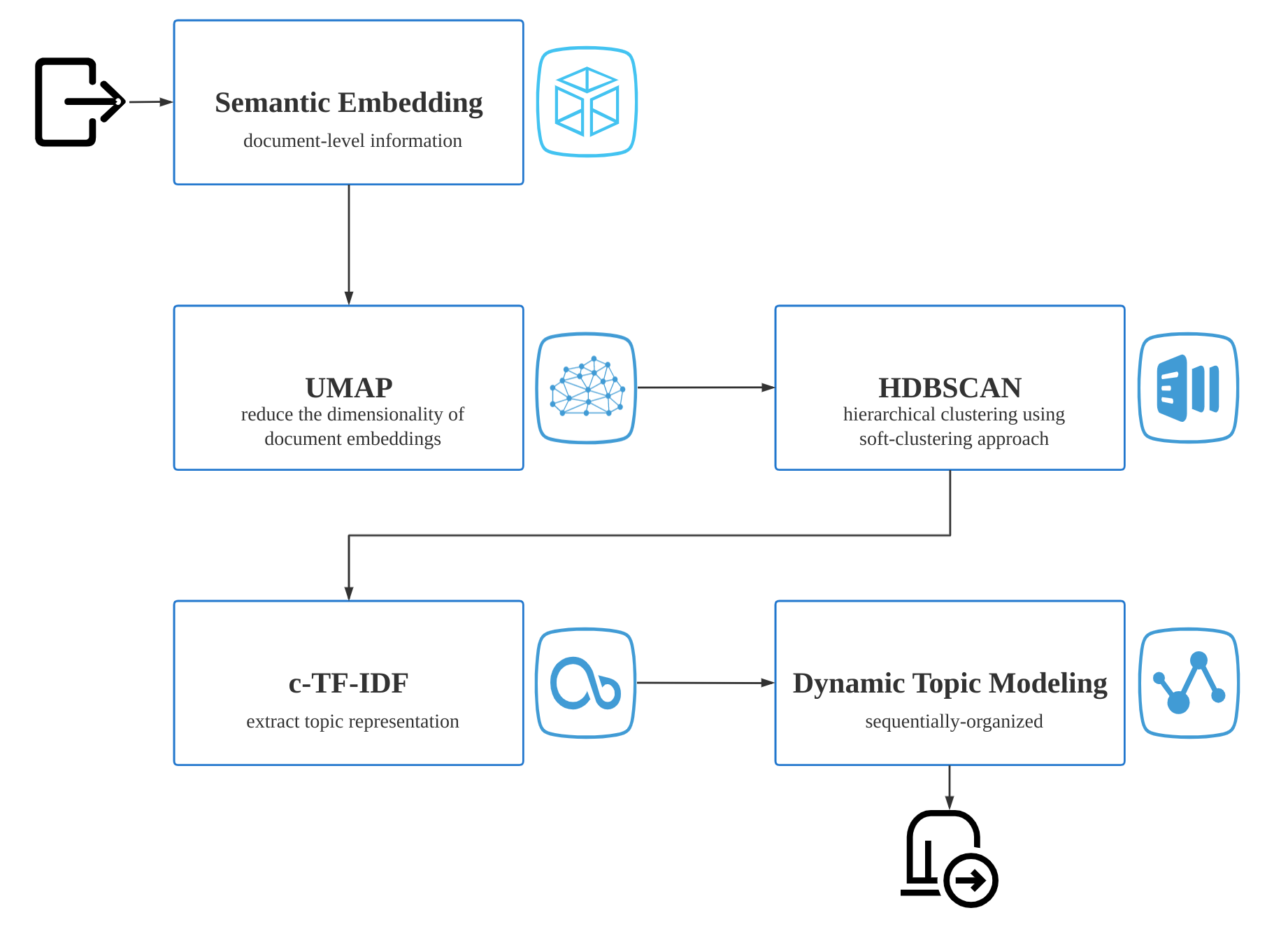
BERTopic由四大部分组成，如下图：

• 语义Embedding表示

• UMAP降维

• HDBSCAN文本聚类

• c-TF-IDF主题生成

语义Embedding

记得当初word2vec刚出现时，我对其惊艳的表现印象很深刻（经典例子：king-man+women=queen），随后出现了类似的sentence2vec、doc2vec应用于不同粒度，不过本质都是通过distributed representation生成信息的语义空间，在这个空间中，可以用“距离”来衡量任意两个稠密向量的“语义”相似度， 生成Embedding向量又有几类方法，例如：基于当前段落向量和上下文向量去预测目标词或基于段落向量去预测上下文词 和 基于Transformer结构的算法（如：Bert），而后者的效果是非常明显的，相比传统类似BOW（Bag of words）的方法，基于Transformer结构的算法同时考虑了上下文信息和词序以及句子中所有词之间的相关性。 对于BERTopic，语义Embedding是第一步也是最重要的一步，语义表达的效果直接决定了后续主题生成的效果。

BERTopic支持以下几种embedding model的库：

• Sentence Transformers

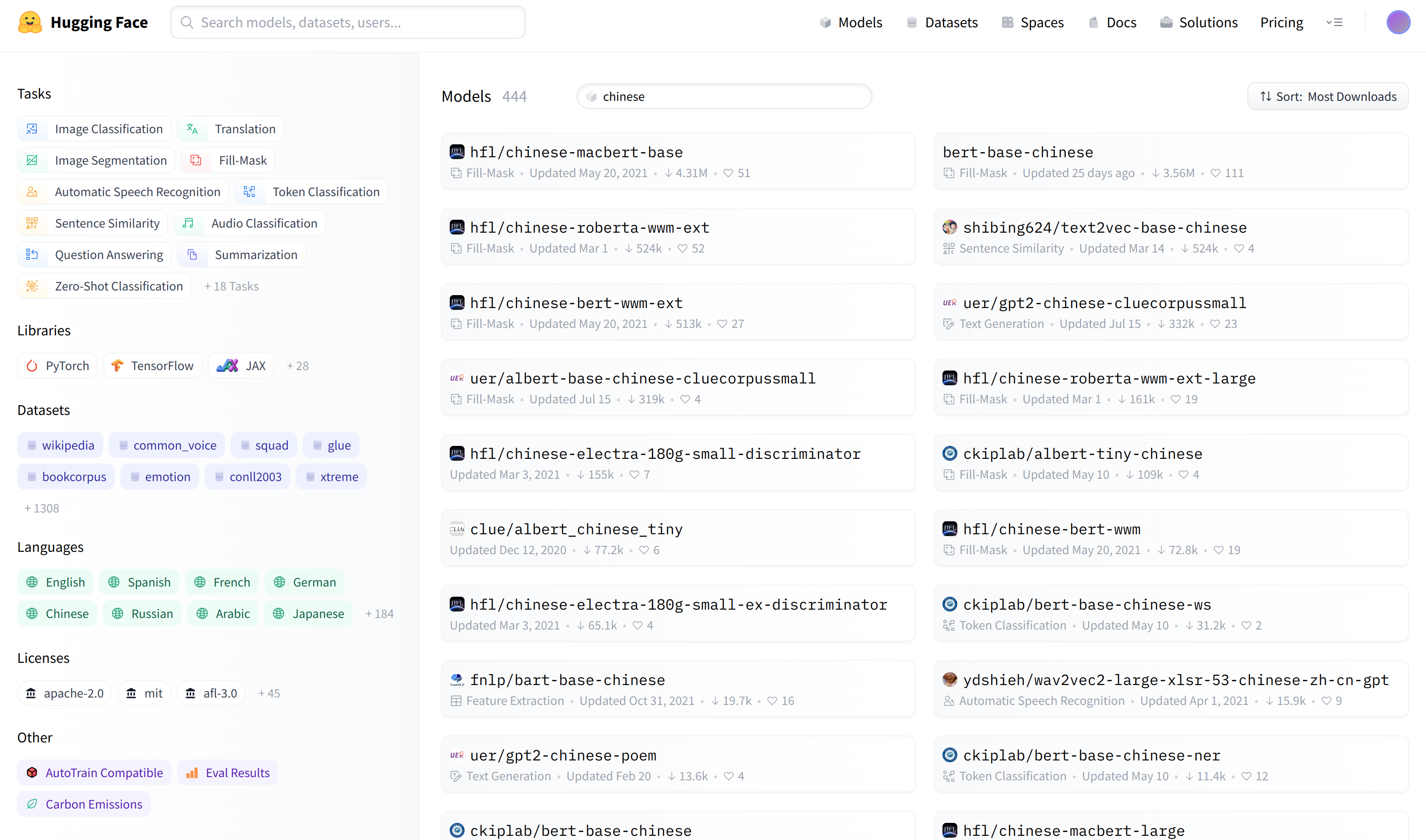
  基于PyTorch和HugingFace Transformers项目的Python库，使用非常方便，只需要在 https://huggingface.co 上选择合适的模型就可开箱即用，例如：

  

  import torch
  import torch.nn.functional as F
  from sentence_transformers import SentenceTransformer
  
  sentences = ["我这边是易鑫集团的工作人员", "办理流程就比较简单了?", "裸车价多少钱呢？", "加一下您微信"]
  
  model = SentenceTransformer('shibing624/text2vec-base-chinese')
  embeddings = torch.from_numpy(model.encode(sentences))
  
  cand = embeddings[0]
  print(sentences[0])
  
  for i in range(1, len(embeddings)):
      print('——', sentences[i], '相关度:', F.cosine_similarity(cand, embeddings[i], dim=0))

  /usr/bin/python /home/dell/PycharmProjects/BERTopic/test.py
  2022-08-16 12:25:46.384364: I tensorflow/core/util/util.cc:169] oneDNN custom operations are on. You may see slightly different numerical results due to floating-point round-off errors from different computation orders. To turn them off, set the environment variable `TF_ENABLE_ONEDNN_OPTS=0`.
  Asking to truncate to max_length but no maximum length is provided and the model has no predefined maximum length. Default to no truncation.
  tensor([[-0.1795, -0.7887,  1.3699,  ..., -0.3907, -0.1538,  0.1391],
          [-0.7942, -0.1645,  0.8701,  ..., -0.9783, -0.2415,  0.0278],
          [-0.7666,  0.4602, -0.0598,  ..., -0.6351, -0.8215,  0.2701],
          [ 0.5862,  0.3013,  0.7182,  ..., -0.3796, -0.0490, -0.5745]])
  我这边是易鑫集团的工作人员
  —— 办理流程就比较简单了? 相似度: tensor(0.5054)
  —— 裸车价多少钱呢？ 相似度: tensor(0.3580)
  —— 加一下您微信 相似度: tensor(0.4324)
  
  Process finished with exit code 0

• Flair

• SpaCy

    import spacy
  
    sentences = ["我这边是易鑫集团的工作人员", "办理流程就比较简单了?", "裸车价多少钱呢？", "加一下您微信"]
    print(sentences[0])
  
    nlp = spacy.load("zh_core_web_sm")
    doc = [nlp(s) for s in sentences]With what we have so far, if we want to correctly project close distances between points, the moderate distances are distorted and appear as huge distances in the low dimensional space. According to the authors of t-SNE, this is because “the area of the two-dimensional map that is available to accommodate moderately distant data points will not be nearly large enough compared with the area available to accommodate nearby data points.”
  
  To solve this, the second main modification introduced is the use of the Student t-Distribution (which is what gives the ‘t’ to t-SNE) with one degree of freedom for the low-dimensional probabilities,
  
  
    for i in range(1, len(doc)):
        print('——', sentences[i], '相关度:', doc[0].similarity(doc[i]))

  /usr/bin/python /home/dell/PycharmProjects/BERTopic/test.py
  2022-08-16 16:24:57.076178: I tensorflow/core/util/util.cc:169] oneDNN custom operations are on. You may see slightly different numerical results due to floating-point round-off errors from different computation orders. To turn them off, set the environment variable `TF_ENABLE_ONEDNN_OPTS=0`.
  我这边是易鑫集团的工作人员
  —— 办理流程就比较简单了? 相关度: -0.023583169329516124
  —— 裸车价多少钱呢？ 相关度: 0.19299579633898184
  —— 加一下您微信 相关度: -0.01393847136393582
  
  Process finished with exit code 0

• Gensim

• USE (TF Hub)

降维

当文本信息被embedding后，每个文档会成为一个高维（通常是几百维以上）稠密向量，但整个语义空间会很稀疏，逻辑上语义相关的文档会因为“距离”接近在空间内“聚集”，而为了识别主题向量，首先想到的是基于密度的聚类算法，但这类算法对向量维度很敏感，维度越高速度越慢，所以有必要把原来几百维的向量压缩降维到个位数维度，比如2~3维，同时也方便数据可视化。 降维方法主要有三类：特征选择法（ Feature Selection），基于矩阵分解的方法如PCA（Principal Component Analysis）、SVD（Singular Value Decomposition）等以及基于邻居图（Neighbor Graphs）的方法SNE（Stochastic Neighbor Embedding）、t-SNE（t-Distributed Stochastic Neighbourh Embedding）、UMAP（Uniform Manifold Approximation and Projection）等，其中UMAP更是速度和效果方面的佼佼者。

邻居图方法大致可以看做以下几个步骤：

• 定义和计算输入空间数据概率分布\(p\)

• 定义和计算降维空间数据概率分布\(q\)

• 定义损失函数，描述以上两个概率分布的差异

• 由于这种映射会损失信息，所以最小化求解损失函数，找到让两个分布最接近的参数

• 多次实验找到较优的困惑度（Perplexity）参数 困惑度指的是：已知当前点为\(x_i\)，计算概率分布时需要选取的领域内包含的节点个数，显然其物理含义是：取值越大，领域越大，越可能将远处的点作为邻居节点，越能具有“全局”视野但越容易误判，反之越能保留更“准确”的局部信息但容易切得太细，“全局”视野差，困惑度选多少没有理论最优值，但可以通过自己或别人的实验找到比较好的经验值。

比较下几种邻居图方法：

• SNE 1、定义和计算输入空间数据概率分布\(p\)

  假设当前点为\(x_i=x_0\)，困惑度取值为\(n\)，则其邻居节点为\(x_j \in \{x_1,...,x_n\}\)，节点\(i\)与其任一邻居节点的距离采用缩放的欧氏距离：\(d_{j|i}=\sqrt{\frac{||x_i-x_j||^2}{2\delta_i^2}}\)（其中\(\delta_i\)为调节参数），任一邻居节点\(j\)的分布为：\[p_{j|i}=\frac{e^{-d_{j|i}^2}}{\sum\limits_{k=1,k\neq i}^ne^{-d_{k|i}^2}}\] 注意，为了满足用户设定的困惑度参数\(n\)，算法需要通过调节参数\(\delta_i\)（假设以\(x_i\)为中心的高斯分布的方差）来实现，这样使得\(p_{j|i}\neq p_{i|j}\)，即不满足对称性。 另外由于没法用唯一的\(\delta_i\)值应用于所有\(x_i\)，所以用户在指定困惑度后，SNE采用binary search确定，因此困惑度定义为：\[Perp(P_i)=2^{H(P_i)}=2^{-\sum\limits_jp_{j|i}log_2{p(j|i)}}\] 于是算法通过自动调整\(\delta_i\)参数使得困惑度等于用户设定的值。 ps：困惑度的经验值为5~50。

  2.定义和计算降维空间数据概率分布\(q\)

  假设输入空间中的点\(x_i\)和\(x_j\)映射到降维空间中的点为\(y_i\)和\(y_j\)，则任一邻居节点\(j\)的分布为：\[q_{j|i}=\frac{e^{-||y_i-y_j||^2}}{\sum\limits_{k=1,k\neq i}^ne^{-||y_i-y_k||^2}}\]

  3.定义损失函数

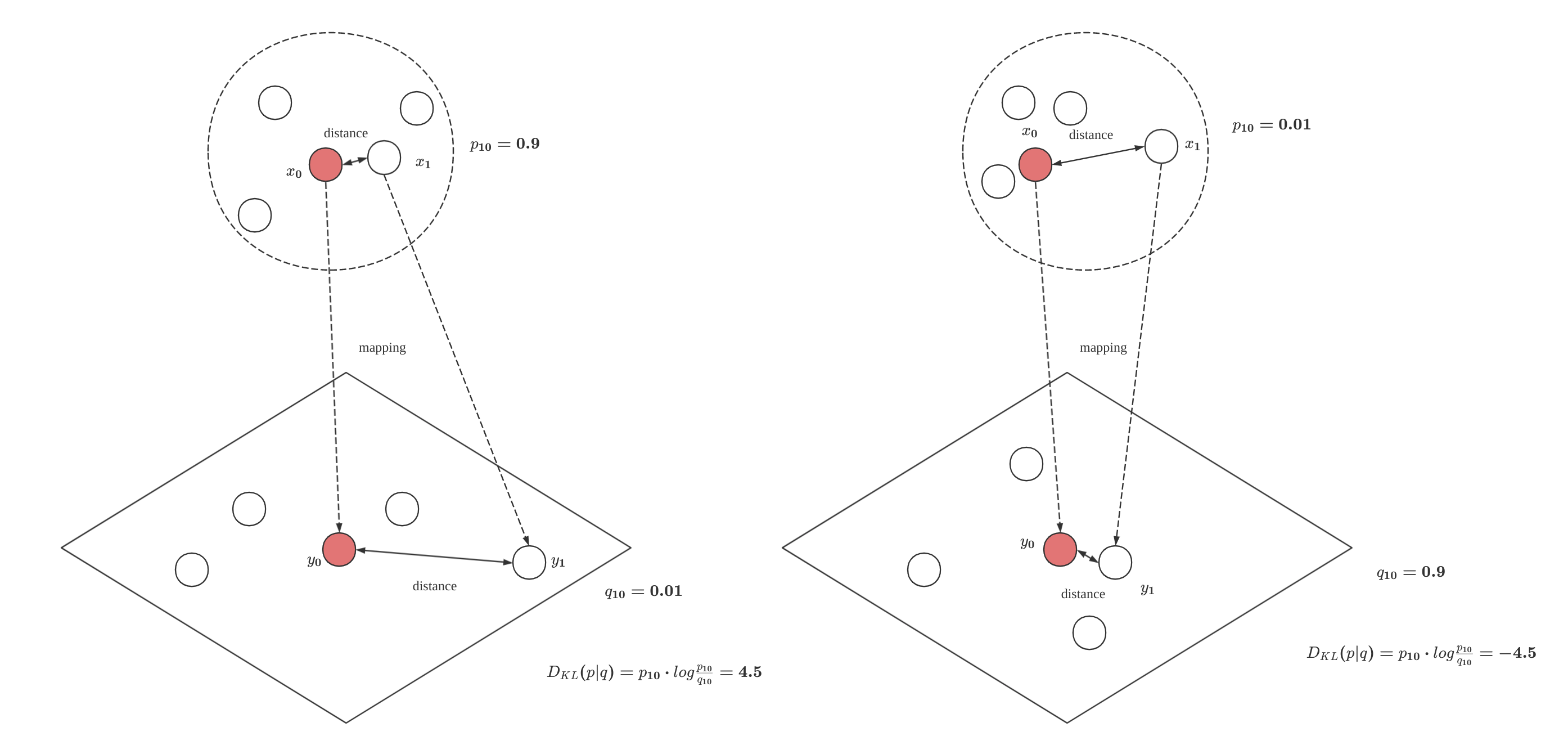
  直观上看，如果数据从高维输入空间映射到降维空间后的信息损失很小，那么两个概率分布应该在“距离”上很接近，一个自然的选择是KL散度（KL Divergence）：\[D_{​KL}(p∣∣q)=\sum\limits_{i=1}^m\sum\limits_{j=1}^n p(j|i)⋅log​\frac{p(j|i)}{q(j​|i)}\] 不过这个损失函数也有明显缺点，如下图：

  

  当高维空间中两个距离相近的点降维映射后距离变远了，此时损失函数会做比较大的惩罚，但当高维空间中两个距离较远的点降维映射后距离变近了，则此时并没有多大惩罚。

  4.求解

  \(min D_{​KL}(p∣∣q)\)，采用梯度下降求解，损失函数梯度如下： \[ \frac{\partial D_{​KL}(p∣∣q)}{\partial y_i}=2\sum\limits_{j=1}^{n}(p(j|i)-q(j|i)+p(i|j)-q(i|j))(y_i-y_j) \] 采用动量梯度下降，迭代式如下： \[ y_t=y_{t-1}+\eta\frac{\partial D_{​KL}(p∣∣q)}{\partial y}+\alpha(t)(y_{t-1}-y_{t-2}) \] 其中\(\eta\)为学习率，\(\alpha\)为第\(t\)次迭代时的动量值（用来尽可能不陷入到局部最小值），优化求解过程比较费劲，对初始值很敏感，且需要在数据集上多次训练才有可能找到合适的超参数。

• t-SNE 从SNE原理上看，除了损失函数优化求解费劲外，还有个缺陷是降维后的数据拥挤问题（Crowding Problem），为了解决这两个问题，做了以下改进： 1、输入空间的条件概率分布改为联合概率分布，使其具有对称性

  \(i\)是\(j\)的邻居，反过来也成立，即\[p(ij) =\frac{p(j|i)+p(i|j)}{2n}\]

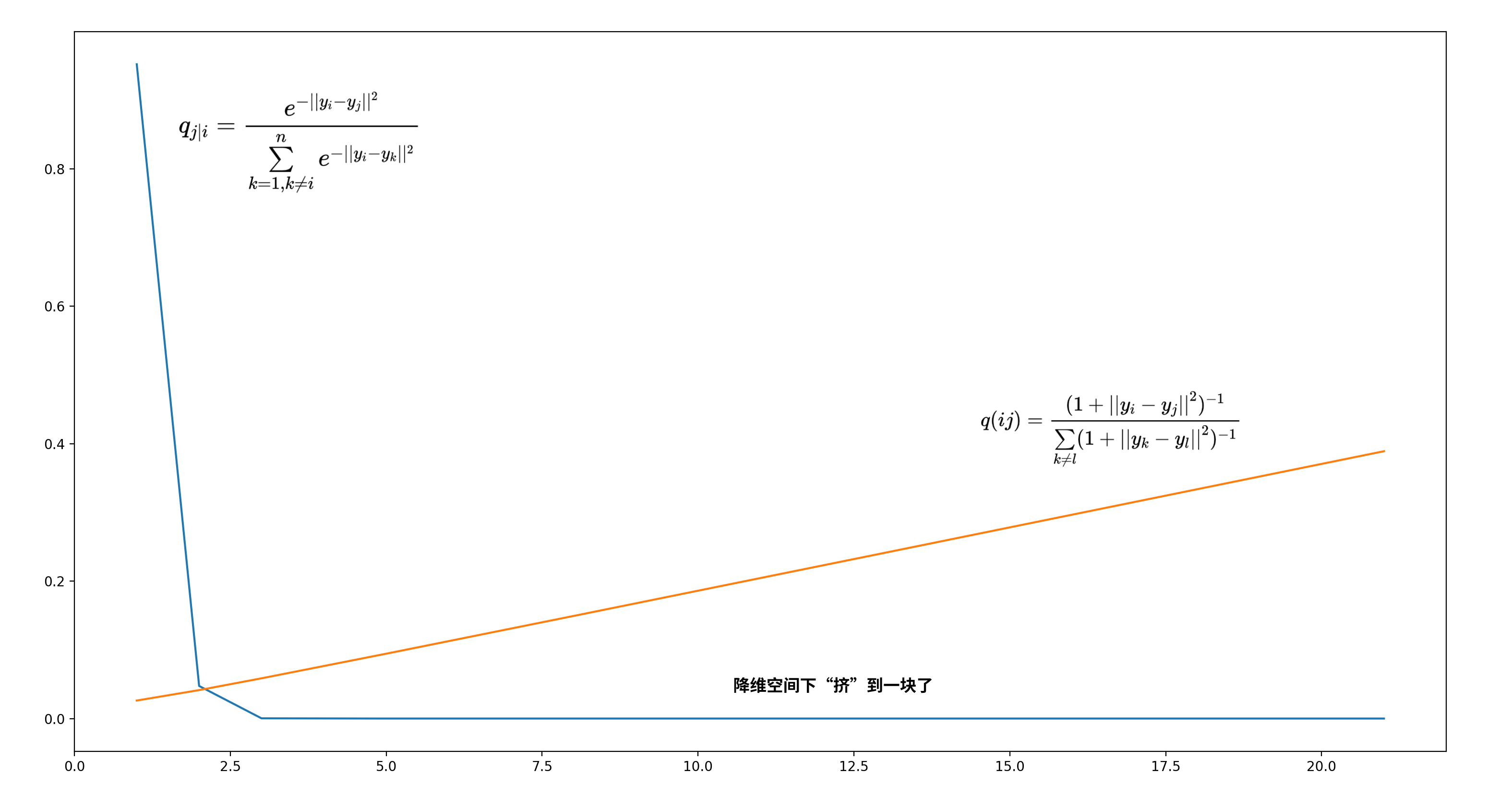
  2、解决降维后的数据拥挤问题 简单说，高维空间中的点尤其是互相之间距离中等或较远的点，在降维后出现的聚集现象叫做数据拥挤问题。 t-SNE另外一个改进是对降维后空间数据做自由度为1的t分布假设：\(f(x)=\frac{1}{\pi(1+x^2)}\)，这样联合概率分布\(q(ij)\)就变成： \[q(ij)=\frac{(1+||y_i-y_j||^2)^{-1}}{\sum\limits_{k\neq l}(1+||y_k-y_l||^2)^{-1}}\] 因为\(p(ij)=p(ji),q(ij)=q(ji)\)，所以损失函数变成了： \[D_{​KL}(p∣∣q)=\sum\limits_{i=1}^m\sum\limits_{j=1}^n p(ij)⋅log​\frac{p(ij)}{q(ij)}\] 求梯度时就简单多了，变成： \[ \frac{\partial D_{​KL}(p∣∣q)}{\partial y_i}=4\sum\limits_{j=1}^{n}(p(ij)-q(ij))(y_i-y_j) \]

  直观比较如图：

  

  横坐标是降维后两点间距离，纵坐标是\(q\)值，显然以高斯分布为假设的数据，对距离远的映射后\(p\)值都聚集在一起了，反观以t分布为假设的数据则更有区分度。

• UMAP UMAP的理论基础基于黎曼几何和代数拓扑的框架，理论基础很完备。相比t-SNE，它并未做概率分布假设，而是直接定义相似度，而且保留了更多的全局结构信息，对embedding的维度没有计算上的限制，内存占用更小、运行速度更快，是降维领域的SOTA算法。

  什么是“流形”（manifold）： 流形是一个数学上抽象的拓扑空间，这个空间是n维的，其中的每个点局部来看都有一个类似欧几里得空间的邻域（例如：一维流形中每个点都有一个类似一条线段的邻域，二维流形中每个点都有一个类似圆盘的邻域，三维流形中，每个点都有一个类似单位圆球\(x^2+y^2=1\)的邻域），但全局结构又可能很复杂（典型的例子：地球的结构，局部看是平的，但全局看是个球体），流形的定义使得人们可以用更容易理解的简单空间的属性来表达和理解更复杂的结构（换个角度看，流形可以视做欧式空间的非线性推广）。 流形还常常被赋予一些附加结构，例如它可以是平滑的（Smooth Manifolds）的可微流形、可以定义距离和角度的黎曼流形（Riemannian Manifold）等等。

  UMAP的算法设计在数据上做了以下假设：

  1、数据在黎曼流形上服从均匀分布，黎曼流形的特点有：可定义距离和角度、流形是可微的

  2、流形是局部连接的(locally connected)，这样拓扑空间就能保证将局部计算结果合理地、光滑地拼接起来，从而揭示出整体结构

  3、黎曼度量（在流形上定义距离的方法，由流形的切空间中所有点的內积组成，是一个对称正定矩阵）是局部恒定（locally constant，上述矩阵是常数对称矩阵）的

  以流形中的任何一个输入数据点\(X_i\)为中心，在给定体积的球形邻域内包含的输入数据点个数大致相当，也就是说，以流形中的任何一个输入数据点\(X_i\)为中心的球形邻域内，如果都包含\(k\)个邻居节点，那么这些球形邻域的体积应该大致相同，因而可以利用\(X_i\)到其第\(k\)个最近邻的距离对\(X_i\)到其邻居们的距离做归一化从而近似得到\(X_i\)到其邻居的测地线距离。 \(k\)的大小决定了我们希望在多大程度上局部地估计黎曼度量，即\(k\)越小代表我们越想捕捉到局部结构信息，反之亦然。 基于以上假设的流形学习，就是要根据已知的数据样本通过学习高维流形的内在结构或规律，找出嵌入在高维空间中的低维光滑流形，从而揭示隐含在高维数据空间中的内在的低维空间结构，整体是一个非线性降维过程，但带来的问题是可解释性会比较差，另外由于UMAP更关注对局部信息的准确表达，所以如果全局结构更重要那么就要谨慎选择了。

  原理说明：

  1、定义和计算输入空间数据概率分布p

  条件概率分布定义为： \[p(i|j)=e^{\frac{-\max(0,d(x_i,x_j)-\rho_i)}{\sigma_i}}\] 以上的计算只需要输入节点的\(n\)个邻居节点（这也是UMAP比t-SNE高效的地方之一），其中: \(d(x_i,x_j)\)为两点间距离且不一定得是欧氏距离， \(\rho_i\)是与\(x_i\)距离最近的邻居节点的距离，即： \[\rho_i=\min(d(x_i,x_j)|1\leq j\leq k,d(x_i,x_j)>0)\] \(\sigma_i\)是与t-SNE中\(\delta_i\)有类似作用的调节参数，为了满足用户设定的困惑度，由以下式子得到： \[ \sum\limits_{j=1}^k e^{\frac{-\max(0,d(x_i,x_j)-\rho_i)}{\sigma_i}}=log_2k \]

  联合概率分布定义为： \[p(ij)=p(i|j)+p(j|i)-p(i|j)p(j|i)\]

  2.定义和计算降维空间数据概率分布q

  联合概率分布定义为： \[q(ij)=(1+a||y_i-y_j||_2^{2b})^{-1}\] 其中a、b为大于0的超参数，默认可取：\(a\approx1.93,b\approx0.79\)

  3.定义损失函数 使用交叉熵为损失函数，定义如下： \[ C_{UMAP} =\sum\limits_{i\neq j}p(ij)log\frac{p(ij)}{q(ij)}+(1-p(ij))log\frac{1-p(ij)}{1-q(ij)} \]

  实现标准库

  UMAP有官方实现的标准库，说明如下：https://umap-learn.readthedocs.io/en/latest/，几个核心超参数含义：

  1、n_neighbors

  上面公式中的参数\(k\)，用来tradeoff局部结构信息和全局结构信息，取值越小，越注重局部结构信息，取值范围[2,200]，默认最佳实践为15。

  2、min_dist

  控制降维后空间中点之间的紧密程度，取值越大，越保留数据原有拓扑结构，它的取值会影响上述公式中\(a,b\)的值，取值范围[0.0,0.99]，默认最佳实践为0.1。

  3、n_components 整数值，用于设定降维空间的维度，取值范围[2,100]，为方便可视化，可以取2或3。

  此外metric参数用于指定距离公式，支持23种距离，为了让每次降维后结果都一样，需要给参数random_state赋值。

  一个手写体数字识别的例子：

  from sklearn.datasets import load_digits
  import umap.plot
  import matplotlib.pyplot as plt
  
  # 利用sklearn直接导入手写体数据集.
  digits = load_digits()
  # 打印部分数据集以便直观查看.
  f, a = plt.subplots(15, 15)
  axes = a.flatten()
  for i, item in enumerate(axes):
      item.imshow(digits.images[i], cmap='gray')
  
  plt.setp(axes, xticks=[], yticks=[], frame_on=False)
  plt.tight_layout(h_pad=0.05, w_pad=0.02)
  
  # UMAP降维.
  mapper = umap.UMAP(n_neighbors=15,
                     n_components=2,
                     min_dist=0.1,
                     random_state=2022).fit(digits.data)
  # 可视化降维结果.
  q = umap.plot.points(mapper, labels=digits.target)
  umap.plot.show(q)

  原始数据集如下，包含0~9的10种手写体数据：

  

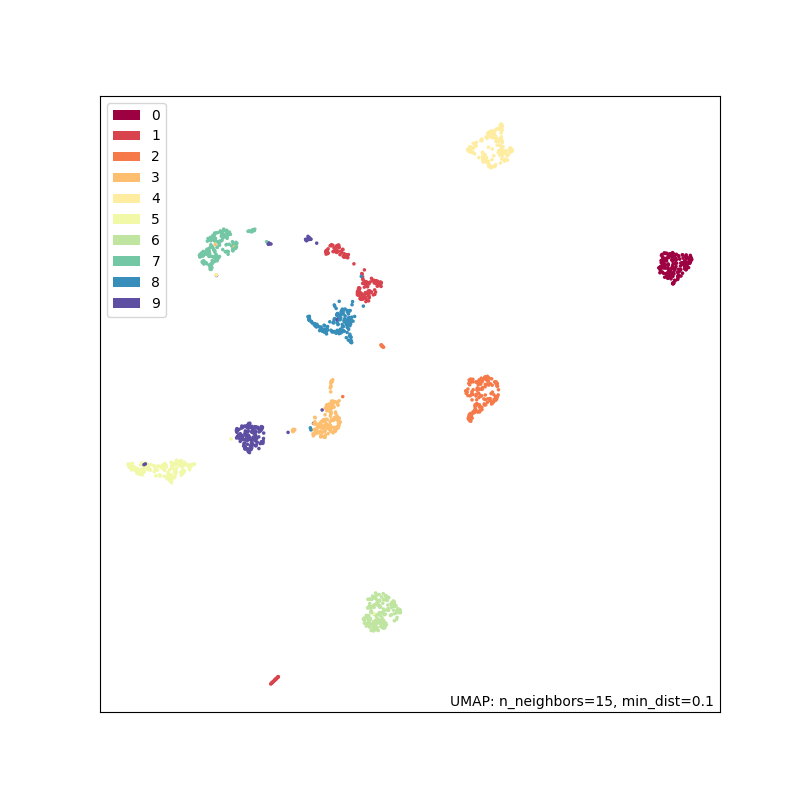
  降维结果如下：

  

  可以看到，相同的手写体数字在降维后大部分会聚在一起。

HDBSCAN聚类

降维算法是无监督学习，所以通过UMAP实际得到的应该如下图：

接下来就需要用聚类算法尽可能的把数据中高内聚低耦合的规律找出来，聚类算法大致分为基于扁平或层次结构的聚类和基于质心或密度的聚类，当然两类也可以交叉。扁平聚类可以看做层次聚类的特例，它们有点像决策树，更关注层次关系，典型的例子是：“国家->省->市->县...”这种层次关系的发现， 质心聚类更关注找到每个以质心为中心的“球状”的聚类，密度聚类则可以处理不规则形状的聚类。如果结合密度聚类和层次聚类，就可以得到既能处理不规则形状又能得到解释性比较好还能方便识别异常点的聚类算法，HDBSCAN（Hierarchical Density-Based Spatial Clustering of Applications with Noise）就是一个这类算法。

还以digits数据集为例，UMAP降维后接着做HDBSCAN聚类，代码如下：

from sklearn.datasets import load_digits
import umap.plot
import matplotlib.pyplot as plt
import hdbscan
import seaborn as sns

digits = load_digits()

mapper = umap.UMAP(n_neighbors=15,
                   n_components=2,
                   min_dist=0.1,
                   random_state=2022).fit_transform(digits.data)

clusterer = hdbscan.HDBSCAN(min_cluster_size=15,
                            metric='manhattan',
                            cluster_selection_method='eom',
                            prediction_data=True)
clusterer.fit(mapper)

ids = {}
for x in clusterer.labels_:
    if x not in ids.keys():
        ids[x] = 1

color_palette = sns.color_palette('bright', len(ids))

cluster_colors = [color_palette[x] if x >= 0
                  else (0.5, 0.5, 0.5)
                  for x in clusterer.labels_]
cluster_member_colors = [sns.desaturate(x, p) for x, p in
                         zip(cluster_colors, clusterer.probabilities_)]

plt.scatter(mapper[:, 0], mapper[:, 1], s=50, linewidth=0, c=cluster_member_colors, alpha=0.25)
plt.show()

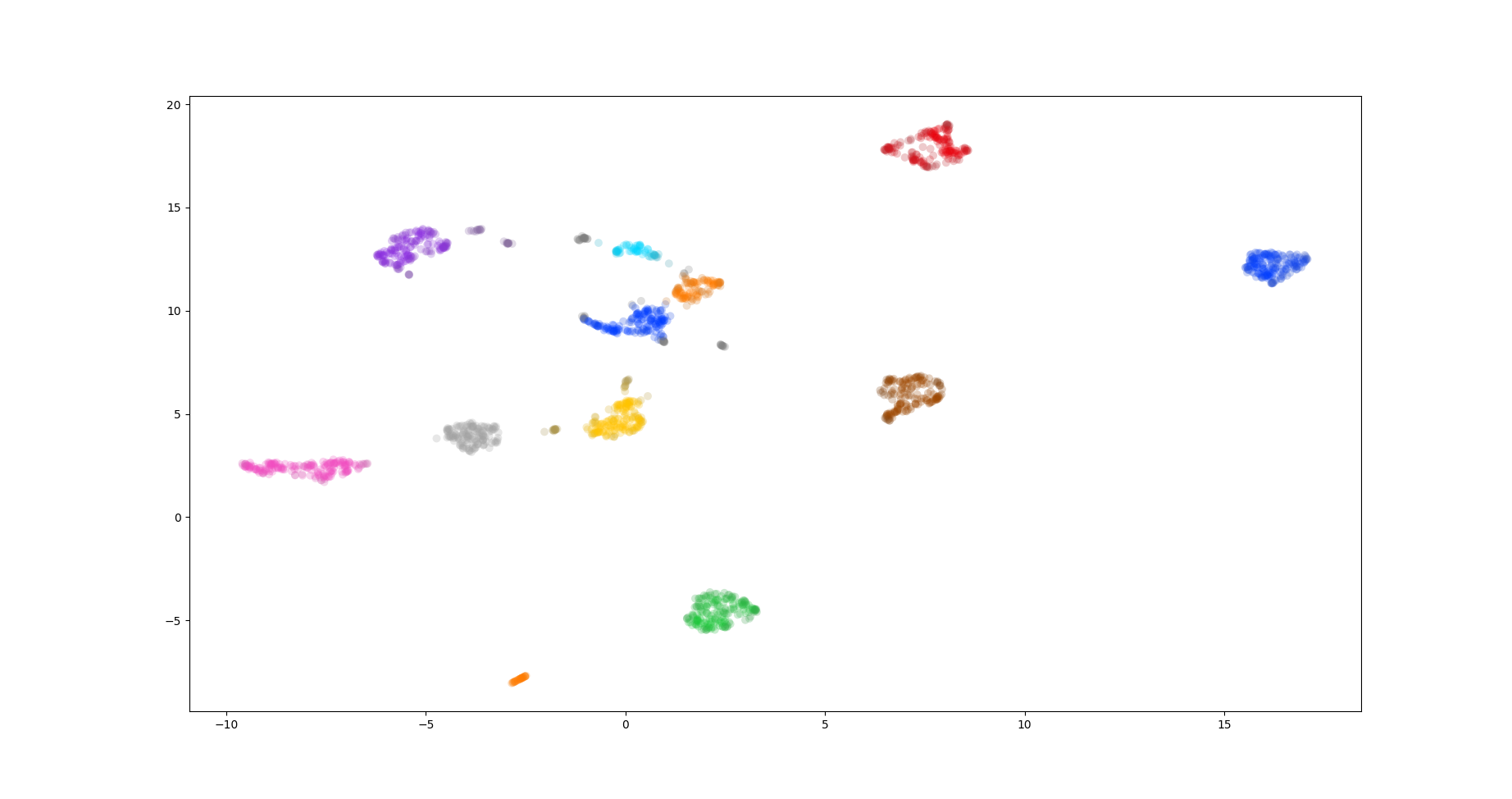
按照不同聚类id着色后如下：

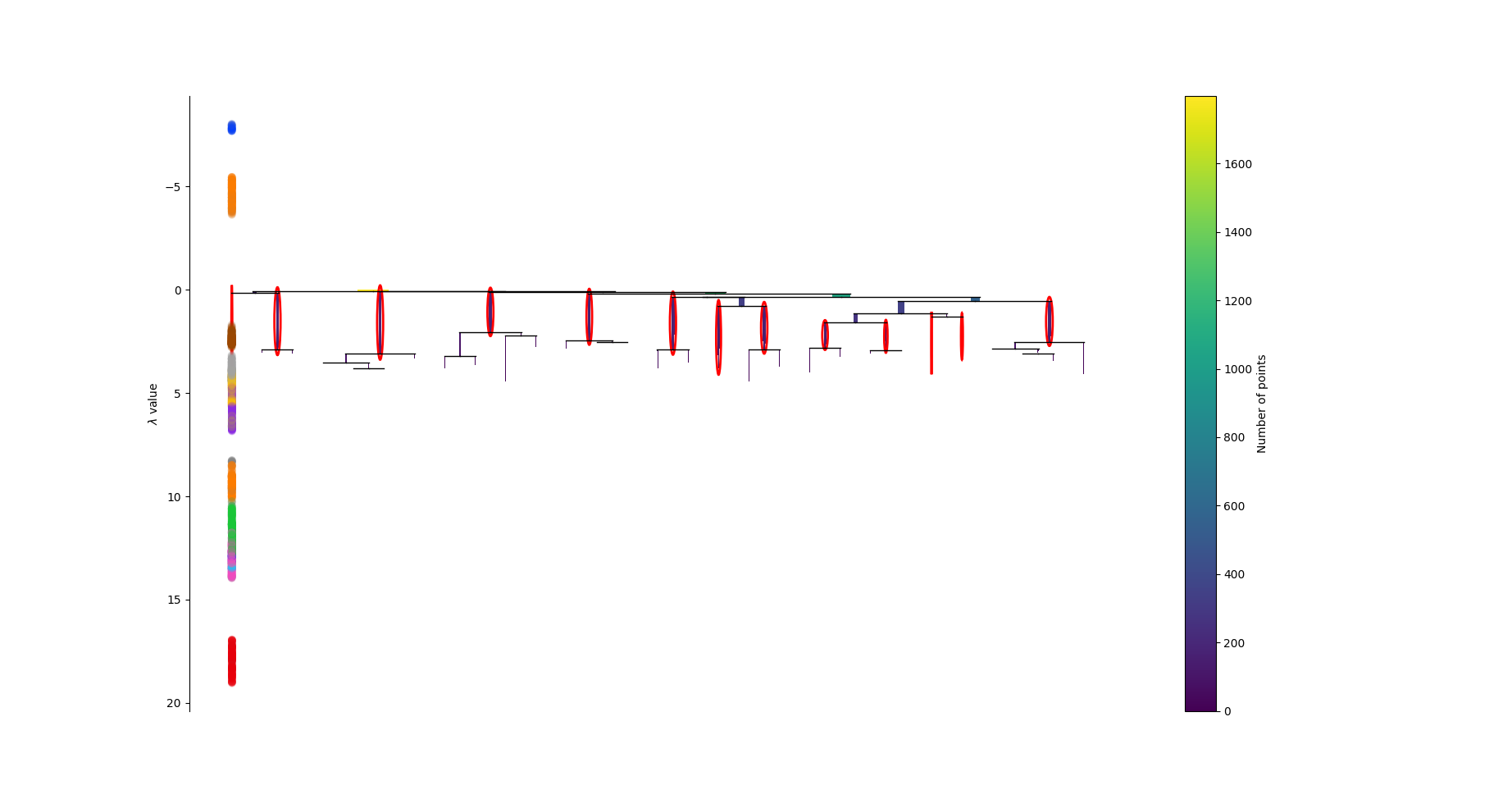
层次结构如下：

HDBSCAN的数据假设

所有机器学习算法背后都有假设，甚至所有方法背后都有假设，基于这些假设方法才有效，HDBSCAN对数据做了以下假设：

1、数据聚集簇（cluster）的形状不规则，有扁的、有长条的（如前面的digits数据集）

2、簇的大小不一，有的胖有的瘦

3、簇的密度不一，有的稠密，有的稀疏

4、存在噪声点

5、数据分布可以看做是多个不同概率分布的叠加

基于密度的聚类

怎么理解基于密度的聚类呢？举个例子：假设数据服从某个二元高斯分布\(f\)，它的数据散点图和高斯分布的pdf关系如图：

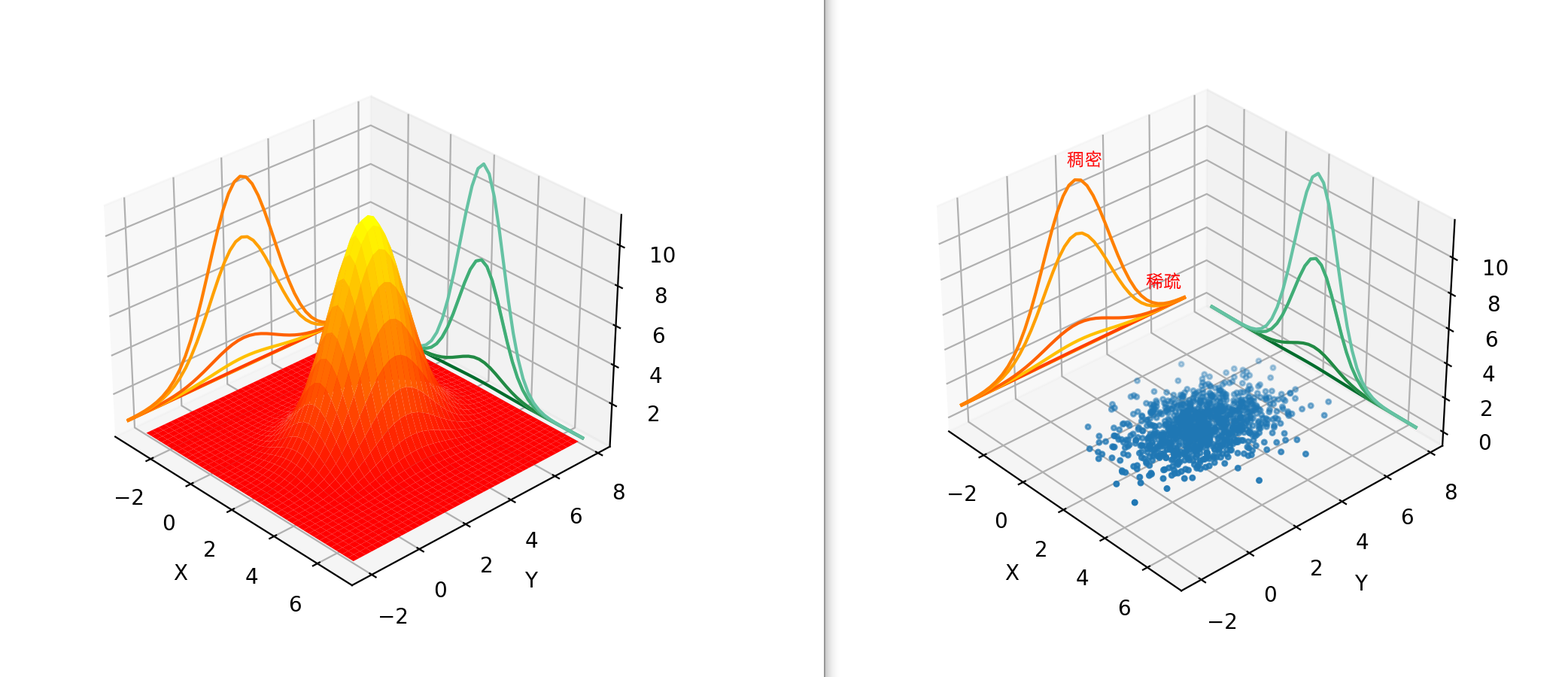
如果把每个维度投影，可以看到边缘分布是高斯分布，它的“山峰”处的数据比较稠密，反之“山谷”处的数据比较稀疏，同时pdf中概率越大的地方对应的散点图区域越稠密。 可以推广到数据有多个“山峰”和多个“山谷”，例如以下数据集\(A\)，由三个高斯分布叠加生成：

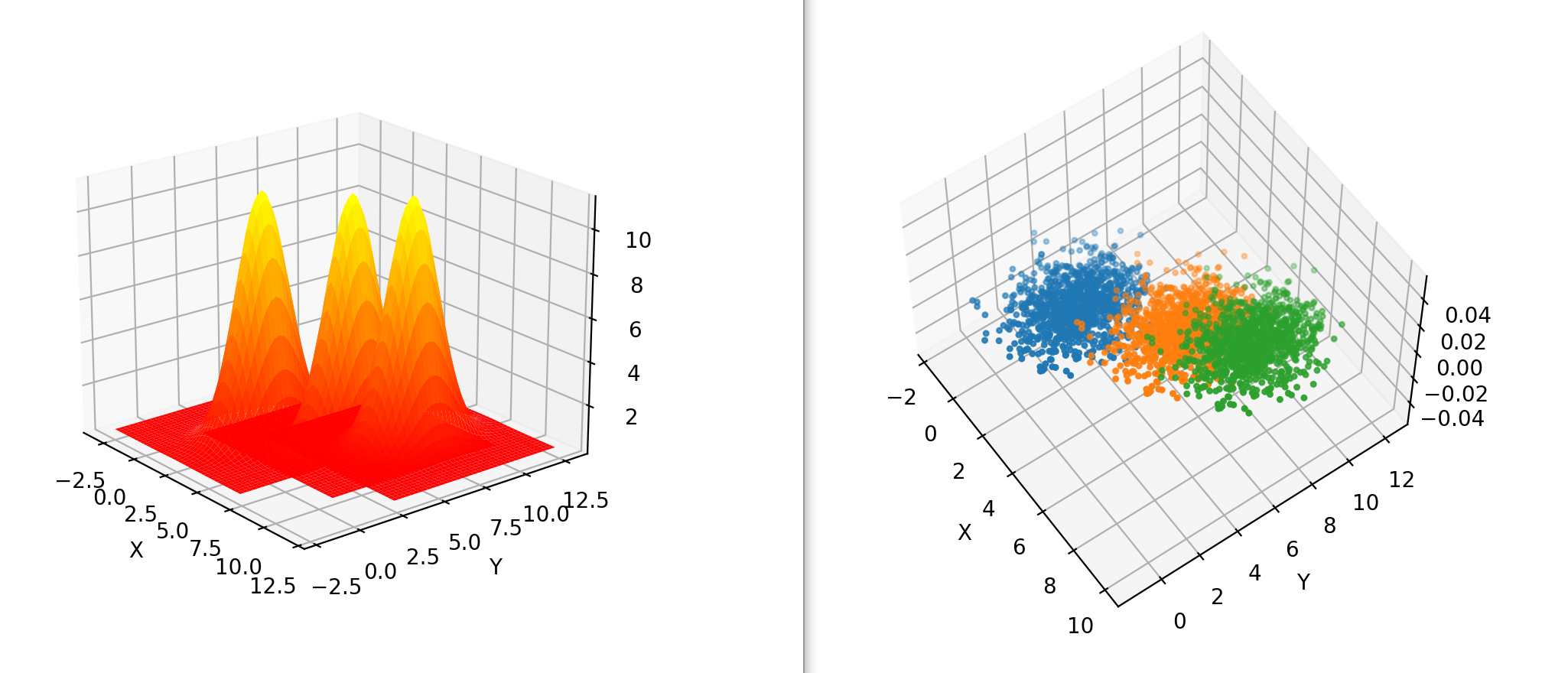
基于密度的聚类就是把这些“山谷”找出来作为边界，从而得到若干个相对独立的“山头”。

层次密度聚类

假设数据分布为\(f\)，我们需要一个阈值\(\lambda\)来确定到底应该聚几类，如图：

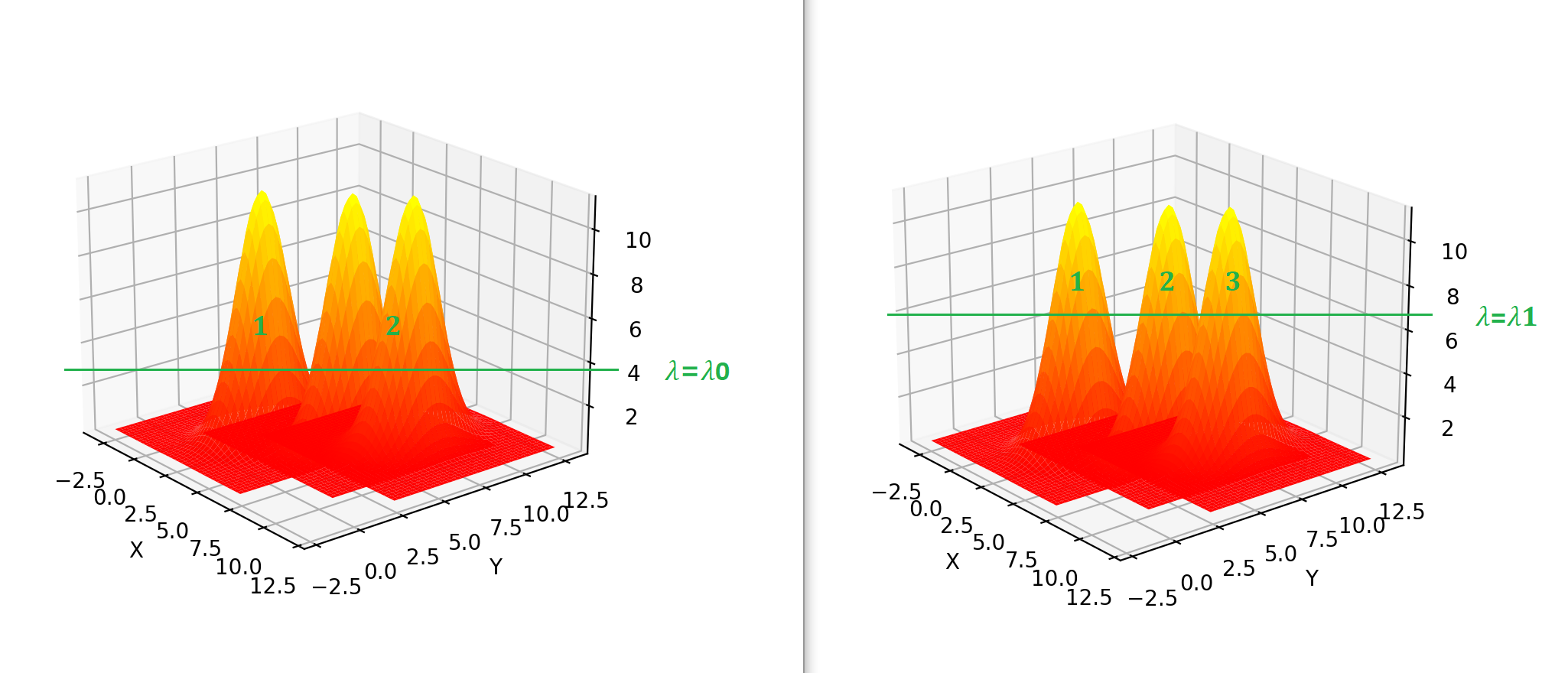
当\(\lambda=\lambda_0\)时，数据被聚成2类，当\(\lambda=\lambda_1\)时则是3类，\(\lambda\)是聚类的超参数，那么怎么确定这个值呢？《Accelerated Hierarchical Density Clustering》一文介绍了一种叫eom（excess of mass）的算法，大致原理如下：

1、excess of mass值定义为：\[E(C,\lambda) = \int_{C_λ}(f(x) − \lambda)dx\] 其中\(C\)为\(f\)域的子集：$ C_{} = {x C | f(x) λ}$。

2、当以\(λ_{C_i}\)作为阈值划分出类簇\(C_i\)时，如果\(λ_{min}(C_i)\)为能够划分出\(C_i\)这个类簇的最小阈值时，它的eom定义为： \[ E(C_i) = \int_{C_i}(f(x) − \lambda_{min}(C_i))dx \]

3、如果\(λ_{max}(C_i)\)为能够划分出\(C_i\)这个类簇的最大阈值，则定义其reom（relative excess of mass）值为： \[ E_R(C_i) = \int_{C_i}(min(f(x),λ_{max}(C_i)) − λ_{min}(C_i))dx \]

如果\(C_i\)有多个子树\(C_{i_1},C_{i_2},C_{i_3},...,C_{i_k}\)，则reom值为： \[ E_R(C_i) = E(C_i) −\sum\limits_{j=1}^kE(C_{i_j}) \]

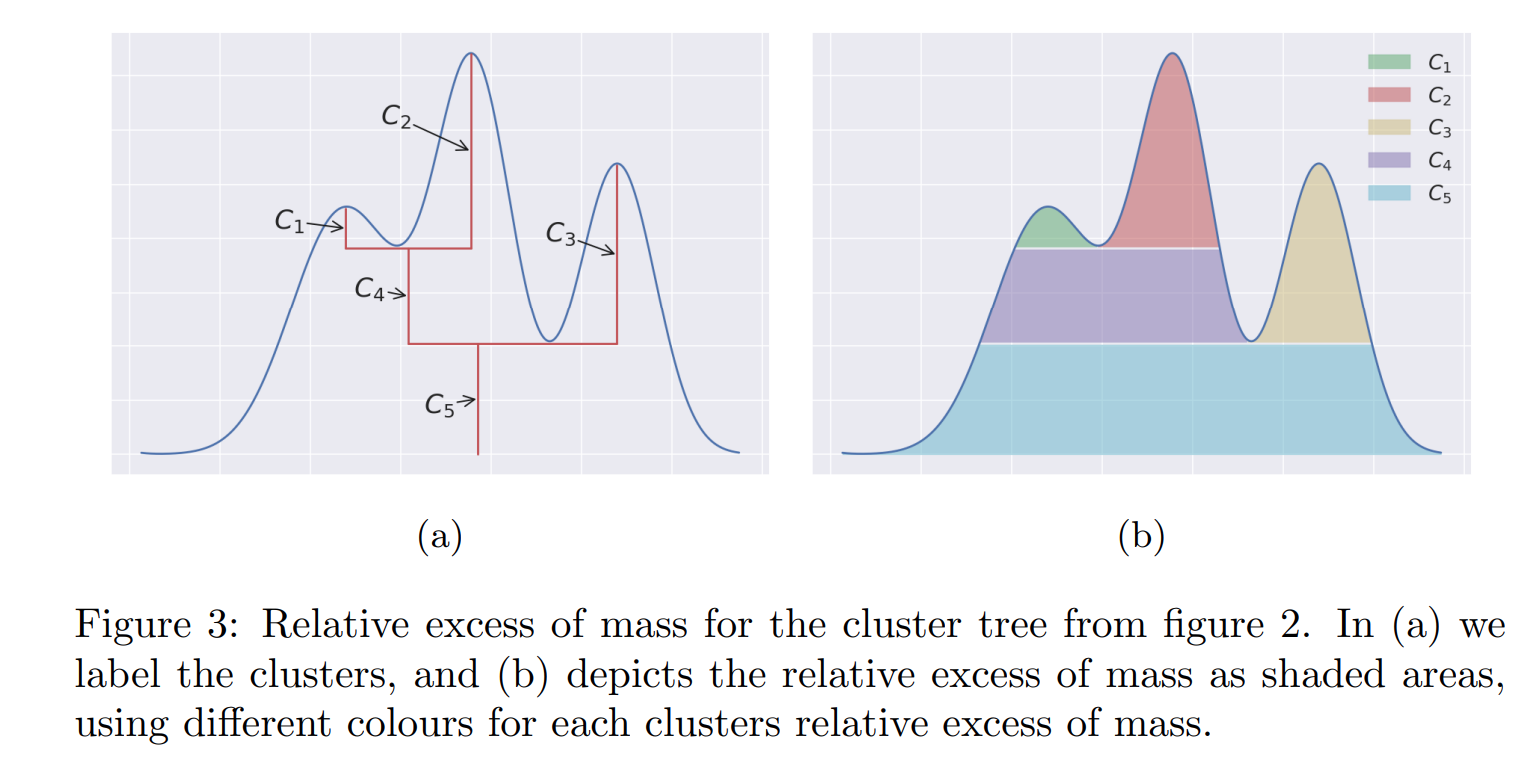
由于真实数据的pdf函数\(f\)是未知的，所以需要通过已有数据做经验密度估计，方法简单描述如下： 对任何一个点\(j\)，以\(\epsilon\)为半径画“圆/球”邻域，数下里面包含的邻居节点个数，个数越多，意味着此处越稠密，对应的pdf值越大，反之亦然。 反过来换个角度，假设指定\(k\)近邻的参数\(k=k_0\)，找到某点\(j\)可以包含\(k_0\)个邻居节点的最小的“圆/球”邻域，那么这个半径\(\epsilon_{x_j}\)就可以作为pdf的估计，所以可以定义\(f(x_j)\)的经验pdf为： \[ \hat{f}(x_j)=\frac{1}{\epsilon_{x_j}} \]

由于此时经验分布是离散的，所以上述eom改写为： \[ E(C_i) = \sum\limits_{x_j\in C_i}(\hat{f}(x_j) − \lambda_{min}(C_i)) \]

reom为： \[ \sigma(C_i) = E(C_i) −\sum\limits_{j=1}^kE(C_{i_j}) \]

最后求解一个让所有类簇的reom之和最大的约束最优化问题即可，即： \[ \begin{eqnarray} max&\sum\limits_{i\in \{1,2,...,n\}} \sigma(C_i) & \\ s.t.&C_i \cap C_j=\emptyset &\quad where \quad i\neq j \end{eqnarray} \]

详情可以参考论文《Hierarchical density estimates for data clustering, visualization, and outlier detection》。

层次结构示意：

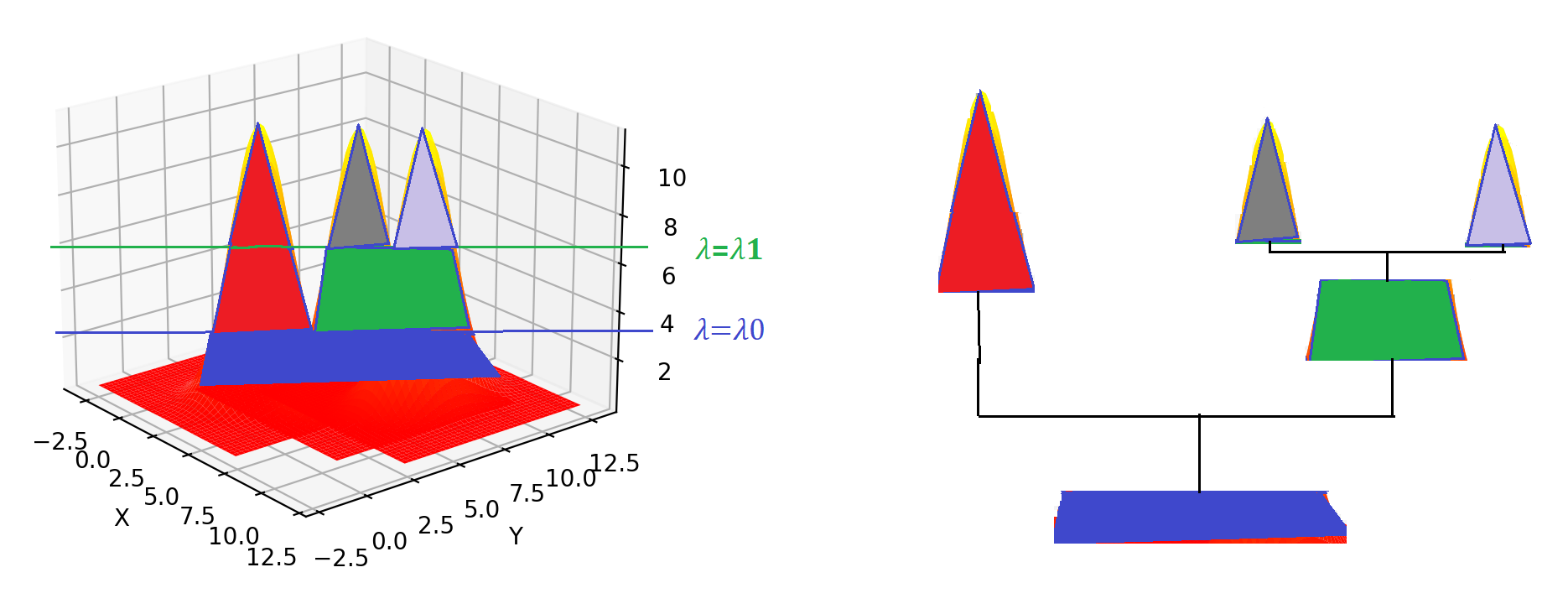
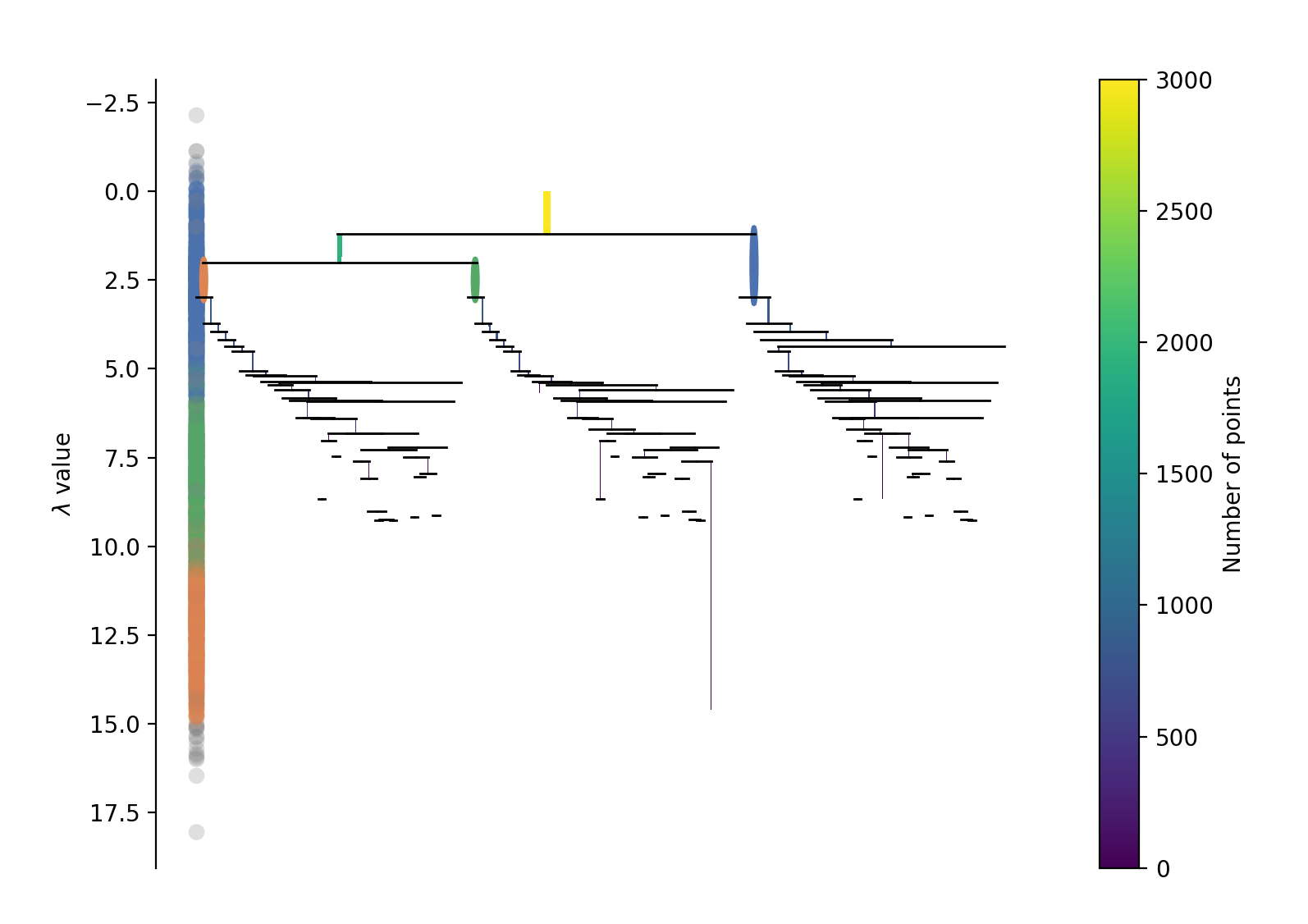
使用HDBSCAN的库可以方便的完成以上过程，数据集\(A\)的层次聚类如下：

主题标题生成

主题标题生成采用改进的TF-IDF算法（c-TF-IDF），作为比较，原本的TF-IDF算法如下： \[ W_{t,d}=tf_{t,d}\cdot \log(\frac{N}{df_t}) \] 其中，\(tf_{t,d}\)是词\(t\)在文档\(d\)中的词频，\(df_t\)是词\(t\)出现在多少的文档中，\(N\)是总文档数。

c-TF-IDF算法如下： \[ W_{t,c}=tf_{t,c}\cdot \log(1+\frac{A}{tf_t}) \] 其中，所有属于类簇\(c\)的文档被看做一个大文档，\(tf_{t,c}\)是词\(t\)在这个大文档中的词频，\(tf_t\)是词\(t\)出现在多少个类簇中，\(A\)是所有类簇的平均单词数量（即单词总数/类簇个数，注意，为了让\(\log\)函数结果是正数，所以需要加个1），最后，对每个类簇，选出权重最高的top n个词作为该主题的标题。

BERTopic代码实践

以搜狐新闻为语料做简单演示，核心类如下，完整代码在这里：

class CCTopic:
    def __init__(self,
                 embedding_model_name: str = 'DMetaSoul/sbert-chinese-general-v2-distill',
                 backend: str = 'sentence_transformers',
                 min_topic_size=10,
                 nr_topics=None,
                 threshold: float = 0.015
                 ):
        # 'paraphrase-distilroberta-base-v1'
        # 'DMetaSoul/sbert-chinese-general-v2-distill'
        # 使用开箱即用的预训练模型，也可根据自有数据做fine-tuning.
        if backend == 'sentence_transformers':
            self.embedding_model = SentenceTransformer(embedding_model_name)
        elif backend == 'pretrained':
            self.tokenizer = BertTokenizer.from_pretrained(embedding_model_name)
            self.embedding_model = BertModel.from_pretrained(embedding_model_name)

        self.min_topic_size = min_topic_size
        self.topic_threshold = threshold
        self.documents = None
        self.topic_model = None
        self.topic_probs = None
        self.topics = None
        self.nr_topics = nr_topics

    def fit_model(self, doc_path='data/dx_txt/all1_cut.dat', save_path='models/distill.dat'):
        self.documents = fetch_corpus(doc_path)
        stable_umap = UMAP(n_neighbors=15,
                           n_components=5,
                           min_dist=0.0,
                           metric='cosine',
                           random_state=2022)

        self.topic_model = BERTopic(language="chinese (simplified)",
                                    min_topic_size=self.min_topic_size,
                                    umap_model=stable_umap,
                                    calculate_probabilities=True,
                                    nr_topics=self.nr_topics,
                                    verbose=True)

        s_embeddings = None
        try:
            s_embeddings = self.embedding_model.encode(self.documents, show_progress_bar=True)
        except:
            print(self.documents)

        logger.info('Begin training...')
        self.topics, self.topic_probs = self.topic_model.fit_transform(self.documents, s_embeddings)
        logger.info('End training.')
        logger.info(self.topic_model.get_topic_info())

        # 生成主题对应的标题文档
        topics_docs = pd.DataFrame({'topic': self.topics, 'doc': self.documents})
        topics_docs.to_excel('topic.xlsx')

        self.topic_model.save(save_path)

    def visualize(self, n):
        bar_chart = self.topic_model.visualize_barchart(top_n_topics=300)
        bar_chart.write_html('figures/bar_chart.html')
        logger.info(self.topic_model.get_topic(10))

        first_new_topic_probs = self.topic_model.visualize_distribution(self.topic_probs[n], min_probability=0)
        logger.info('document content ' + self.documents[n])
        first_new_topic_probs.write_html('figures/first_new_topic_probs.html')

        visualize_topics1 = self.topic_model.visualize_topics()
        # 可视化结果保存至html中，可以动态显示信息
        visualize_topics1.write_html('figures/distance.html')

        visualize_hierarchy = self.topic_model.visualize_hierarchy()
        visualize_hierarchy.write_html('figures/hierarchy.html')

    def inference(self, docs, topn=5, min_probability=0.00, model_path='models/distill.dat'):
        if self.topic_model is None:
            self.topic_model = BERTopic.load(model_path)

        can_embeddings = self.embedding_model.encode(docs)
        topics, probs = self.topic_model.transform(docs, can_embeddings)
        vis_probs = self.topic_model.visualize_distribution(probs[0], min_probability=min_probability)
        vis_probs.write_html('figures/vis_probs.html')

        self.topic_threshold = 0
        selected_topics = np.argwhere(probs[0] >= self.topic_threshold).flatten()

        if topn >= len(selected_topics) > 0:
            cut_probs = probs[0][selected_topics]
        else:
            selected_topics = np.argpartition(probs[0], -topn, axis=None)[-topn:]
            cut_probs = probs[0][selected_topics]

        selected_topics = selected_topics[np.argsort(-cut_probs)]

        return topics, [(self.topic_model.topic_names[t], probs[0][t]) for t in selected_topics]

BERTopic库可视化方面很丰富，展示几个常用的：

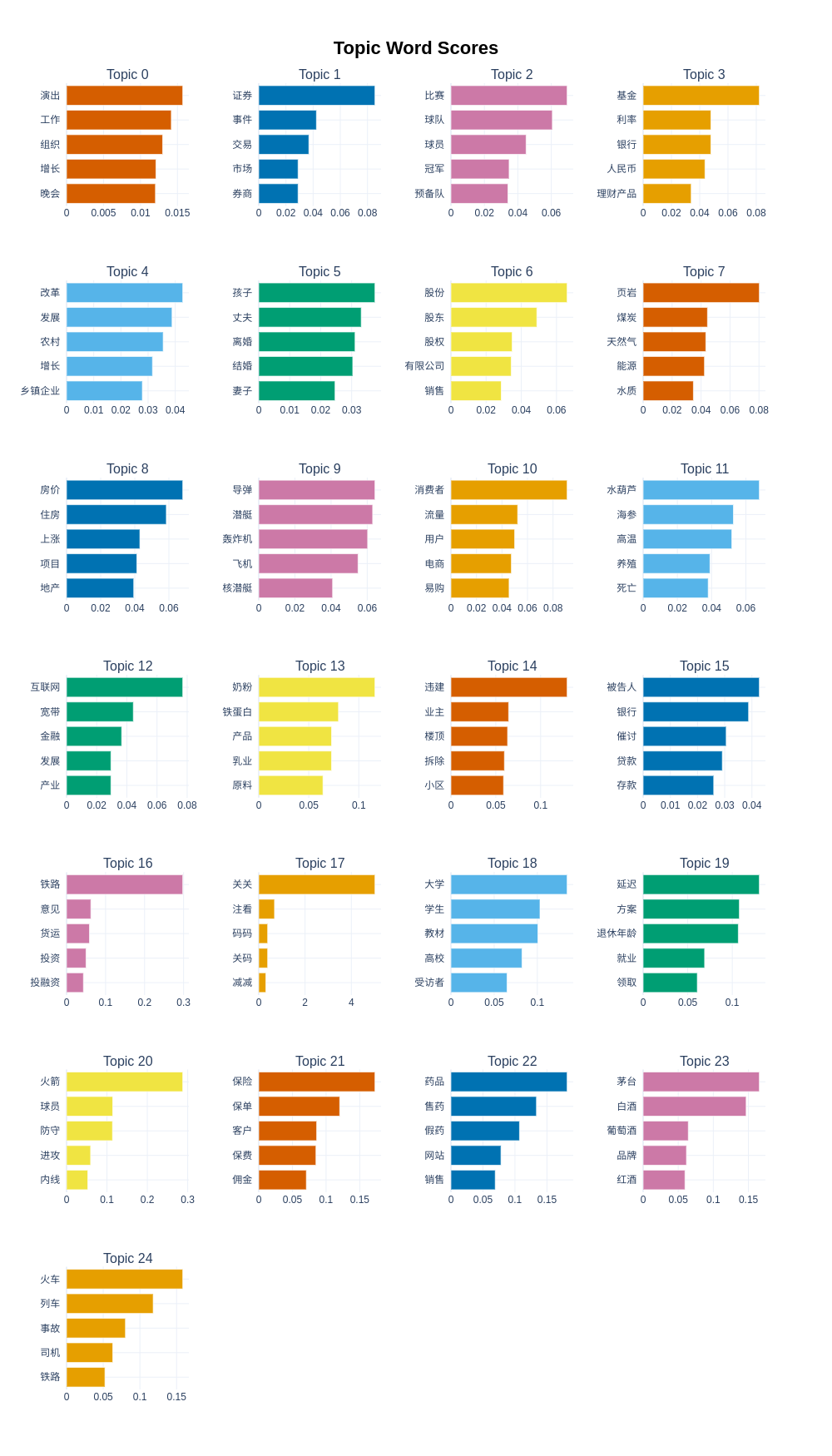
1、展示每个topic里权重最高的前五个词

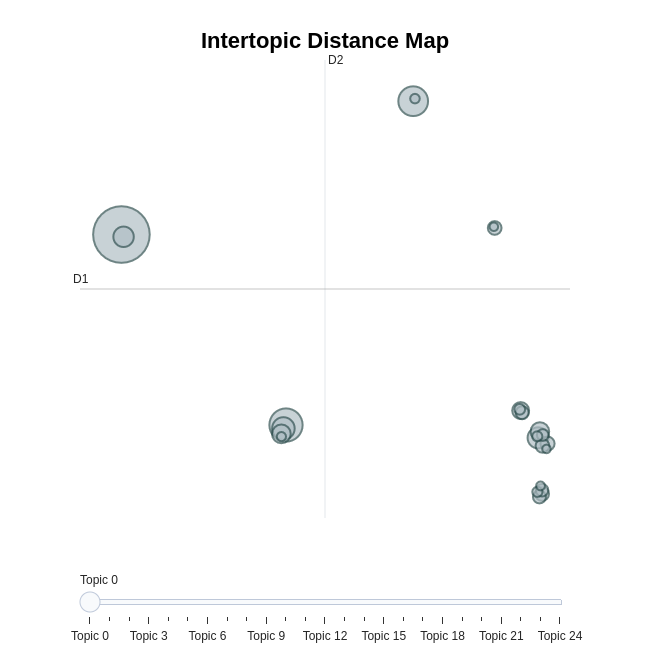
2、可视化展示topic的类簇分布

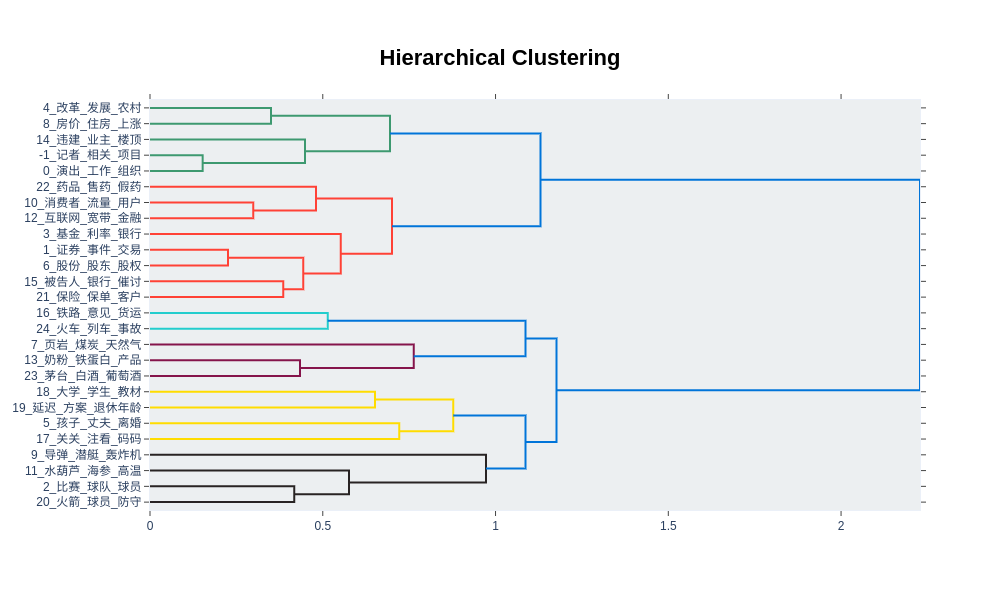
3、可视化层次结构

Topic的生成结果还是很赞的。

总结

BERTopic的组件化结构设计非常好，不管是用于文档嵌入的Transformers、降维的UMAP、聚类的HDBSCAN还是主题标题提取的c-TF-IDF，每个组件都可以用这个领域的STOA算法，未来升级也很方便，深入了解它的各个组件，也会帮助你在应用时更有感觉。