非线性最小二乘(Nonlinear Least Squares)

本文对非线性最小二乘的原理、思路和应用做了简单介绍。

非线性最小二乘

最小二乘是一种数学最优化建模方法，它的一种常见解释是对残差做了满足正态分布的极大似然估计。最小二乘分两类：线性最小二乘和非线性最小二乘，区别是残差函数是否为线性函数，线性最小二乘比较简单，可以直接求解析解，非线性最小二乘比较复杂，需要用迭代式的最优化方法求解。

最小二乘回顾

假设有观测数据集\(\{x_i,y_i\}_{i=1}^n\)，某个参数为\(w\)的函数\(f(x;w)\)描述了观测数据的因变量和自变量的映射关系，即： \[ \hat{y}_i=f(x_i;w) \] 但数据拟合时一定不是严丝合缝的，会有误差即残差，所以有： \[ y_i=\hat{y}_i+\epsilon \] 假设这个残差服从偏差为0的正态分布，则有： \[ \epsilon \sim N(0,\sigma^2) \] 于是有： \[ p(y_i|x_i,w)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{-(y_i-f(x_i;w))^2}{2\sigma^2}} \]

对于这\(n\)个独立的观测样本就会产生\(n\)个方程，采用极大似然估计有： \[ p(y|x,w)=\prod_{i=1}^n\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{-(y_i-f(x_i;w))^2}{2\sigma^2}}=\frac{1}{(\sqrt{2\pi}\sigma)^n}e^{-\sum\limits_{i=1}^n\frac{-(y_i-f(x_i;w))^2}{2\sigma^2}} \]

由贝叶斯公式可知： \[ \begin{align*} p(w|x,y)=&\frac{p(y|x,w)p(w|x)}{p(y|x)}\\ =&\frac{p(w|x)}{p(y|x)}p(y|x,w)\\ \propto&p(y|x,w) \end{align*} \] 所以，利用极大似然求参有： \[ \begin{align*} arg\max\limits_w p(w|x,y)&=arg\min\limits_w -ln(p(y|x,w))\\ &=n\ln\sqrt\sigma+\sum\limits_{i=1}^n\frac{(y_i-f(x_i;w))^2}{2\sigma^2}\\ &\propto\frac{1}{2\sigma^2}\sum\limits_{i=1}^n (y_i-f(x_i;w))^2 \end{align*} \] 最后有： \[ w=arg\min\limits_w \sum\limits_{i=1}^n (y_i-f(x_i;w))^2 \]

非线性最小二乘

当残差函数非线性时，方便起见，我们定义残差函数为：\(r(w)=y-f(x;w)\)，对\(n\)个观测样本有\(n\)个方程： \[ F(w)=[r_1(w),r_2(w),......,r_n(w)]^T \] 非线性最小二乘问题变成： \[ \min ||r(w)||^2=r_1(w)^2+r_2(w)^2+......r_n(w)^2 \] 如果此时还有其他约束条件，例如，等式约束\(q(w)=0\)的话，以上问题变成了约束非线性最小二乘问题： \[ \begin{align*} \min &\quad ||r(w)||^2=r_1(w)^2+r_2(w)^2+......r_n(w)^2\\ s.t.& \quad q_1(w)=0\\ &\quad ......\\ &\quad q_m(w)=0 \end{align*} \]

拉格朗日乘数法

考虑求解通用的约束最优化问题，以最小化问题为： \[ \begin{align*} \min &\quad f(x)\\ s.t.& \quad q_1(x)=0\\ &\quad ......\\ &\quad q_m(x)=0 \end{align*} \] 几个定义：

1、\(x\)为\(n\)维向量，当\(x\)满足以上所有约束条件时，被叫做可行解；

2、所有可行解中，当满足\(f(x^*)\leq f(x)\)，则\(x^*\)被称作全局最优解；

3、当可行解只有在一个邻域\(R\)中时才满足\(f(x^*)\leq f(x)\)，则\(x^*\)被称作局部最优解，其中\(||x-x^*||\leq R\)。

为求解上述约束问题，需要将其转变为无约束问题，在机器学习与人工智能技术分享-第四章 最优化原理中有过介绍，定义拉格朗日函数： \[ \begin{align*} L(x,\lambda)&=f(x)+\lambda_1 q_1(x)+\lambda_2 q_2(x)+...+\lambda_m q_m(x)\\ &=f(x)+\lambda^T q(x) \end{align*} \] 其中：\(\lambda=(\lambda_1,\lambda_2,...,\lambda_m)\)为\(m\)维的拉格朗日乘子向量，\(q(x)=(q_1(x),q_2(x),...,q_m(x))\)为\(m\)维的约束函数向量。

拉格朗日函数的梯度为： \[ \nabla L(x,\lambda)= \begin{bmatrix} \nabla_x L(x,\lambda)\\ \nabla_\lambda L(x,\lambda) \end{bmatrix} \] 其中： \[ \begin{align*} \nabla_x L(x,\lambda)&=\nabla f(x)+\lambda_1 \nabla q_1(x)+...+\lambda_m \nabla q_m(x)\\ &=\nabla f(x)+D q(x)^T\lambda\\ \nabla_\lambda L(x,\lambda)&=q(x) \end{align*} \]

如果可行解\(x^*\)为局部最优解，则必须满足拉格朗日条件(first-order necessary conditions)，即此条件是必要条件： \[ \begin{align*} \nabla f(x^*)+D q(x^*)^T\lambda^*&=0\\ q(x^*)&=0 \end{align*} \]

其中： \[ 𝐷q(𝑥)= \begin{gathered} \begin{bmatrix} \frac{\partial q_1(x)}{\partial x_1} & \cdots & \frac{\partial q_1(x)}{\partial x_n} \\ \vdots & & \vdots\\ \frac{\partial q_m(x)}{\partial x_1} & \cdots & \frac{\partial q_m(x)}{\partial x_n} \\ \end{bmatrix}= \begin{bmatrix} \nabla q_1(x)^T \\ \vdots\\ \nabla q_m(x)^T \\ \end{bmatrix} \end{gathered} \]

需要注意，如果在可行解\(x\)下，\(𝐷q(𝑥)=\{\nabla q_1(x),...,\nabla g_m(x)\}\)是线性相关的，则拉格朗日乘子不存在，因此无法通过拉格朗日乘数法求解，但此时局部最优解可能是存在的； 反之，如果\(𝐷q(𝑥)\)线性无关，则\(x\)被称为正则点（regular point），举个例子： \[ \begin{align*} \min &\quad f(x_1,x_2)=x_1+x_2\\ s.t.& \quad q_1(x_1,x_2)=(x_1-1)^2+x_2^2-1=0\\ &\quad q_2(x_1,x_2)=(x_1-2)^2+x_2^2-4=0 \end{align*} \]

\(x^*=(0,0)\)为唯一的可行解，因此它也是最优解，其拉格朗日函数为： \[ L(x,\lambda)=x_1+x_2+\lambda_1((x_1-1)^2+x_2^2-1)+\lambda_2((x_1-2)^2+x_2^2-4) \] 在\(x^*=(0,0)\)处的拉格朗日条件为： \[ \begin{align*} \nabla_x L(x,\lambda)&=\begin{bmatrix}1\\1\end{bmatrix}+2\lambda_1\begin{bmatrix}x_1-1\\x_2\end{bmatrix}+2\lambda_2\begin{bmatrix}x_1-2\\x_2\end{bmatrix}=0\\ \nabla_\lambda L(x,\lambda)&=\begin{bmatrix}(x_1-1)^2+x_2^2-1=0\\(x_1-2)^2+x_2^2-4=0\end{bmatrix} \end{align*} \] 显然，\(\lambda_1\)和\(\lambda_2\)都不存在，\(x^*=(0,0)\)不是正则点(\(\nabla q_1(x)\)与\(\nabla q_2(x)\)是线性相关的)，无法使用拉格朗日乘数法求解该问题。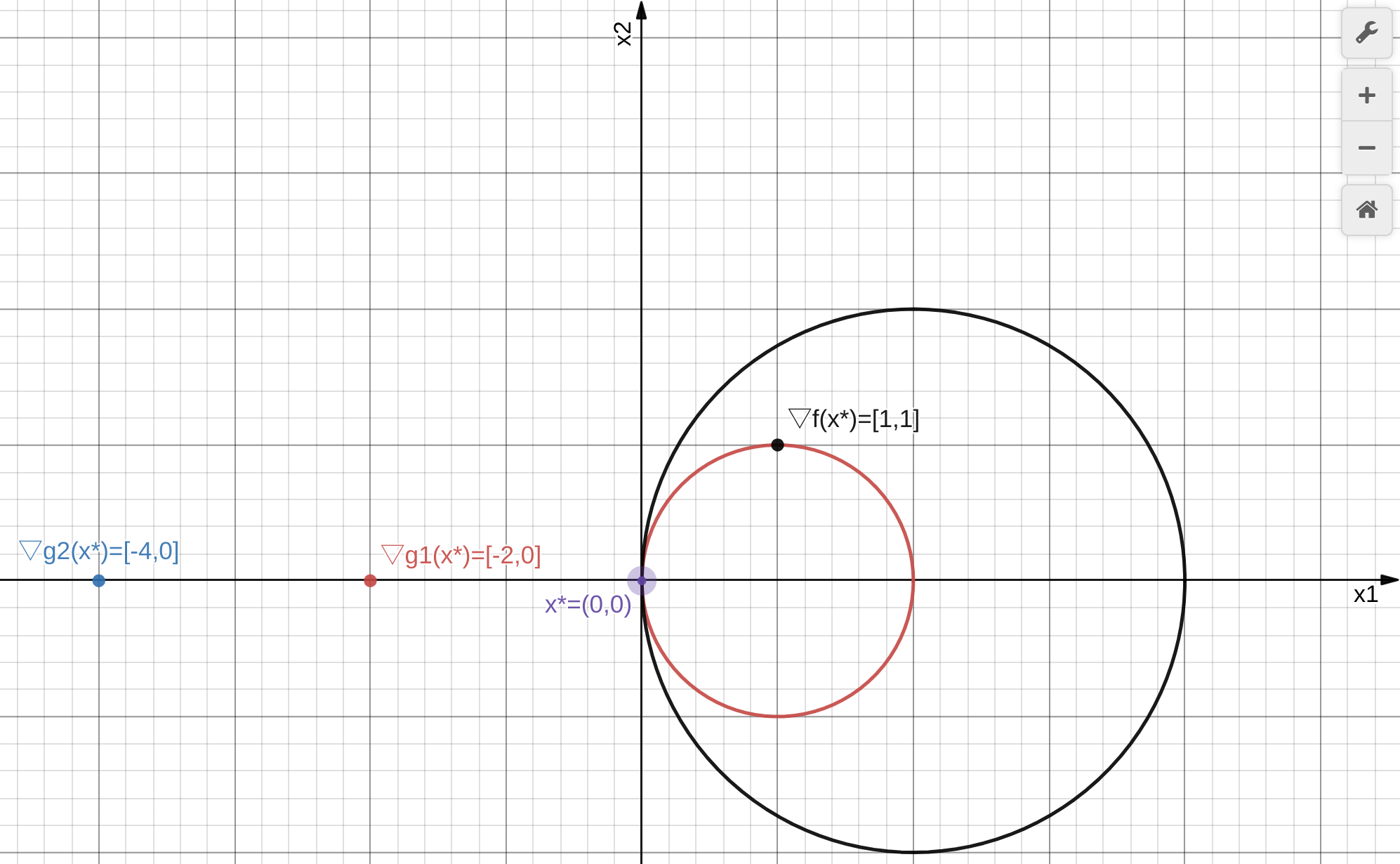

约束非线性最小二乘

\[ \begin{align*} \min &\quad ||r(w)||^2\\ s.t.& \quad q(w)=0\\ \end{align*} \]

其中\(w\)为待求参数，\(r(w)=(r_1(w),...,r_n(w))\)为\(n\)个样本的残差，\(q(w)=(q_1(w),...,q_m(w))\)为\(m\)个约束条件。

转化为拉格朗日函数：\(L(w,\lambda)=||r(w)||^2+\lambda^Tq(w)\)，由拉格朗日条件知，如果\(w^*\)为最优解，则存在\(\lambda^*\)使得： \[ 2Dr(w^*)^Tr(w^*)+Dq(w^*)^T\lambda^*=0,\quad q(w^*)=0 \]

ps:\(Dq(w^*)\)的行向量为线性无关组。

当\(r(w)\)和\(q(w)\)都是线性函数时，该问题可以直接求出解析解，否则需要采用迭代法，在机器学习与人工智能技术分享-第四章 最优化原理中我们介绍了由泰勒展开式衍生出的各种一阶和二阶优化算法，例如各种梯度下降法和各种拟牛顿法， 简单地说，优化算法就是在研究怎么找方向和找步长，先找方向再找步长是Line Search方法，先找步长再找方向（也可以看做同时找步长和方向）是Trust Region方法。

Newton Step-based迭代法

前面也说到泰勒展开式是大部分最优化方法的“根”，如果展开到二阶，则可以变成各种牛顿法，简单回顾： 求解无约束最小化问题： \[ \min f(x) \] 在当前迭代\(x_k\)点下，做泰勒展开到二阶： \[ f(x_k+\Delta x_k)=f(x_k)+\nabla f(x_k)^T \Delta x_k+\frac{1}{2}\Delta x_k^T\nabla^2 f(x_k+t\Delta x_k)\Delta x_k \] 其中：\(t=(0,1)\)是个缩放因子，迭代式为：\(x_{k+1}=x_k+\Delta x_k\)。

简单起间用\(f_k\)代替\(f(x_k)\)，用\(g_k\)代替\(\nabla f(x_k)\)，用\(p_k\)代替\(\Delta x_k\)有： \[ f(x_k+p_k)=f_k+g_k^T p_k+\frac{1}{2}p_k^T\nabla^2 f(x_k+tp_k)p_k \] 由于Hessian矩阵\(H_k=\nabla^2 f(x_k)\)计算成本很高，所以用一个矩阵\(B_k\)去估计\(H_k\)，于是上面问题变成： \[ m_k(p_k) = f_k + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \] 其中：\(m_k (p_k)\)与\(f(x_k+p_k)\)之间的误差是\(||p_k||^2\)的高阶无穷小，即：\(O(||p_k||^2)\)，当\(p_k\)很小时这个误差就很小。 由最优值必要条件可知，在第\(k\)轮迭代有： \[ \begin{align*} \nabla m_k(p_k)&=g_k+B_kp_k=0\\ &\Leftrightarrow B_k p_k = −g_k \end{align*} \]

1、如果\(B_k=H_k\)且\(H_k\)可逆、正定，上面问题就变成了牛顿法；

2、如果\(B_k\approx H_k\)且\(B_k\)始终保持正定，就是拟牛顿法，它和牛顿法一样，都具有二次收敛速度，即： 当\(x_k\)靠近最优值\(x^*\)时，有：\(||x_{k+1}-x^*||<\epsilon||x_k-x^*||^2\)，\(\epsilon<1\)；

ps：只有\(B_k\)始终保持正定才能保证收敛，因为，对于最小化问题，始终希望搜索方向是一个下降方向，即满足\(p_k^Tg_k<0\)，所以： \[ \begin{align*} p_k^Tg_k&<0\\ B_k p_k &= −g_k\\ &\Leftrightarrow p_k^TB_k p_k >0 \end{align*} \]

3、如果\(B_k=I\)，显然单位矩阵不是Hessian矩阵的一个好的估计，但它够简单，于是有：\(p_k=-g_k\)，这就是妥妥的梯度下降法了，这时的收敛速度只能到线性速度了，即：\(||x_{k+1}-x^*||<\epsilon||x_k-x^*||\)，\(\epsilon<1\)；

4、如果\(H_k\)非正定，需要重新定义\(B_k=H_k+\lambda I\)，总能找到\(\lambda\)使得\(B_k\)正定，即\(B_k p_k = −g_k \Leftrightarrow (H_k+\lambda I)p_k = −g_k\)，从而总能找到最优\(p_k\)，换个角度看这个形式：

• 当\(\lambda\)很小时，如果\(H_k\)正定，上式蜕变为牛顿法；
• 当\(\lambda\)很大时，出现两个现象： 1、上式蜕变为梯度下降法 2、\(||p_k||\)会被减小

这个优化框架其实就是原始的Levenberg-Marquardt迭代法，即：当前值在距离最优值比较远时通过梯度下降法优化，虽然速度很慢但保证收敛，接近最优值时通过牛顿法以二次收敛速度逼近。 实际上可以证明，即使\(B_k\)不正定，只要对\(||p_k||\)做合适的限制，就能做到全局收敛，这个思想就是Trust Region（信任域）法。 回看这个问题： \[ \min m_k(p_k) = f_k + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \] 当\(B_k=H_k\)时，相当于泰勒展开式展开到3阶，此时误差为\(O(||p_k||^3)\)，当\(||p_k||\)很小时，这个误差非常非常小，所以确定\(||p_k||\)这一步可以转化为一个子优化问题： \[ \begin{align*} \min &\quad m_k(p_k) = f_k + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \\ s.t.&\quad ||p_k||\leq\Delta_k \end{align*} \] 其中\(\Delta_k>0\)，是Trust Region的半径，定义\(||.||\)为欧氏距离，则最优解\(p*\)在一个半径为\(\Delta_k\)的球体内（把约束变个形式就清楚了：\(||p_{k}|| \leq \Delta_{k} \Leftrightarrow p_{k}^{T}p_{k} \leq \Delta_{k}^{2}\)），特别是当Hessian矩阵性质不太好（如出现奇异或者病态）时，Trust Region法却能很好的求解。

ps：由于目标函数和约束条件都是二次方形式，所以求解的计算成本比较低。

总结对比下Levenberg-Marquardt与Trust Region的区别：

当牛顿法不好使时：

Levenberg-Marquardt：通过对\(H_k\)做扰动，求解\((H_k+\lambda I)p_k = −g_k\)中的\(p_k\)，从而做迭代；

Trust Region：通过求解子优化问题\(\min m_k(p_k) = f_k + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \quad s.t. ||p_k||\leq\Delta_k\)得到最优\(p_k\)，从而做迭代，让当前点\(x_k\)迅速进入”兴趣域“。

所以Trust Region法可以看做是Levenberg-Marquardt法演化后得到的算法，另外，前者可以很好的处理目标函数是Negative Curvature的情况，后者不行，所以不要将两类算法混为一谈。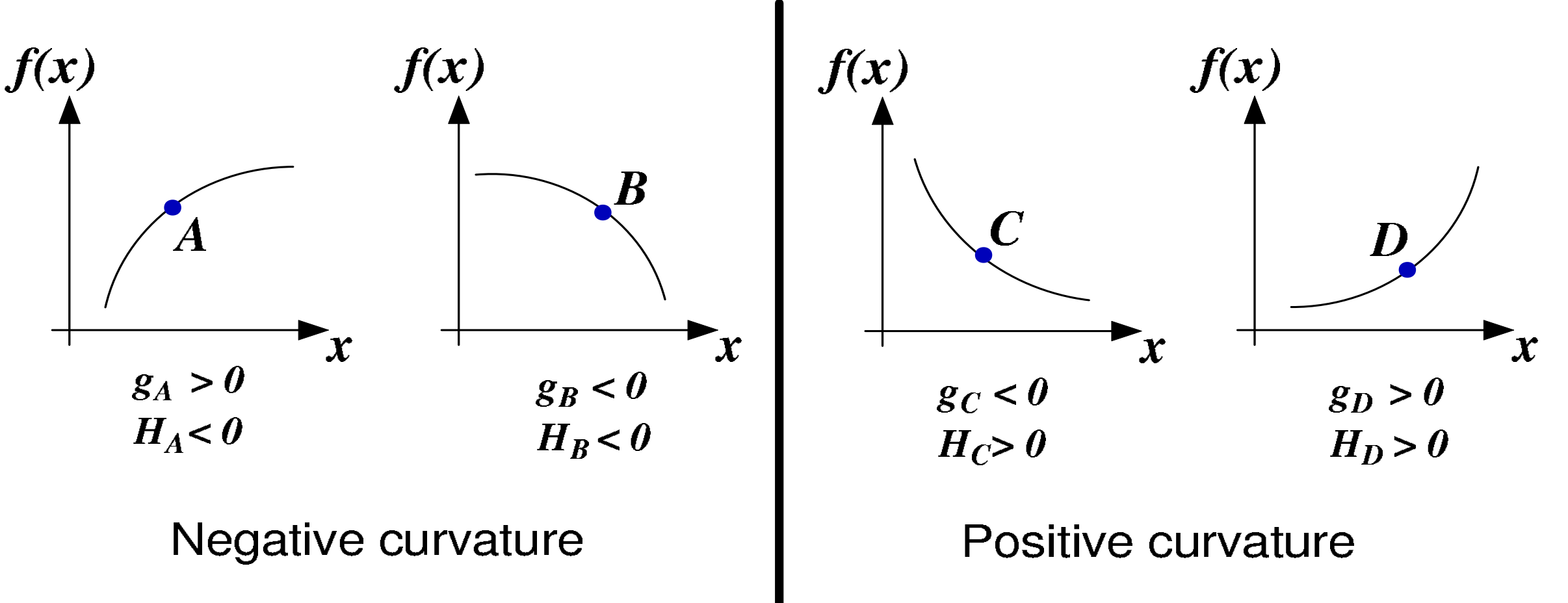

到此为止，Trust Region还有个遗留问题是\(\Delta_k\)该怎么取？ 给定\(p_k\)，定义： \[ \rho_k = \frac{f(x_k)-f(x_k+p_k)}{m_k(0)-m_k(p_k)} \]

观察上述定义：

1、当\(\rho_k<0\)时，由于\(f(x_k+p_k)\)大于当前值，所以目标函数值上升了，此时的\(p_k\)必须丢弃；

2、如果\(\rho_k\)接近1，说明\(m_k\)估计的比较好，此时就可以放心的再下次迭代时扩展信任域；

3、如果\(\rho_k>0\)且远小于1，则下次迭代保持信任域不变；

4、如果\(\rho_k\)接近0，则需要在下次迭代时缩减信任域。

Trust Region伪码如下：

\[ \begin{align*} &\textbf{Trust Region Algorithm}\\ &\quad \text{给定上界}\hat{\Delta}>0,\Delta_0 \in(0, \hat{\Delta}), \eta \in [0, \frac{1}{4})\\ &\quad \textbf{for } k \text{ in range(0,..)}\\ &\quad \qquad \text{求解}\min m_k(p_k) = f_k + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \quad s.t. ||p_k||\leq\Delta_k\\ &\quad \qquad \text{得到最佳}p_k\\ &\quad \qquad \text{计算}\rho_k\\ &\quad \qquad \textbf{if }\rho_k<\frac{1}{4}\\ &\quad \qquad \qquad \quad \Delta_{k+1}=\frac{1}{4}\Delta_k\\ &\quad \qquad \textbf{else }\\ &\quad \qquad \qquad \quad \textbf{if }\rho_k>\frac{3}{4}\text{ 且 }||p_k||=\Delta_k\\ &\quad \qquad \qquad \quad \qquad \Delta_{k+1}=\min(2\Delta_k,\hat{\Delta})\\ &\quad \qquad \qquad \quad \textbf{else }\\ &\quad \qquad \qquad \quad \qquad \Delta_{k+1}=\Delta_k\\ &\quad \qquad \textbf{if } \rho_k>\eta\\ &\quad \qquad \qquad \quad x_{k+1}=x_k+p_k\\ &\quad \qquad \textbf{else }\\ &\quad \qquad \qquad \quad x_{k+1}=x_k\\ &\quad \textbf{end } \end{align*} \]

Trust Region框架应用

1、问题变换

回到之前的问题，为方便后续推理，去掉等式约束（因为通过拉格朗日乘数法可以很容易变成无约束问题），加入迭代轮数标识\(k\)，并给目标函数加个系数，即： \[ \begin{align*} \min &\quad \frac{1}{2}||r(w_k)||^2\\ \end{align*} \] 由泰勒展开式可知： \[ r(w_k+p_k)=\frac{1}{2}||r(w_k+p_k)||^2\approx\frac{1}{2}||Dr(w_k)p_k+r(w_k)||^2 \]

方便起见用符号\(J_k\)表示Jacobian矩阵\(Dr(w_k)\)，\(r_k\)表示\(r(w_k)\)，\(q_k\)表示\(q(w_k)\)： \[ r(w_k+p_k)\approx\frac{1}{2}||J_{k} p_k+r_k||^2 \]

即待求解的无约束问题从 \[ \begin{align*} \min &\quad \frac{1}{2}||r(w_k)||^2\\ \end{align*} \] 变成： \[ \min \frac{1}{2}||J_{k} p_k+r_k||^2 \]

利用Trust Region 框架，如果\(p_k^*\)为上述问题的最优解，则一定存在\(\lambda^* \geq 0\)，且满足以下条件： \[ \begin{align*} (J_k^{T}J_k+\lambda^*I)p_k^*&=-J_k^{T}r_k\\ \lambda^*(\Delta_k-||p_k^*||)&=0 \end{align*} \]

换个角度看，\((J^{T}J+\lambda^*I)p_k^*=-J^{T}r_k\)其实就是求解下面这个最小二乘问题： \[ \min_p\frac{1}{2}||\left [ \begin{matrix} J_k \\ \sqrt{\lambda}I \end{matrix} \right ]p+\left [ \begin{matrix} r_k \\ 0 \end{matrix} \right ]||^2 \]

2、Trust Region框架下描述解法

\[ \begin{align*} &\quad \text{给定上界}\hat{\Delta}>0,\Delta_0 \in(0, \hat{\Delta}), \eta \in [0, \frac{1}{4})\\ &\quad \textbf{for } k \text{ in range(0,..)}\\ &\quad \qquad \text{求解}\min m_k(p_k) = \frac{1}{2}||J_{k} p_k+r_k||^2 + g_k^T p_k + \frac{1}{2} p_k^T B_k p_k \quad s.t. ||p_k||\leq\Delta_k\\ &\quad \qquad \text{1、当$p_k$满足约束条件}||p_k||<\Delta_k:\\ &\quad \qquad \qquad \text{则采用Gauss–Newton法有:}\nabla m_k(p_k)=0 \Rightarrow J_k^TJ_kp_k=-J_k^Tr_k\\ &\quad \qquad \qquad \text{这种方法有几个好处：}\\ &\quad \qquad \qquad \text{a.不像Newton法需要计算Hessian矩阵，从而大大提高计算效率}\\ &\quad \qquad \qquad \text{b.用$J^TJ$估计Hessian矩阵使得其收敛速度接近Newton法}\\ &\quad \qquad \qquad \text{c.只要$J_k$满秩且目标函数梯度不为0，$p_k$一定是目标函数的下降方向}\\ &\quad \qquad \qquad \text{d.可以利用线性最小二乘法寻找搜索方向}\\ &\quad \qquad \text{2、当$p_k$满足约束条件}||p_k||=\Delta_k:\\ &\quad \qquad \qquad \text{则有:}\\ &\quad \qquad \qquad (J_k^{T}J_k+\lambda^*I)p_k^*=-J_k^{T}r_k\\ &\quad \qquad \qquad\lambda^*(\Delta_k-||p_k^*||)=0\\ &\quad \qquad \qquad\lambda^* \geq 0\\ &\quad \qquad \text{得到最佳}p_k\\ &\quad \qquad \text{计算}\rho_k\\ &\quad \qquad \textbf{if }\rho_k<\frac{1}{4}\\ &\quad \qquad \qquad \quad \Delta_{k+1}=\frac{1}{4}\Delta_k\\ &\quad \qquad \textbf{else }\\ &\quad \qquad \qquad \quad \textbf{if }\rho_k>\frac{3}{4}\text{ 且 }||p_k||=\Delta_k\\ &\quad \qquad \qquad \quad \qquad \Delta_{k+1}=\min(2\Delta_k,\hat{\Delta})\\ &\quad \qquad \qquad \quad \textbf{else }\\ &\quad \qquad \qquad \quad \qquad \Delta_{k+1}=\Delta_k\\ &\quad \qquad \textbf{if } \rho_k>\eta\\ &\quad \qquad \qquad \quad x_{k+1}=x_k+p_k\\ &\quad \qquad \textbf{else }\\ &\quad \qquad \qquad \quad x_{k+1}=x_k\\ &\quad \textbf{end } \end{align*} \]

罚函数法

对问题： \[ \begin{align*} \min &\quad ||r(w)||^2\\ s.t.& \quad q(w)=0\\ \end{align*} \] 不再强制要求约束条件严格遵守：\(q(w)=0\)，而是增惩罚系数，变成无约束问题： \[ \min ||r(w)||^2+\mu||q(w)||^2,\mu>0. \] 在每轮迭代\(k\)中，通过求解： \[ \min ||r(w)||^2+\mu_k||q(w)||^2,\mu_k>0. \] 利用Levenberg–Marquardt算法更新\(w_{k+1}\)，方便起见用符号\(J_k\)表示Jacobian矩阵\(Dr(w_k)\)，\(r_k\)表示\(r(w_k)\)，\(q_k\)表示\(q(w_k)\)，根据拉格朗日条件有： \[ 2J_kr_k+2\mu_{k-1}Dq_k^Tq_k=0 \] 令\(z_{k}=2\mu_{k-1}q_k\)，则有： \[ 2J_kr_k+Dq_k^Tz_{k}=0 \] 当\(||q_k||\)足够小时算法结束迭代（此时\(\mu_{k-1}\)足够大）。

算法缺点：

为了让\(q_k\)尽快逼近到0，需要惩罚系数\(\mu\)的值快速增大，这个会带来：

1、求解非线性最小二乘子问题变得困难

2、会导致Levenberg–Marquardt算法需要更多的迭代甚至失败

增广拉格朗日法

对问题： \[ \begin{align*} \min &\quad ||r(w)||^2\\ s.t.& \quad q(w)=0\\ \end{align*} \] 其最优值满足拉格朗日条件： \[ 2Dr(w^*)r({w^*})+Dq(w^*)^T \lambda^*=0,\quad q(w^*)=0 \] 定义增广拉格朗日函数： \[ \begin{align*} L_{\mu}(w,\lambda)&=L(w,\lambda)+\mu||q(w)||^2\\ &=||r(w)||^2+q(w)^T\lambda+\mu||q(w)||^2\\ &=||r(w)||^2+\mu||q(w)+\frac{1}{2\mu}\lambda||^2-\frac{1}{4\mu}||\lambda||^2\\ \mu&>0\\ \end{align*} \] 根据拉格朗日条件知最优值\(w^*\)满足： \[ \begin{align*} &2Dr(w^*)r({w^*})+2\mu Dq(w^*)^T(q(w^*)+\frac{1}{2\mu}\lambda)=0\\ \Rightarrow&\\ &2Dr(w^*)r({w^*})+Dq(w^*)^T(2\mu q(w^*)+\lambda)=0\\ \end{align*} \] 令\(\lambda^*=\lambda + 2\mu q(w^*)\) 有： \[ 2Dr(w^*)r({w^*})+Dq(w^*)^T \lambda^*=0 \] 显然，根据拉格朗日条件可知，如果\(w^*\)是最优解，必须满足\(q(w^*)=0\)，当它的值较大时，可以通过上述\(\lambda\)的迭代式进行迭代。完整表述如下： \[ \begin{align*} &\text{1.利用LM算法在}w_k\text{点开始迭代求解问题:}\min ||r(w_k)||^2+\mu_k||q(w_k)+\frac{1}{2\mu_k}\lambda_k||^2 \text{，得到}w_{k+1}\\ &\text{2.更新迭代式:}\lambda_{k+1}=\lambda_k + 2\mu_k q(w_{k+1})\\ &\text{3.更新惩罚系数:} \mu_{k+1}= \left\{ \begin{aligned} \mu_k & = \text{if}\quad ||q(w_{k+1})||<\frac{1}{4} ||q(w_{k})||\\ 2\mu_k & = \text{otherwise} \\ \end{aligned} \right. \end{align*} \] 迭代初始点可以选择：\(\lambda_1=0,\mu_1=1\)，和罚函数法不同，\(\mu\)只在需要时增加，增长速度缓慢，当\(q(w_k)\)足够小或者达到最大迭代次数后算法结束。

汽车非线性控制问题

阿克曼转向技术

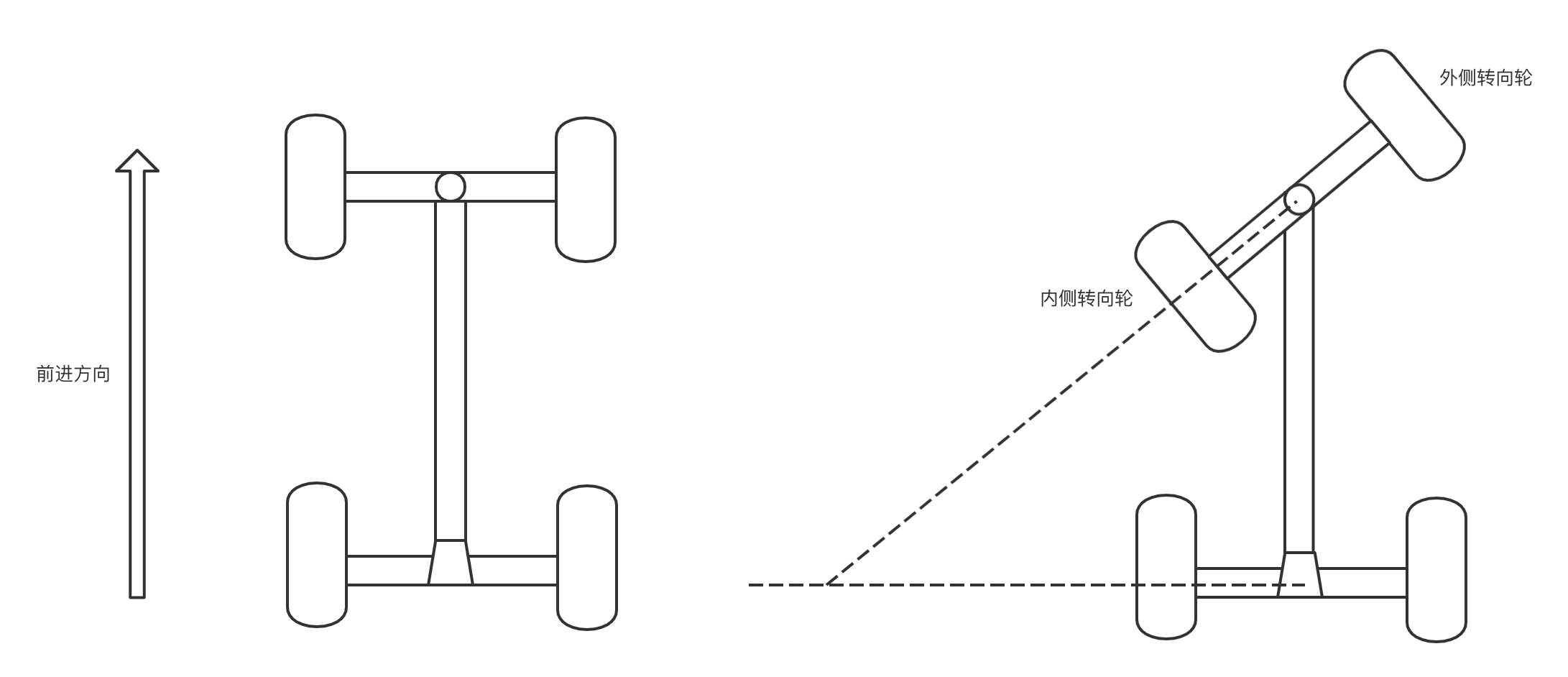
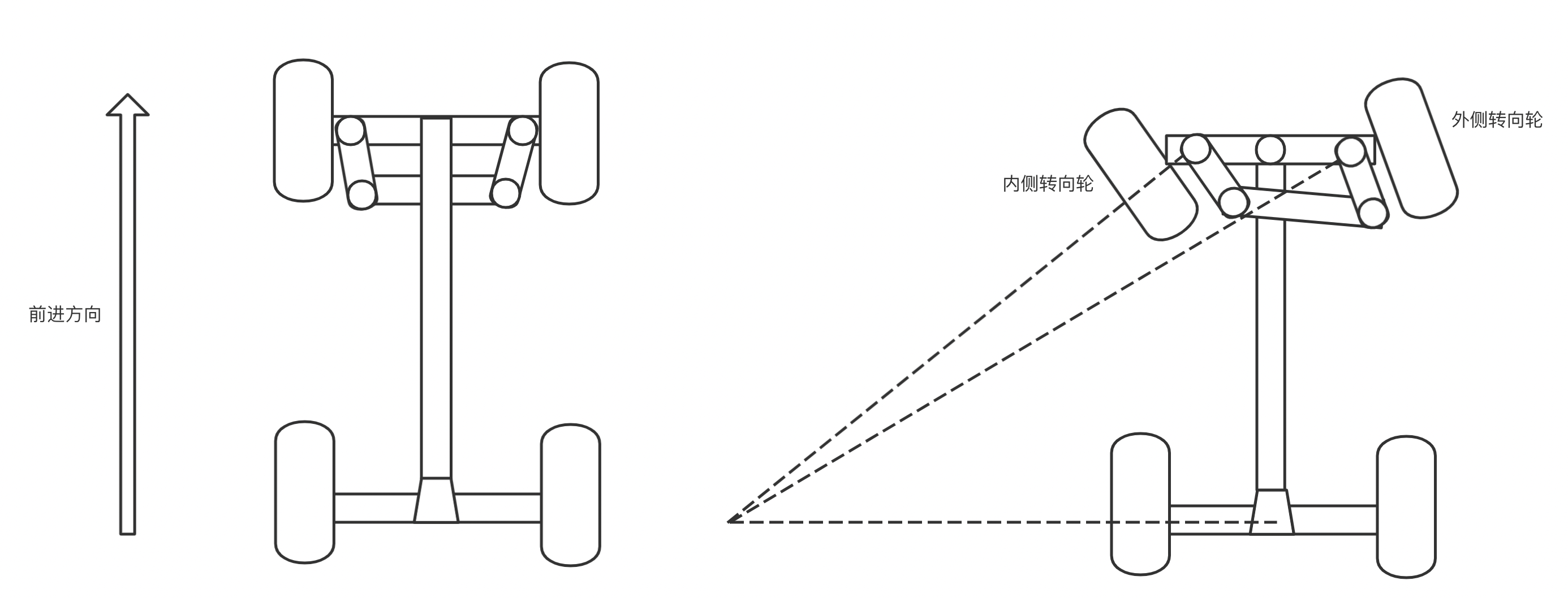
很长时间人们在车辆（如：马车）转向上采用单铰链转向技术，如下图，这种方式两个前轮的转向角是相同的，内外转向轮指向同一圆心，结构很简单，但转向摆动空间大时会影响稳定性，转弯角度大时也会发生卡死，就像小时候开玩具车时，转弯时一个不小心就人仰马翻。为了避免上述问题，人们发明了一种转向结构，让内侧转向轮的转角比外侧转向轮大了约2~4度，并让四个轮子路径的圆心大致交会于后轴的延长线上的同一个中心点，从而能够平滑稳定的转向，后来这项技术被英国代理商阿克曼申请了专利，后被称作阿克曼转向技术（Ackermann Steering）如下图：

Simple Car模型

对阿克曼转向做简化，可以构建对车辆控制的简单模型：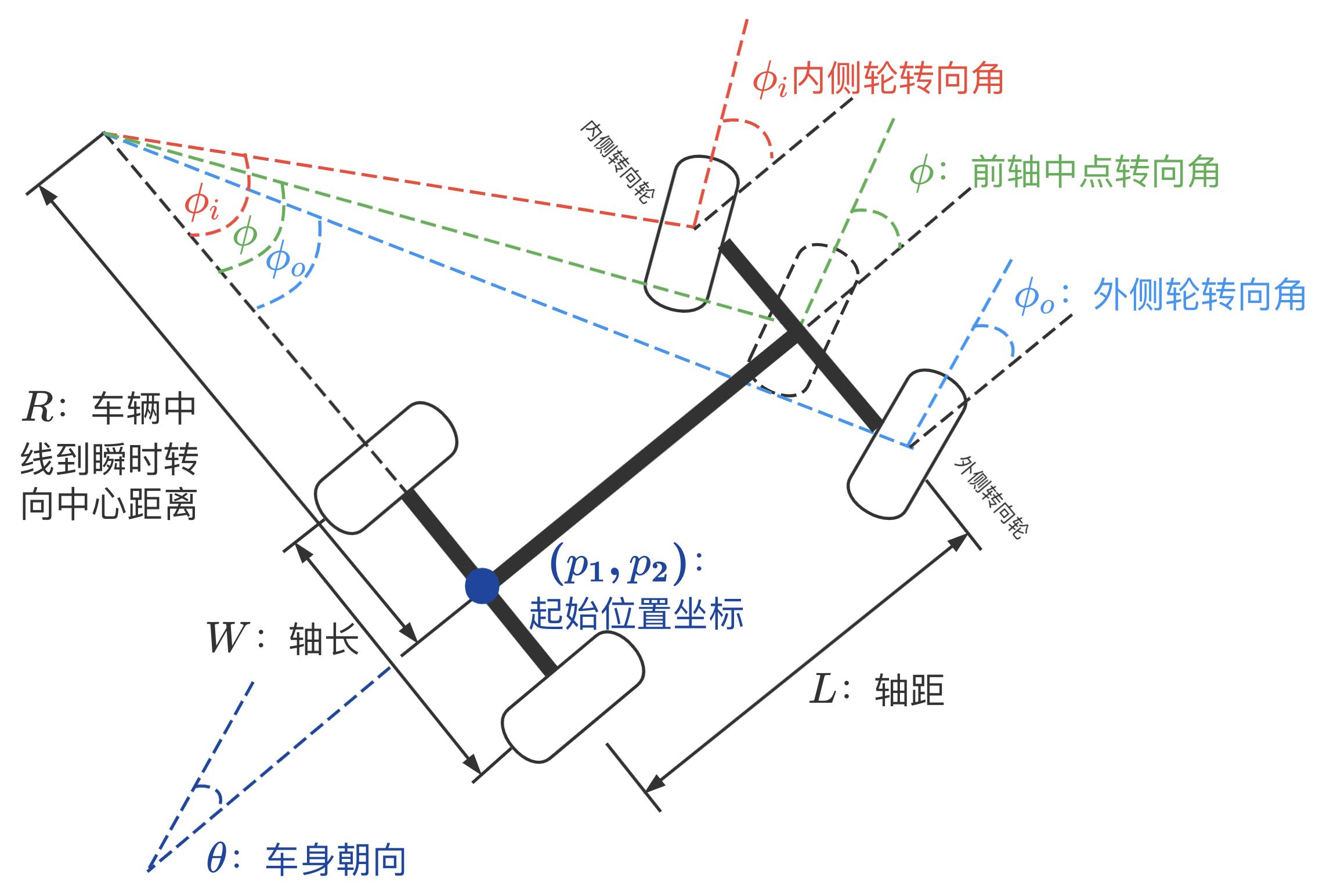

车辆在任意一个时刻\(t\)的运动模型为： \[f(p_1(t),p_2(t),v(t),\phi(t),\theta(t))\] 其中\(p_i(t),i \in \{1,2\}\)为\(t\)时刻位置，\(v(t)\)为\(t\)时刻车辆后轴中点的瞬时速度，\(\phi(t)\)为\(t\)时刻前轴中点转向角，\(\theta(t)\)为\(t\)时刻车身朝向。

内外侧轮转向角的关系为： \[ \begin{align*} &\text{内侧转向角：}\tan\phi_i=\frac{L}{R-\frac{W}{2}}\\ &\text{外侧转向角：}\tan\phi_o=\frac{L}{R+\frac{W}{2}}\\ &\text{前轴中点转向角：}\tan\phi=\frac{L}{R}\\ \end{align*} \]

\(t\)时刻后轴中点运动位置的微分方程为：

\[ \begin{align*} &\frac{dp_1}{dt}=v(t)\cos \theta(t)\\ &\frac{dp_2}{dt}=v(t)\sin \theta(t) \end{align*} \]

由弧长和角度关系可知，假设\(s\)为\(t\)时刻车辆行驶距离，则有微分方程： \[ \begin{align*} ds&=R\cdot d\theta\\ &=\frac{L}{\tan \phi}\cdot d\theta\\ \Rightarrow\\ v\cdot dt&=\frac{L}{\tan \phi}\cdot d\theta\\ \Rightarrow\\ \frac{d\theta}{dt}&=\frac{v\tan \phi}{L} \end{align*} \]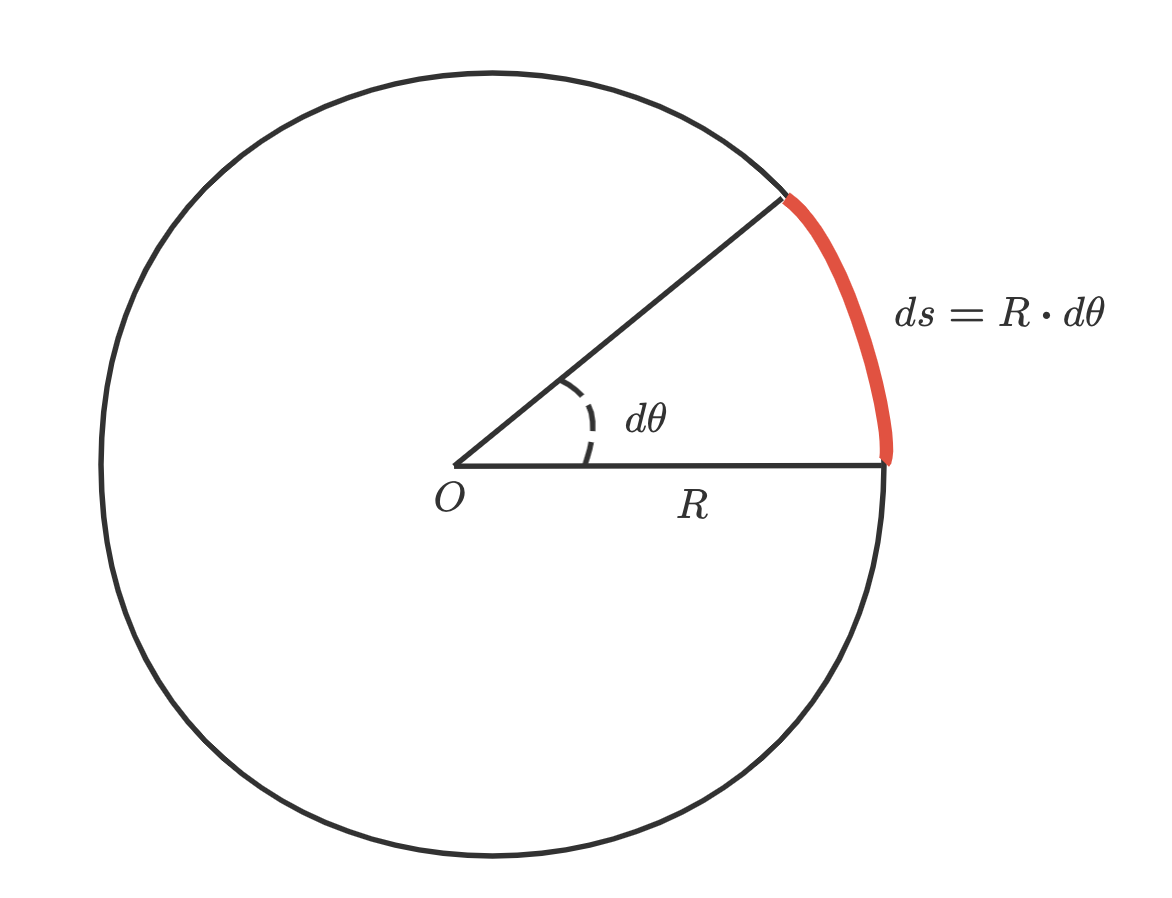

所以\(t\)时刻总的的微分方程为： \[ \begin{align*} &\frac{dp_1}{dt}=v(t)\cos \theta(t)\\ &\frac{dp_2}{dt}=v(t)\sin \theta(t)\\ &\frac{d\theta}{dt}=\frac{v(t)}{L}\tan \phi(t) \end{align*} \] 以上方程在本文叫做“车辆运动模型”。

Dubins Vehicle模型

我们思考一个问题：停车场有A、B两个位置，一个人站在A位置，在速度等约束条件同等的情况下，怎么走能最快到达B位置？答案是显而易见的，两点之间线段最短！如果把人换成车答案又是什么？由于车辆有长度和车身朝向，从一个位置到另一个位置需要依据转向角转向后才能向前行进，所以行驶的最短路径由直线段和圆弧段组成，这里最经典的方法是Dubin’s Car，这个方法最大的优点是求解最短路径规划用最简单的几何方法就能搞定，无需复杂的矩阵计算，而且Dubins在1957年完成了数学理论上的完备性证明。Dubin’s Car的控制只有三种操作：L，左转前进；R，右转前进；S，向前直行，则控制组合总共有6种： RSR、LSL、RSL、LSR、RLR、LRL，如果把L和R统一拿C（Curve）来表示的话，组合只有两种：CSC（RSR、LSL、RSL、LSR）和CCC（RLR、LRL）。

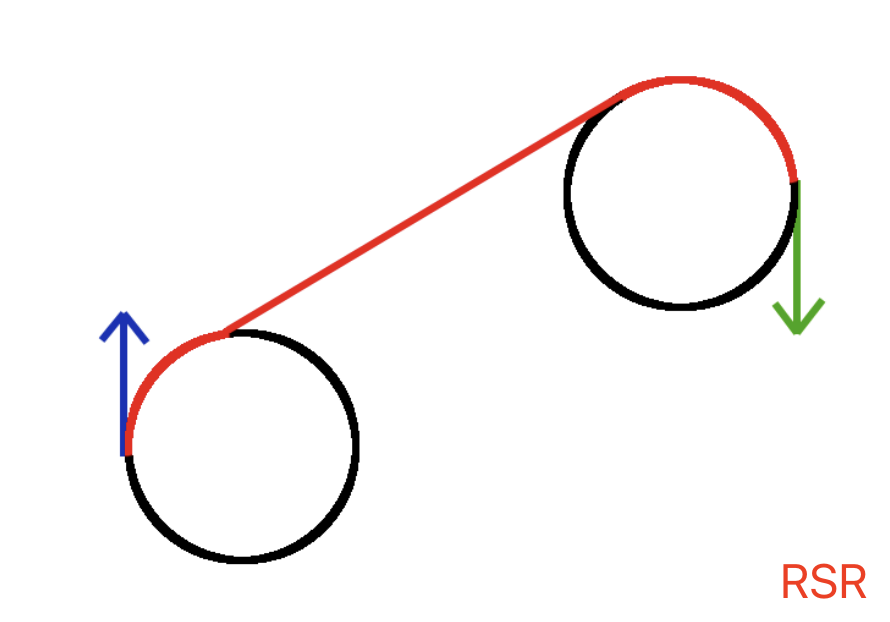
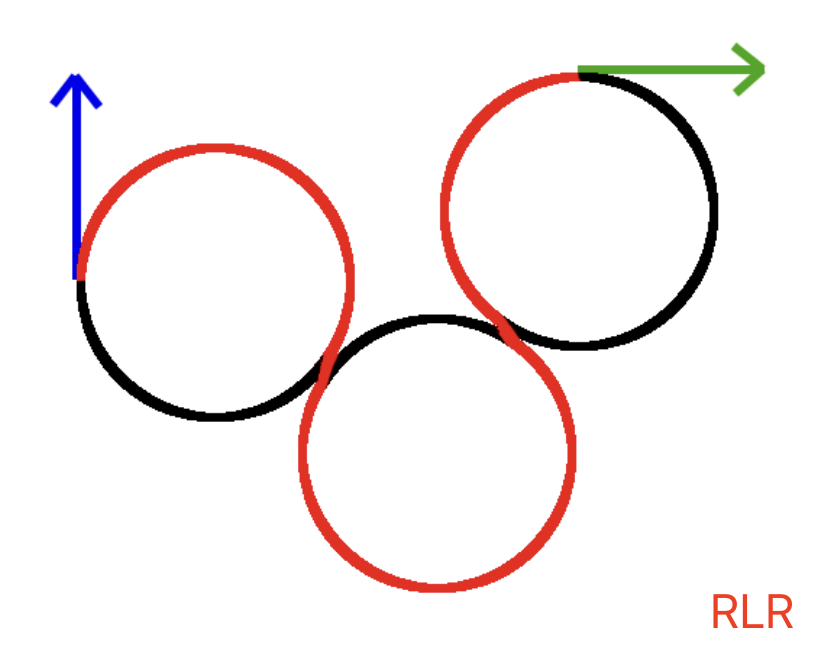
不管哪种控制方式，都有一个要遵循的独特切线。这条切线构成了“S”部分的轨迹。直线与圆相切的点是车辆必须经过的点，没有它们车辆无法完成其轨迹。所以解决这些轨迹的问题就可以归结为如何正确计算这些切线。 计算切线的方法有几何法和向量法两种，其中向量法效率更高，这里介绍下：

1、如何求两个圆的切点和切线

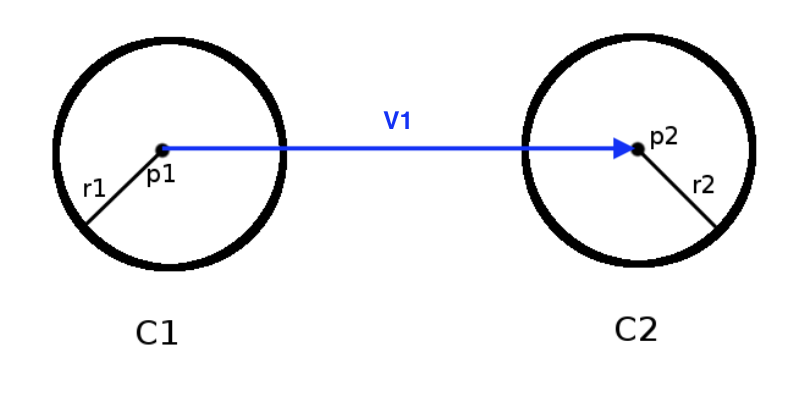
已知：两个圆\(C_1\)和\(C_2\)及其圆心位置分别为\(p_1=(x_1,y_1)\)和\(p_2=(x_2,y_2)\)，以及它们的半径\(r_1\)和\(r_2\)，它们不一定相等

求：两个圆的切点和切线

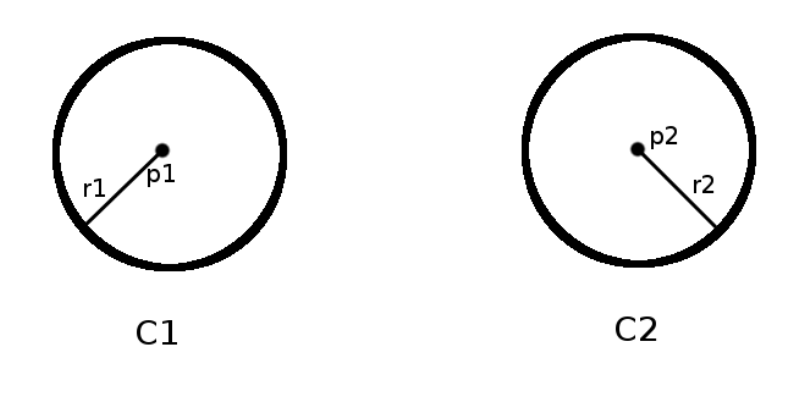
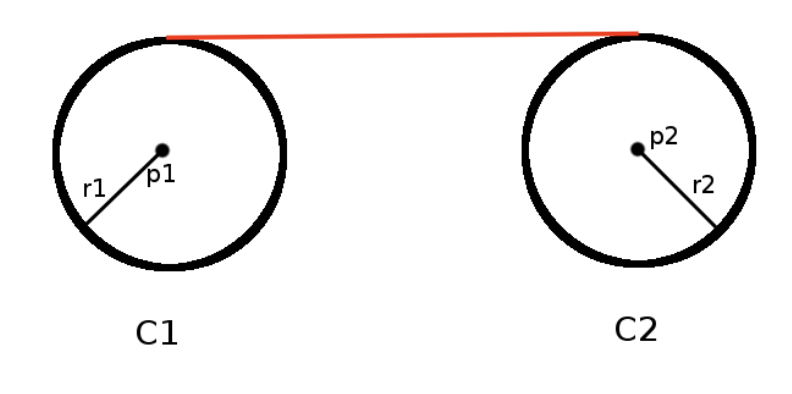
整个过程分以下几步：

• 画出两个圆\(C_1\)与\(C_2\)；
• 连接两个圆的圆心\(p_1\)和\(p_2\)，得到向量\(\vec{V_1}=(x_2-x_1, y_2-y_1)\)且\(||\vec{V_1}||=D\)
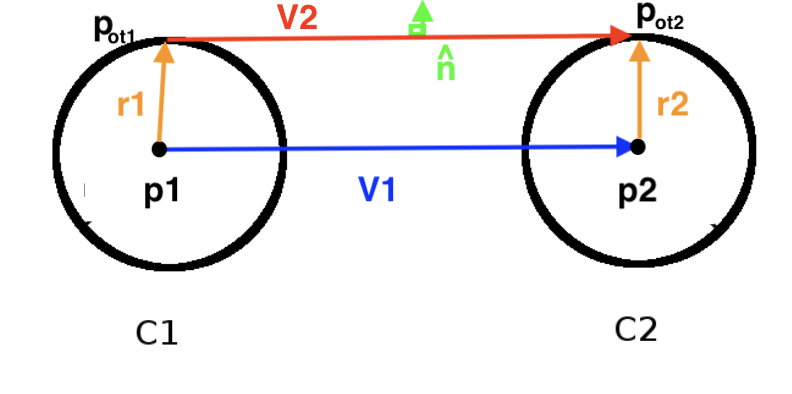
• 连接两个圆的切点\(p_{ot1}\)和\(p_{ot2}\)，得到切线\(\vec{V_2}=p_{ot2}-p_{ot1}\)
• 画出向量\(\vec{V_2}\)的单位方向向量，用\(\hat{n}\)表示
• 以上几个向量关系为：\(\vec{V_2}\cdot \hat{n}=0,\hat{n}\cdot \hat{n}=1\)
• 求切线的关键点是如何求得\(\hat{n}\)
• 修改向量\(\vec{V_1}\)为向量\(\vec{V_1}^{'}\)，使得它平行于向量\(\vec{V_2}\)：\(\vec{V_1}^{'}=\vec{V_1}-(r_2-r_1)\cdot\hat{n}\)，于是有关系： \[ \begin{align*} &\hat{n}\cdot (\vec{V_1}-(r_2-r_1)\cdot\hat{n})=0\\ &\Rightarrow \\ &\hat{n}\cdot \vec{V_1}-r_2+r_1=0\\ &\Rightarrow \\ &\hat{n}\cdot \vec{V_1}=r_2-r_1\\ &\Rightarrow \\ &\hat{n}\cdot\frac{\vec{V_1}}{D}=\frac{r_2-r_1}{D}\\ \end{align*} \] 用\(\hat{V_1}=\frac{\vec{V_1}}{D}\)，\(c=\frac{r_2-r_1}{D}\)则有： \[ \begin{align*} \hat{n}\cdot\hat{V_1}=c\\ \hat{n}\cdot \hat{n}=1\\ \hat{V_1}\cdot \hat{V_1}=1 \end{align*} \] 由点积的定义： \[ \hat{A} \cdot \hat{B} = ||A||\times||B||\cos(\theta) \] 可知，向量\(\hat{V_1}\)和\(\hat{n}\)的夹角为常量\(c\)，即： \[ \begin{align*} \cos{(\theta)}&=c\\ \sin{(\theta)}&=\sqrt{1-c^2} \end{align*} \] 这里的未知量只有：\(\hat{n}\)，问题就变成了：把已知向量\(\hat{V_1}=(v_{1x},v_{1y})\)旋转角度\(\theta\)后得到向量\(\hat{n}=(n_x, n_y)\)。 旋转向量操作比较简答，即： \[ \begin{align*} n_x&=v_{1x} \times c − v_{1y} \times \sqrt{1-c^2}\\ n_y&=v_{1x} \times \sqrt{1-c^2}+ v_{1y} \times c \end{align*} \]
• 计算得到\(\hat{n}\)后，可以很方便的求出两个切点：从C1的圆心沿着\(\hat{n}\)方向，距离为\(r_1\)的点为C1的切点\(p_{ot1}\)，然后从\(p_{ot1}\)出发，沿着\(\vec{V_2}\)方向，与C2圆相交，得到切点\(p_{ot2}\)。

2、计算CSC曲线

CSC包括RSR、LSL、RSL、LSR，计算切点就是为了找到CSC曲线的“S”部分，计算CSC路径就变成了：从起点以最小转半径转弯到达第一个切点，直行到达第二个切点后，以最小转弯半径再次转弯，到达终点。

以RSR为例，假设起点为：\(s = (x_1,y_1,\theta_1)\)，终点为：\(g = (x_2,y_2,\theta_2)\)，\(C_1\)和\(C_2\)圆心计算方法为： \[ \begin{align*} p_{c1}&=(x_1 + r_{min} ∗ \cos(\theta_1 −\frac{π}{2}), y_1 + r_{min} ∗ \sin (\theta_1 -\frac{π}{2}))\\ p_{c2}&=(x_2 + r_{min} ∗ \cos(\theta_2 −\frac{π}{2}), y_2 + r_{min} ∗ \sin (\theta_2 -\frac{π}{2})) \end{align*} \]

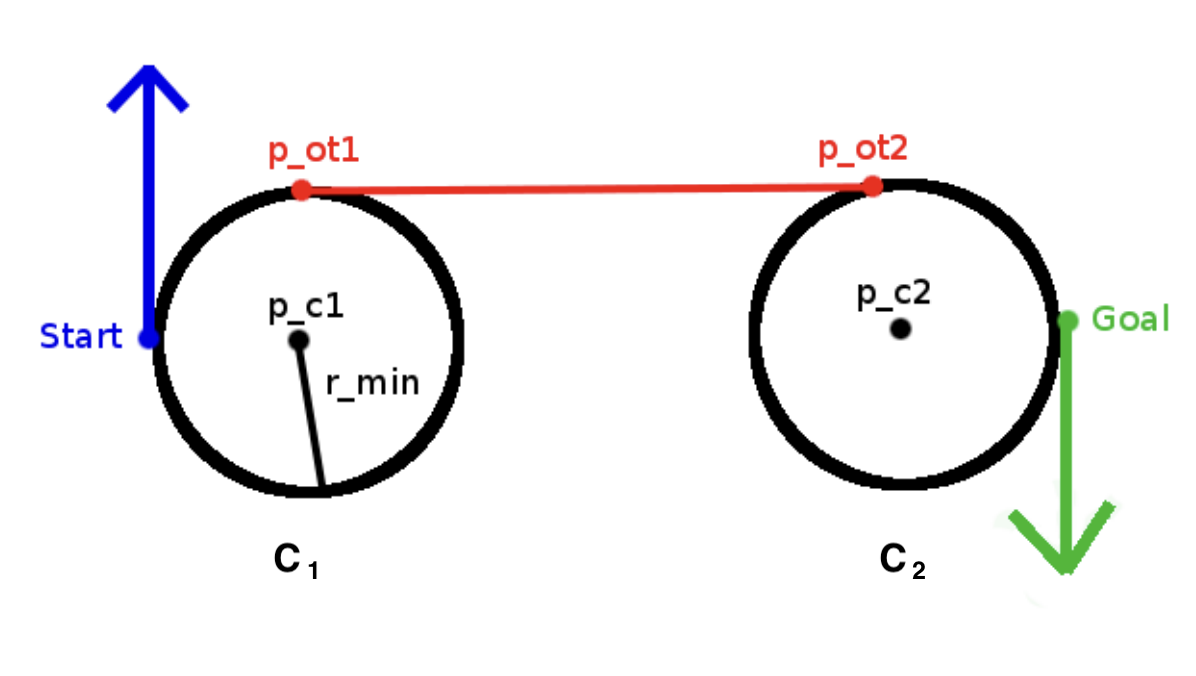
得到两个圆心后，就可以计算两个切点，从而得到车辆控制的三段轨迹：起始点到\(p_{ot1}\)的圆弧，\(p_{ot1}\)到\(p_{ot2}\)的线段和\(p_{ot2}\)到终点的圆弧。

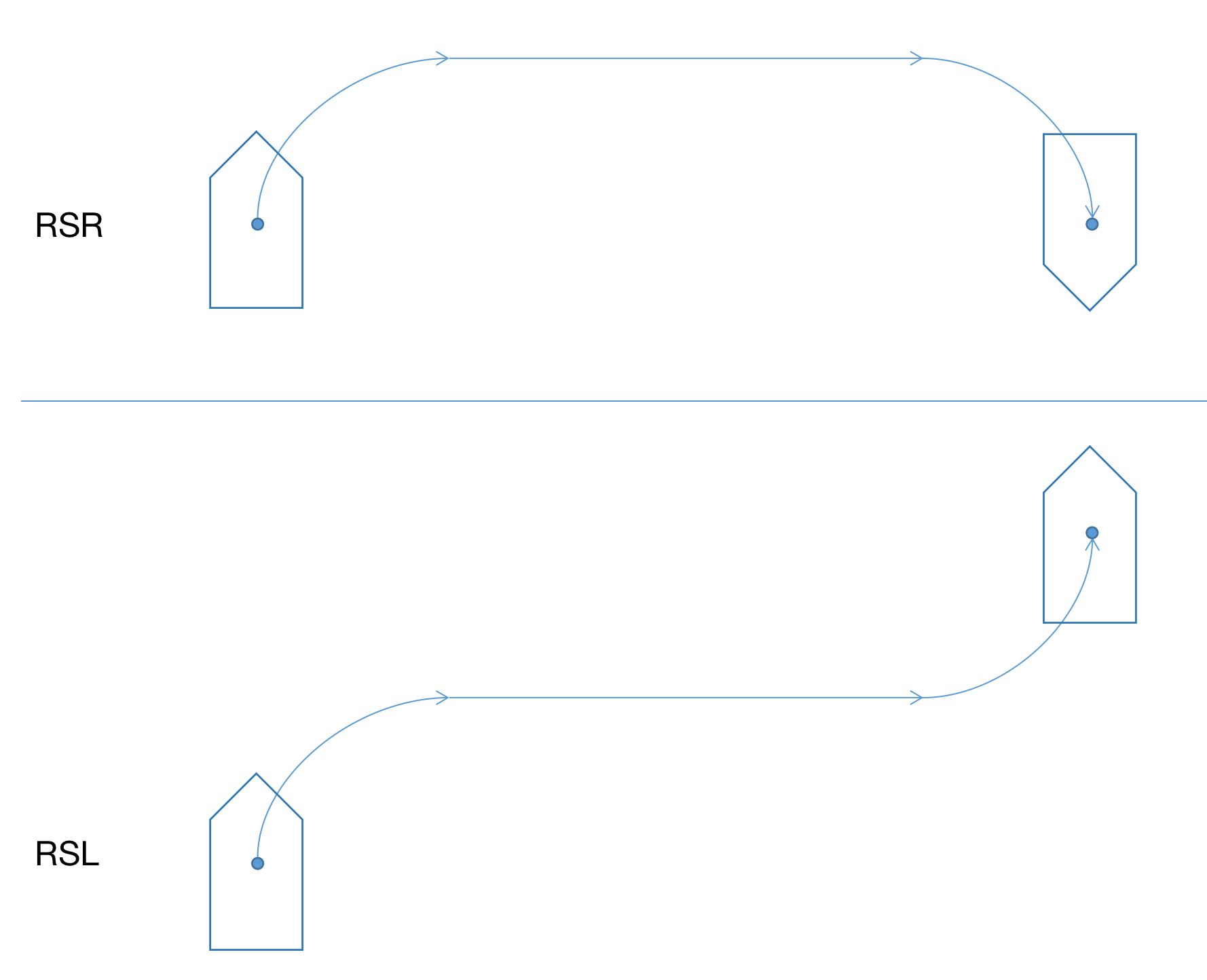
假设车辆速度恒定为1，起点为\(p_s = (x,y,\theta)\)，终点为\(p_e\)，\(T\)是从起点到达终点的时间，则根据车辆运动模型有： \[ \begin{align*} &\hat{x}(t)=\cos \theta(t)\\ &\hat{y}(t)=\sin \theta(t)\\ &\hat{\theta}(t)=\frac{1}{R} \end{align*} \] 其中\(R\)为转弯半径。

求解起点到终点的最短路径问题就是对下面问题的一个最优化过程： \[ \min Loss(p)=\int_0^T\sqrt{\hat{x}(t)^2+\hat{y}(t)^2}dt \] 由于\(\hat{x}(t)^2+\hat{y}(t)^2=1\), 即最短路径只与\(T\)有关。以RSR控制为例，就变成了3组控制：(-最大转向角,T1)、(0,T2)、(-最大转向角,T3)，实际实现时采取迭代式： \[ \begin{align*} x_{t+1} &= x_{t} + \delta ∗ \cos(\theta)\\ y_{t+1} &= y_{t} + \delta ∗ \sin(\theta)\\ \theta_{t+1} &= \theta_{t} +\frac{\delta}{R} \end{align*} \] 其中\(\delta\)取值一般为：\(\delta=[0.01,0.05]\)，给定弧长\(AR\)，有\(T_i=\frac{AR_i}{\delta}\)。

3、计算CCC

CCC包括RLR和LRL两种，不涉及到切线的计算。

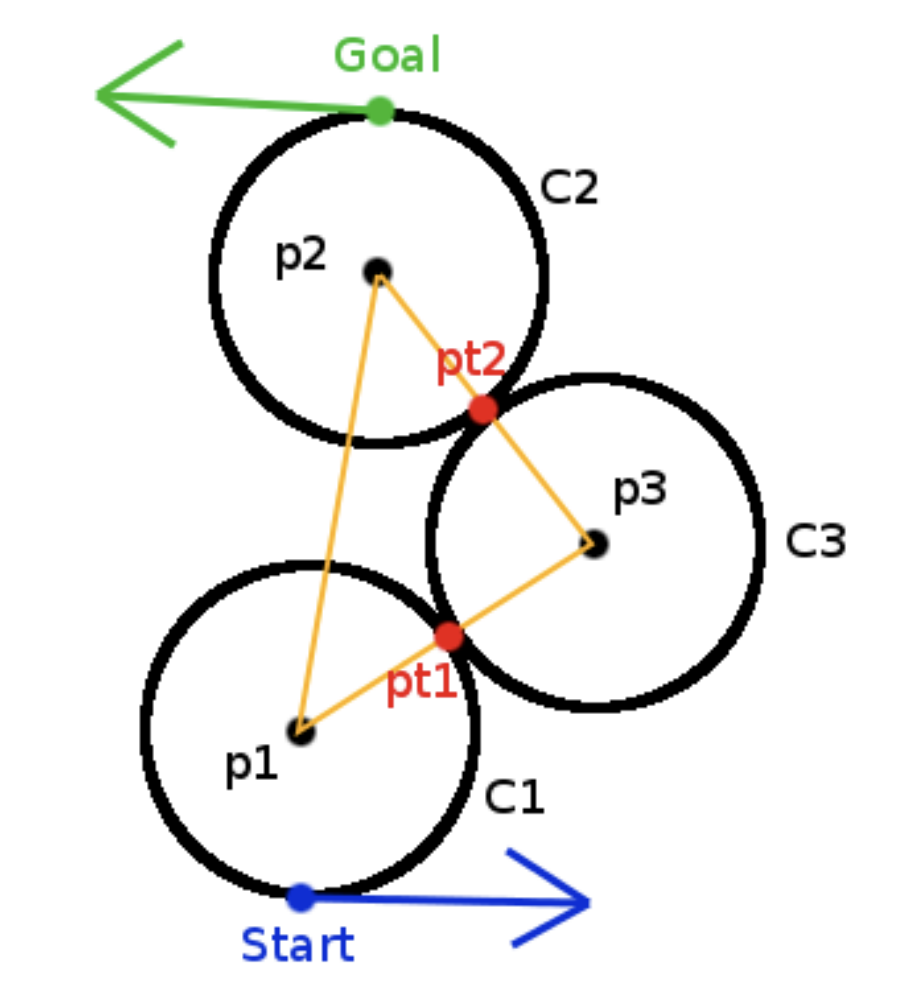
计算方法如下： \(p1, p2, p3\)分别为\(C1, C2, C3\)的圆心，\(C_3\)同时与\(C_1\)和\(C_2\)相切，\(r_{min}\)为最小转向半径， \[ \begin{align*} \overline{p_1p_3}&=\overline{p_2p_3}=2r_{min}\\ \overline{p_1p_2}&=D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\ \vec{V_1} &= p2−p1\\ \vec{V_2} &= p1−p3 \end{align*} \] 记\(\theta=\angle p_2 p_1 p_3\)，有： \[ \theta = \cos^{−1}(\frac{D}{4r_{min}}) \] 从而有： \[ p_3 = (x_1 + 2r_{min}\cos (\theta), y_1 + 2r_{min}\sin (\theta)) \] 注意：LRL模式时，\(\theta\)需要加上\(atan2(\vec{V_1})\)，RLR模式时，\(\theta\)需要减去\(atan2(\vec{V_1})\)。 对\(\vec{V_2}\)做缩放，有： \[ \vec{V_2}=\frac{\vec{V_2}}{||V_2||}*r_{min} \] 于是有： \[ p_{t1} = p_3 + \vec{V_2} \] \(p_{t2}\)的计算完全类似，这样三段弧线就得到了：\((x_1,y_1)\)到\(p_{t1}\)、\(p_{t1}\)到\(p_{t2}\)、\(p_{t2}\)到\((x_2,y_2)\)。

非线性最小二乘法控制

车辆的连续运动可以通过离散的多次运动做估计，假设有一个很小的时间间隔，车辆运动模型可以变为： \[ \begin{align*} &p_1(t+h)\approx p_1(t)+h\cdot v(t)\cos \theta(t)\\ &p_2(t+h)\approx p_2(t)+h\cdot v(t)\sin \theta(t)\\ &\theta(t+h)\approx \theta(t)+h\cdot\frac{v(t)}{L}\tan \phi(t) \end{align*} \]

定义输入向量：\(u_k=(v(k\cdot h),\phi(k\cdot h))\)，定义状态向量：\(x_k = (p_1(k\cdot h),p_2(k\cdot h),\theta(k\cdot h))\)，则运动模型可以表示为： \[ x_{k+1}=f(x_k,u_k)= \begin{bmatrix} (x_k)_1+h\cdot (u_k)_1\cos ((x_k)_3)\\ (x_k)_2+h\cdot (u_k)_1\sin ((x_k)_3)\\ (x_k)_3+h\cdot (u_k)_1\tan ((u_k)_2)/L \end{bmatrix} \]

其中\((u_k)_1\)代表向量\(u_k\)的第一个分量，其他的含义类似。于是车辆运动模型就变成了给定初始点、初始车身朝向和停止点，通过一定时间间隔变化产生一个输入序列，从而模拟车辆运行轨迹的过程，由于要求运动的最短路径，所以它是一个非线性约束最优化问题，希望每次迭代以最小的转向角和速度为代价，保持平稳的运动，最终得到代价最小的最优路径，数学描述如下： \[ \begin{align*} \min &\sum_{k=1}^N||u_k||^2+\gamma\sum_{k=1}^{N-1}||u_{k+1}-u_k||^2\\ s.t.&\quad x_2=f(0,u_1)\\ &\quad x_{k+1}=f(x_k,u_k),k=2,...,N-1\\ &\quad x_{final}=f(x_N,u_N) \end{align*} \] 其中：\(N\)为序列长度，\(u_1,...,u_N;x_1,...,x_N\)为变量。

参考文献

1、《A Comprehensive, Step-by-Step Tutorial on Computing Dubin’s Curves》

2、《Constrained nonlinear least squares》