 最优化是机器学习的永恒话题,本章主要对基于梯度或Hessian矩阵的最优化方法做了公式推导和原理方面的介绍。
最优化是机器学习的永恒话题,本章主要对基于梯度或Hessian矩阵的最优化方法做了公式推导和原理方面的介绍。
4. 最优化原理
4.1 泰勒定理
满足一定条件的函数可以通过泰勒展开式对其做近似:
4.1.1 泰勒展开式
泰勒展开式原理如下,主要采用分部积分推导: \[ \begin{align*} f(x+\Delta x)&=f(x)+\int_{x}^{x+\Delta x}\nabla f(t)dt\\ &=f(x)+((x+\Delta x) \nabla f(x+\Delta x)-xf(x))-\int_{x}^{x+\Delta x}t\nabla^2f(t)dt\\ &=f(x)+(x+\Delta x)(\nabla f(x)+\int_{x}^{x+\Delta x}\nabla^2f(t)dt)-x\nabla f(x)-\int_{x}^{x+\Delta x}t\nabla^2f(t)dt\\ &=f(x)+\nabla f(x)\Delta x +\int_{x}^{x+\Delta x}(x+\Delta x-t) \nabla^2f(t)dt\\ &......\\ &=f(x)+\nabla f(x)\Delta x+\frac{1}{2}\nabla^2 f(x)\Delta x^2+...\frac{1}{n!}\nabla^nf(x)\Delta x^n \\ &+ \int_{x}^{x+\Delta x}\frac{\nabla^{n+1}f(t)}{n!}(x+\Delta x-t) dt \end{align*} \]
4.1.2 泰勒中值定理
需要注意泰勒中值定理是一个严格的等式: \[ \begin{array}{l} f(x+\Delta x)=f(x)+\nabla f(x)\Delta x+\frac{1}{2}\nabla^2 f(x)\Delta x^2 + ...\frac{1}{n!}\nabla^nf(x)\Delta x^n \\ +\frac{1}{(n+1)!}\nabla^{n+1}f(\xi)\Delta x^{n+1} ,\text{where } \xi \in(0,\Delta x) \end{array} \]
4.2 梯度下降法
4.2.1 基本原理
梯度下降是一种简单、好用、经典的使用一阶信息的最优化方法(意味着相对低廉的计算成本),其基本原理可以想象为一个下山问题,当下降方向与梯度方向一致时,目标函数的方向导数最大,即此时目标函数在当前起点位置的下降速度最快。
1、一个小例子
假设有单变量实值函数\(y=f(x)\),其图形如下: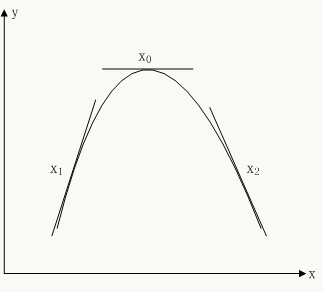
实值函数y=f(x)在点x_0的导数f'(x)的意义是该函数在x=x_0 处的瞬时变化率,即:
\(f'(x_0)=\lim_{\Delta x->0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\)
在自变量x发生微小变化时,目标函数值的变化可以这么描述:
\(dy=f'(x)dx\)
针对上图有以下三种情况:
(1)、\(x_1\)点位置,此时\(f'(x_1)>0\),在\(x_1\) 点做微小正向变化:\(dx>0\),显然有\(dy>0\),这说明在\(x_1\)点往\(x\)轴正向有可以使目标函数\(y=f(x)\)值增大点存在;
(2)、\(x_2\)点位置,此时\(f'(x_2)<0\),在\(x_2\) 点做微小负向变化:\(dx<0\),显然有\(dy>0\),这说明在\(x_2\)点往\(x\)轴负向有可以使目标函数\(y=f(x)\)值增大点存在;
(3)、\(x_0\)点位置,此时\(f'(x_0)=0\),不管在\(x_0\) 点做微小负向变化还是正向变化都有\(dy=0\),这说明在\(x_0\)点是一个最优解。
实际上,在一维情况下目标函数的梯度就是\(f'(x)\),它表明了目标函数值变化方向。
2、梯度与方向导数
方向导数 以二元函数:\(y=f(x_0,x_1)\)为例,设它在点\(p(x_0,x_1)\)的某个邻域\(U(p)\)内有定义,以点\(p(x_0,x_1)\)出发引射线l,\(p'(x_0+\Delta x_0,x_1+\Delta x_1)\)为\(l\)上的且在邻域\(U(p)\)内的任意点,则方向导数的定义为: \[\frac{\partial f}{\partial l} = \lim_{\rho->0^+} {\frac{f(x_0+\Delta x_0,x_1+\Delta x_1)-f(x_0,x_1)}{\rho}} \] 其中\(\rho\)表示\(p\)和\(p'\)两点之间的欧氏距离:\(\rho = \sqrt{(\Delta x_0)^2 + (\Delta x_1)^2}\) 从这个式子可以看到:方向导数与某个方向\(l\)有联系、方向导数是个极限值、方向导数与偏导数似乎有联系。 实际上,如果\(y=f(x_0,x_1)\)在点\(p(x_0,x_1)\)可微,则: \[\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x_0} \cos\alpha +\frac{\partial f}{\partial x_1} \cos\beta \] 其中\(\alpha\)和\(\beta\)分别是两个维度上的方向角 这里需要注意的一个细节是:沿某个维度的方向导数存在时,其偏导数不一定存在,原因就是方向导数只要求半边极限存在(\(\rho->{0^+}\)),而偏导数则要求双边都存在。
梯度 把方向导数变换一下形式: \[\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x_0} \cos\alpha +\frac{\partial f}{\partial x_1} \cos\beta =(\frac{\partial f}{\partial x_0}, \frac{\partial f }{\partial x_1}) \cdot (\cos\alpha, \cos\beta)\] 函数\(y=f(x_0,x_1)\)在点\(p(x_0,x_1)\)的梯度就被定义为向量: \[gradf(x_0,x_1)=\frac{\partial f}{\partial x_0}\cdot i + \frac{\partial f }{\partial x_1}\cdot j\] 与射线l同方向的单位向量被定义为: \(e=\cos \alpha \cdot i+ \cos \beta\cdot j\) 于是方向导数变成了: \[\frac{\partial f}{\partial l} = gradf(x_0,x_1)\cdot e=|gradf(x_0,x_1)|\cdot \cos<gradf(x_0,x_1), e>\] 我的理解是:方向导数描述了由各个维度方向形成的合力方向上函数变化的程度,当这个合力方向与梯度向量的方向相同时,函数变化的最剧烈,我想这就是为什么在梯度上升算法或者梯度下降算法中选择梯度方向或者负梯度方向的原因吧。换句话说就是:函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
![]()
某个函数和它的等高线,图中标出了a点的梯度上升方向
3、多维无约束问题
将开篇的那个小例子扩展到多维的情况,目标函数值将会成为一个向量,向任意个维度方向做微小变动都将对目标函数值产生影响,假设有n个维度,可以用下面的式子描述:
\[dy=(dy_0,....,dy_n)=grad f\cdot (dx_0,...,dx_n)^T=gradf\cdot dx=|grad f|\cdot |dx|\cdot \cos<grad f , dx>\]
令\(\alpha = \angle <grad f , dx>\)
(1)、当\(0\leq \alpha<\frac{\pi}{2}\),此时\(dy>0\),因此可以从点\(x\)移动使得目标函数值增加;
(2)、当\(\frac{\pi}{2}< \alpha\leq \pi\),此时\(dy<0\),因此可以从点\(x\)移动使得目标函数值减少;
(3)、当 \(\alpha=\frac{\pi}{2}\),梯度向量和\(dx\)正交(任一向量为0也视为正交),不管从点\(x\)怎样移动都找不到使目标函数值发生变化的点,于是x点就是目标函数的最优解。 由于\(dx\)可以是任意方向向量,只要点x的梯度向量不为零,从点x出发总可以找到一个变化方向使得目标函数值向我们希望的方向变化(比如就找梯度方向,此时能引起目标函数值最剧烈地变化),理论上当最优解\(x^*\)出现时就一定有\(gradf (x^*)=0\)(实际上允许以某个误差\(\epsilon\)结束),比如,对于梯度下降算法,当\(gradf (x^*)=0\)时迭代结束,此时的\(x^*\)为最优解(可能是全局最优解也可能是局部最优解) \[x_{n+1}=x_n - \alpha \cdot gradf(x_n)\]
总结来说,基于梯度的优化算法通常有两个核心元素:搜索方向和搜索步长,并且一般都会和泰勒定理有某种联系,从泰勒中值定理可以得到下面的等式:
\[ \begin{align*} f(x_{n+1})&=f(x_n)+\nabla f(x_n)(x_{n+1}-x_n)+\frac{1}{2}\nabla^2 f(\xi)(x_{n+1}-x_n)^2\\ &~~~~~~~~~~~~~~~\text{where } \xi \in(x_n,x_{n+1})\\ \because & \nabla f(x_{n+1})=g_n+\nabla^2\\ &f(\xi)(x_{n+1}-x_n)=0\\ \therefore & x_{n+1}=x_n-\underbrace{\nabla^2 f(\xi)^{-1}}_{\eta :~\text{learning rate }} \underbrace{\nabla f(x_n)}_{ d:~\text{gradient}}\\ \end{align*} \]
抽象出迭代框架如下:
\[ \begin{align*} x_{n+1}&=x_n-\eta \nabla f(x_n)\\ &~~~~~~~~\text{ where $f(x)$ is objective function.}\\ &or\\ x_{n+1}&=x_n-\Delta x_n\\ \Delta x_n&=\eta \nabla f(x_n) \end{align*} \]
4.2.2 拉格朗日乘数法和KKT条件
假设目标函数和约束在某点可微,用符号\(\nabla f\)代替符号\(grad f\)。
1、等式约束
\[\begin{eqnarray*} &&\min f(x) \\ &&s.t. h(x)=0, \quad \end{eqnarray*}\]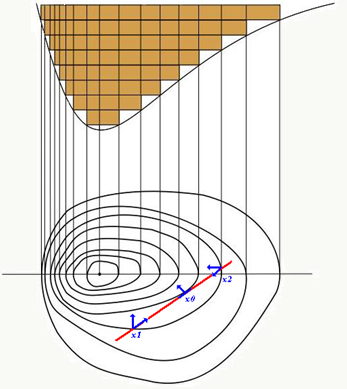
在约束条件的作用下,与点\(x\)(它是个向量)可移动方向相关的向量\(dx\)就不像无约束问题那样随便往哪个方向都能移动了,此时\(dx\)只能沿着约束曲线移动,例如,在\(x1\)、\(x2\)处,\(\nabla f(x)\)和\(dx\)不正交,说明还有使目标函数值更小的等高线存在,所以点\(x\)还有移动的余地,当移动到\(x0\)位置时\(\nabla f(x)\)和\(dx\)正交,得到最优解\(x0\)。那么在最优解处\(\nabla f(x)\)和约束有什么关系呢?因为此时\(h(x)=0\),\(\nabla h(x) \cdot dx=0\),显然此时有\(\lambda \cdot \nabla h(x)=\nabla f(x)\)(其中\(\lambda\)是常数),也就是说约束的梯度向量与目标函数的梯度向量在最优解处一定平行。 想到求解此类优化问题时最常用的方法——拉格朗日乘数法,先要构造拉格朗日函数:
\[L(x,\lambda) = f(x) - \lambda h(x) \] 其中\(\lambda \geq0\),是常数
为什么求解拉格朗日函数得到的最优解就是原问题的最优解呢?
\[\frac{\partial L(x,\lambda)}{\partial x}=\nabla f(x)-\lambda \nabla h(x) \frac{\partial L(x,\lambda)}{\partial \lambda}= h(x)\]
假设\(x^*\)、\(\lambda^*\)为\(L(x,\lambda)\)的最优解,那么就需要满足:
\[ \begin{eqnarray*} \\ \nabla f(x^*)-\lambda^* \nabla h(x^*)&=& 0\\ \\ h(x^*)&=&0\\ \end{eqnarray*} \]
第一个式子印证了约束的梯度向量与目标函数的梯度向量在最优解处一定平行,第二个式子就是等式约束本身。
于是:
\[ \begin{eqnarray*} &&L(x,\lambda) &\geq &L(x^*,\lambda^*)\\ \Rightarrow&& f(x)-\lambda h(x) &\geq &f(x^*)-\lambda^* h(x^*) \\ \Rightarrow &&f(x) &\geq & f(x^*) \end{eqnarray*} \]
2、不等式约束
实际情况中,约束条件可能是等式约束也可能是不等式约束或者同时包含这两种约束,下面描述为更一般地情况:
\[ \begin{eqnarray*} & \min &f(x)\\ & s.t.& h_i(x)=0 \quad (i=0 ... n)\\ &&g_j(x) \leq 0 \quad (j=0...m) \end{eqnarray*} \]
依然使用拉格朗日乘数法,构造拉格朗日函数:
\[L(x,\alpha ,\beta) = f(x) + \sum\limits_{i=0}^n \alpha_i \cdot h_i(x) + \sum\limits_{j=0}^m \beta_j\cdot g_j(x) \] 其中\(\alpha_i \geq 0\)且\(\beta_j \geq 0\)
在这里不得不说一下Fritz John 定理了,整个证明就不写了(用局部极小必要条件定理、Gordan 引理可以证明)。
定理1:
依然假设\(x^*\)为上述问题的极小值点,问题中涉及到的各个函数一阶偏导都存在,则存在不全为零的_i使得下组条件成立:
\[ \lambda_0 \nabla f(x^*) + \sum\limits_{i=0}^n \lambda_i \cdot \nabla h_i(x^*) + \sum\limits_{j=0}^m \lambda_j\cdot \nabla g_j(x^*)=0 \lambda_j \cdot g_j(x^*) = 0 ,j=0,...m \lambda_j \geq 0,j=0,...m\]
这个定理第一项的形式类似于条件极值必要条件的形式,如果\(\lambda_0=0\)则有效约束 \(\nabla g_j(x)\)会出现正线性相关,由Gordan 引理知道此时将存在可行方向,就是\(x^*\)将不是原问题的极值点,因此令 \(\nabla g_j(x)\)则线性无关则\(\lambda_0>0\) 。
\(\lambda_j \cdot g_j(x^*) = 0 ,j=1,...m\)这个条件又叫互不松弛条件(Complementary Slackness),SVM里的支持向量就是从这个条件得来的。
由Fritz John 定理可知 \(\nabla g_j(x)\)线性无关则\(\lambda_0>0\) ,让每一个拉格朗日乘子除以\(\lambda_0\),即\(\mu_i=\lambda_i/\lambda_0\),得到下面这组原问题在点\(x^*\)处取得极小值一阶必要条件。
定理2:
假设\(x^*\)为上述问题的极小值点,问题中涉及到的各个函数一阶偏导都存在,有效约束 \(\nabla g_j(x)\)线性无关,则下组条件成立:
\[\frac{\partial L(x,\mu_i,\mu_j)}{\partial x} =\nabla f(x^*) + \sum\limits_{i=0}^n \mu^*_i \cdot \nabla h_i(x^*) + \sum\limits_{j=0}^m \mu^*_j\cdot \nabla g_j(x^*)=0 \\ \mu_j^* \cdot g_j(x^*) = 0 ,j=0,...m \\ \mu^*_j \geq 0,j=0,...m \\ h_i(x^*)=0,i=0,..,n \\ g_j(x^*) \leq 0,j=0,...m\]
这组条件就是Karush-Kuhn-Tucker条件,满足KKT条件的点就是KKT点,需要注意的是KKT条件是必要条件(当然在某些情况下会升级为充要条件,比如凸优化问题)。 由此也可以想到求解SVM最大分类间隔器时,不管是解决原问题还是解决对偶问题,不管是用SMO方法或其它方法,优化的过程就是找到并优化违反KKT条件的最合适的乘子。 KKT条件与对偶理论有密切的关系,依然是解决下面这个问题:
\[ \begin{eqnarray*} & \min &f(x)\\ & s.t.& h_i(x)=0 \quad (i=0 ... n)\\ &&g_j(x) \leq 0 \quad (j=0...m) \end{eqnarray*} \]
构造拉格朗日函数:
\[ L(x,\alpha ,\beta) = f(x) + \sum\limits_{i=0}^n \alpha_i \cdot h_i(x) + \sum\limits_{j=0}^m \beta_j\cdot g_j(x)\] 其中\(\alpha_i \geq 0\)且\(\beta_j \geq 0\),它们都是拉格朗日乘子
令\(O_p(x)=\max\limits_{\alpha ,\beta} L(x,\alpha,\beta)\),原问题可以表示为下面这个形式:
\[ O_p(x)= \left\{ \begin{array}{c} &f(x)& if \quad x \quad satisfies \quad primal \quad constraints&\\ & \infty& otherwise.&\\ \end{array} \right. \]
这个式子比较容易理解,当x违反原问题约束条件时有:
\[ O_p(x)=\max\limits_{\alpha ,\beta} L(x,\alpha ,\beta) = \max\limits_{\alpha, \beta} f(x) + \sum\limits_{i=0}^n \alpha_i \cdot h_i(x) + \sum\limits_{j=0}^m \beta_j\cdot g_j(x)=\infty \]
于是原问题等价为下面这个问题:
\[ \min\limits_x O_p(x)=\min\limits_x \max\limits_{\alpha ,\beta} L(x,\alpha,\beta) \] 它的最优解记为\(p^*\)
令\(O_d(\alpha,\beta)=\min\limits_{x} L(x,\alpha,\beta)\),则有以下形式:
\[\max\limits_{\alpha,\beta} O_d(\alpha,\beta)=\max\limits_{\alpha,\beta} \min\limits_{x} L(x,\alpha,\beta)\]
它的最优解记为\(d^*\),上面这两个形式很像,区别只在于\(min\)和\(max\)的顺序,实际上\(O_p(x)\)和\(O_d(\alpha,\beta)\)互为对偶问题。
因为\(\max\min \leq \min \max\),打个不太恰当的比喻,这就像瘦死的骆驼比马大,具体的证明就不写了;
所以\(d^* \leq p*\),这个就是弱对偶性,此时存在对偶间隙,它被定义为:\(gap=p^*-d^*\)。
有弱对偶性就有强对偶性,它指的是在某些条件下有\(d^* = p*\),比如在以下条件下满足强对偶性:
目标函数和所有不等式约束函数是凸函数,等式约束函数是仿射函数(形如\(y=w^tx+b\)),且所有不等式约束都是严格的约束(大于或小于)。
KKT条件和强对偶性的关系是:
KKT条件是强对偶性成立的必要条件,特别的,当原问题是凸优化问题时,KKT条件就是充要条件,强对偶性存在时KKT点既是原问题的解也是对偶问题的解,这个时候对偶间隙为0。
4.2.3 批量梯度下降
按照上面等式,每次迭代,为计算梯度值都需要把所有样本扫描一遍,收敛曲线类似下图:
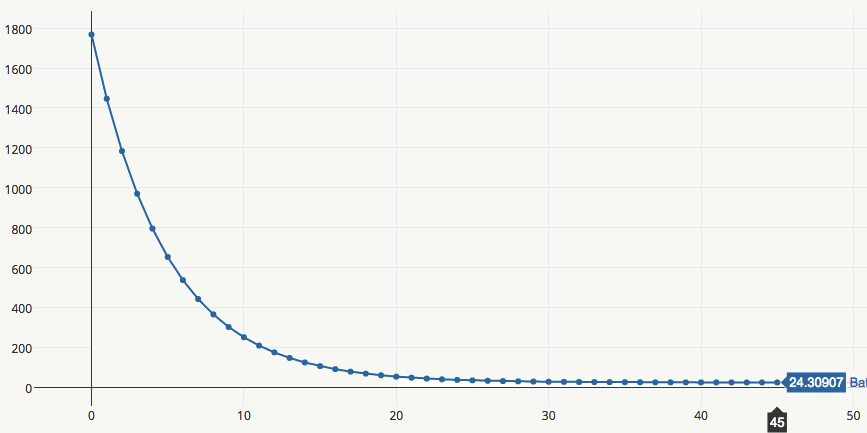
它的优点如下: - 模型学习与收敛过程通常是平滑的和稳定的; - 关于收敛条件有成熟完备的理论; - 针对它有不少利用二阶信息加速收敛的技术,例如conjugate gradient; - 对样本噪声点相对不敏感。
它的缺点如下:
- 收敛速度慢;
- 对初始点敏感;
- 数据集的变化无法被学习到; captured.
- 不太适用于大规模数据。
4.2.4 随机梯度下降
完全随机梯度下降(Stochastic Gradient Descent,可以想想这里为什么用Stochastic而不用Random?)每次选择一个样本更新权重,这样会带来一些噪声,但可能得到更好的解,试想很多问题都有大量局部最优解,传统批量梯度下降由于每次收集所有样后更新梯度值,当初始点确定后基本会落入到离它最近的洼地,而随机梯度下降由于噪声的引入会使它有高概率跳出当前洼地,选择变多从而可能找到更好的洼地。 收敛曲线类似下图:
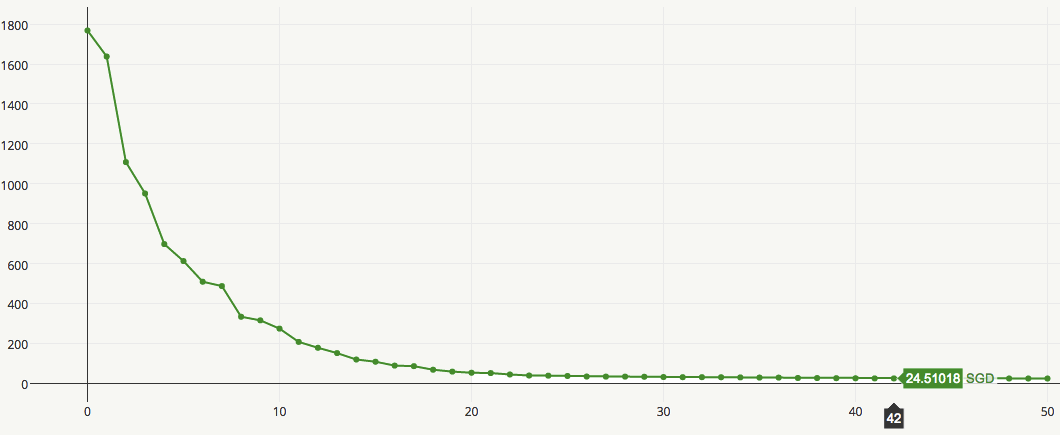
完全随机梯度下降和批量梯度下降的优缺点几乎可以互换: - SGD的收敛速度更快; - SGD相对来说对初始点不敏感,容易找到更优方案; - SGD相对适合于大规模训练数据; - SGD能够捕捉到样本数据的变化; - 噪声样本可能导致权重波动从而造成无法收敛到局部最优解,步长的设计对其非常重要。
实践当中,很多样本都有类似的模式,所以SGD可以使用较少的抽样样本学习得到局部最优解,当然完全的批量学习和完全的随机学习都太极端,所以往往采用对两者的折中。
4.2.5 小批量梯度下降
小批量梯度下降(Mini-batch Gradient Descent)是对SGD和BGD的折中,采用相对小的样本集学习,样本集大小随着学习过程保持或逐步加大,这样既能有随机带来的好处,又能使用二阶优化信息加速收敛,目前主流机器学习工具几乎都支持小批量学习。 小批量学习收敛过程如下:
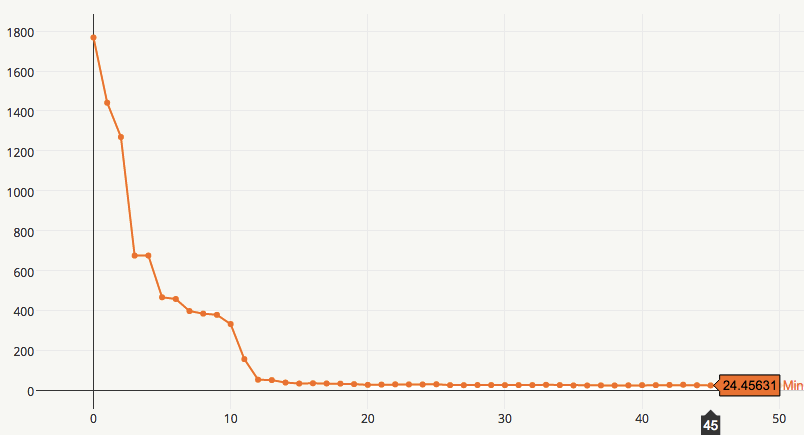
梯度下降的另外一个任务是寻找合适的学习率,关于它有很多方法,介绍如下:
4.2.6 牛顿法
从泰勒展开式可以得到带最优步长的迭代式:
\[ \begin{array}{l} \Delta x_n=-\nabla^2 f(\xi)^{-1}\nabla f(x_n)\\ x_{n+1}=x_n+\Delta x_n \end{array} \]
但最优的学习率需要计算hessian矩阵,计算复杂度为\(O(n^3)\),所以这种方法不怎么用。
为方便起见,使用 \(g_n\) 代替 \(\nabla f(x_n)\).
4.2.7 Momentum
SGD的一大缺点是\(\Delta x_n\) 只和当前样本有关系,如果样本存在噪声则会导致权重波动,一种自然的想法就是即考虑历史梯度又考虑新样本的梯度:
\[ \begin{array}{l} \Delta x_n=\rho \Delta x_{n-1}-\eta g_n\\ x_{n+1}=x_n+\Delta x_n\\ \rho \text{ is usually set to a small value }\le 0.9 \end{array} \]
对动量的运行过程说明如下:
在初始阶段,历史梯度信息会极大加速学习过程(比如n=2时);
当准备穿越函数波谷时,差的学习率会导致权重向相反方向更新,于是学习过程会发生回退,这时有动量项的帮助则有可能越过这个波谷;
最后在梯度几乎为0的时候,动量项的存在又可能会使它跳出当前局部最小值,于是可能找到更好的最优值点。
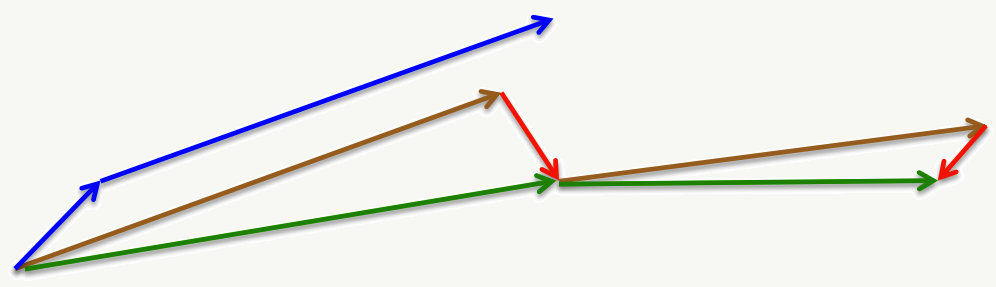
\[ \begin{array}{l} \Delta x_n=\rho \Delta x_{n-1}-\eta \nabla f(x_n-\rho \Delta x_{n-1})\\ x_{n+1}=x_n+\Delta x_n\\ \rho \text{ is usually set to a small value }\le 0.9 \end{array} \]
4.2.8 AdaGrad
Adagrad同样是基于梯度的方法,对每个参数给一个学习率,因此对于常出现的权重可以给个小的更新,而不常出现的则给予大的更新,于是对于稀疏数据集就很有效,这个方法常用于大规模神经网络,Google的FTRL-Proximal也使用了类似方法,可参见:Google Ad Click Prediction a View from the Trenches和Follow-the-Regularized-Leader and Mirror Descent: Equivalence Theorems and L1 Regularization。
\[ \begin{array}{l} \Delta x_n=-\frac{\eta}{\sqrt{\sum_{i=1}^{n}g_i^2}+\beta}g_n\\ x_{n+1}=x_n+\Delta x_n\\ \beta \text{ is usually set to a small value.} \end{array} \]
这个方法有点像L2正则,其运作原理如下:
在学习前期,梯度比较小regularizer比较大,所以梯度会被放大;
在学习后期,梯度比较大regularizer比较小,所以梯度会被缩小。
但它的缺点是,当初始权重过大或经过几轮训练后会导致正则化太小,所以训练将被提前终止。
4.2.9 AdaDelta
Adadelta是对Adagrad的改进,解决了以下短板:
经过几轮的训练会导致正则化太小;
需要设置一个全局学习率;
当我们更新\(\Delta x\),等式左边和右边的单位不一致。
对于第一个短板,设置一个窗口\(w\),仅使用最近几轮的梯度值去更新正则项但计算\(E[\nabla f(x)_{1\sim n}]\) 太复杂,所以使用类似动量法的策略:
\[ \begin{array}{l} E[g^{2}]_{n}=\rho E[g^{2}]_{n-1}+(1-\rho )g_{n}^{2}\\ \Delta x_n=-\frac{\eta}{\sqrt{E[g^2]_n+\beta}}g_n\\ x_{n+1}=x_n+\Delta x_n\\ \beta \text{ is usually set to a small value.}\\ \rho \text{ is decay coefficient.} \end{array} \]
对其他短板,AdaDelta通过以下方法解决。
对SGD与Momentum(里面的注释是理解这个变换的关键):
\[ \text{unit of }\Delta x \propto \text{unit of }g \propto \frac{\partial f}{\partial x} \propto \frac{1}{\text{unit of }x}\\ (\text{When $f$ is negative log likelihood function }\frac{\partial f}{\partial x} \propto \frac{\partial logf}{\partial x} =\frac{\frac{\partial f}{\partial x}}{f}) \]
对牛顿法: \[ \text{unit of }\Delta x \propto \text{unit of }H^{-1}g\propto \frac{\frac{\partial f}{\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}\propto \frac{\frac{1}{x}}{\frac{1}{x}.\frac{1}{x}}\propto \text{unit of }x \]
所以二阶方法有正确的单位且快于一阶方法。
来源于Becker 和 LeCuns' 的hessian估计法:
\[ \begin{array}{l} \Delta x_{n} \approx \frac{\frac{\partial f}{\partial x}}{\frac{\partial^{2}f}{\partial x^{2}}}=\frac{1}{\frac{\partial^{2}f}{\partial x^{2}}}\cdot \frac{\partial f}{\partial x}=\frac{1}{\frac{\partial^{2}f}{\partial x^{2}}}\cdot g_n\\ define:RMS[g]_{n}=\sqrt{E[g^{2}]_{n}+\epsilon }\\ \because \frac{1}{\frac{\partial^{2}f}{\partial x^{2}}}=\frac{\Delta x}{\frac{\partial f}{\partial x}}\approx -\frac{RMS[\Delta x]_{n-1}}{RMS[g]_{n}}\\ \therefore \Delta x_{n}=-\frac{RMS[\Delta x]_{n-1}}{RMS[g_n]}\cdot g_n \end{array} \]
完整的算法描述如下:
对以上算法的比较如下:
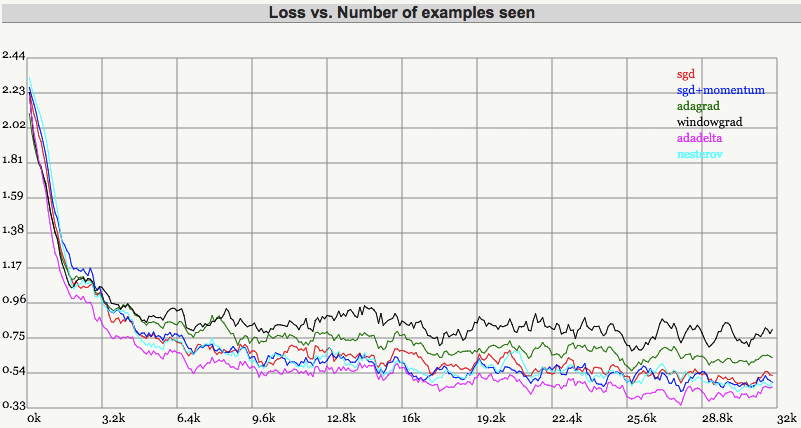
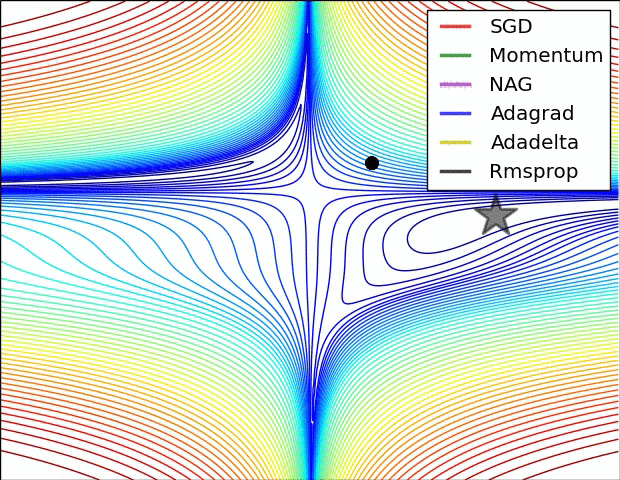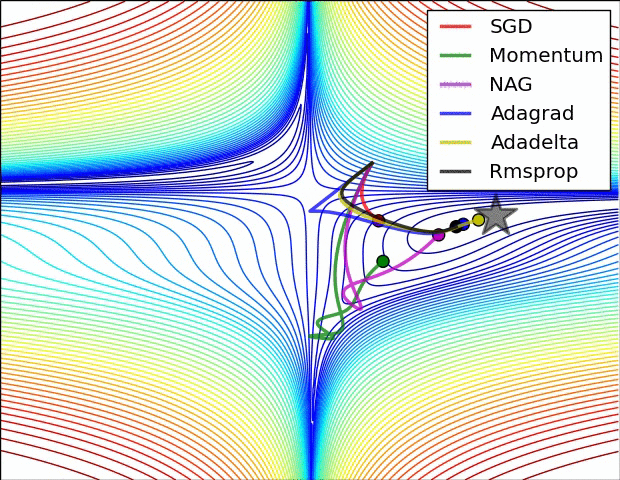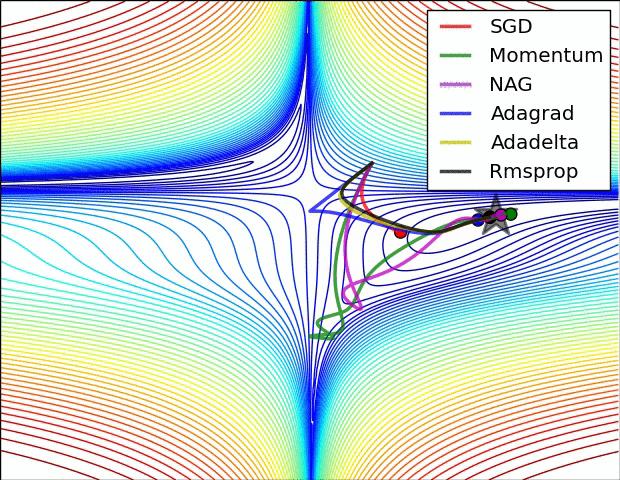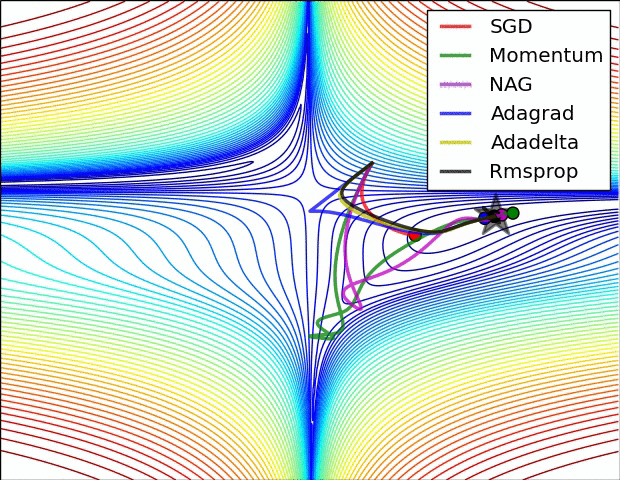
4.2.10 Adam
Adam是对Adadelta的改进,原理如下:
\[ \begin{align*} &Recall: \Delta x_n=-\frac{\eta}{\sqrt{\sum_{i=1}^{n}g_i^2}+\epsilon}g_n\\ &\text{Keeping an exponentially decaying average of past gradients:}\\ &m_n = \beta_1 m_{n-1} + (1 - \beta_1) g_n\\ &v_n = \beta_2 v_{n-1} + (1 - \beta_2) g_n^2\\ &\because m_n=(1-\beta_1)\sum_{i=1}^n\beta_1^{n-i}g_i\\ &~~~~v_n=(1-\beta_2)\sum_{i=1}^n\beta_2^{n-i}g_i^2\\ &\therefore E[m_n]=E[(1-\beta_1)\sum_{i=1}^n\beta_1^{n-i}g_i]=E[g_n](1-\beta_1^n)\\ &~~~~E[v_n]=E[g_n^2](1-\beta_2^n)\\ &\\ &\text{if set: }\\ &\hat{m}_n = \dfrac{m_n}{1 - \beta^n_1}\\ &\hat{v}_n = \dfrac{v_n}{1 - \beta^n_2}\\ &\text{then we get the bias-corrected first and second moment estimates: }\\ &E[\hat{m_n}]=m_n \text{ and } E[\hat{v_n}]=v_n\\ &\\ &\text{So the equation is:}\\ &\Delta x_n=- \dfrac{\eta}{\sqrt{\hat{v}_n} + \epsilon} \hat{m}_n\\ &x_{n+1} = x_{n} +\Delta x_n\\ &\text{The authors propose default values of 0.9 for $\beta_1$, 0.999 for $\beta_2$, and $10^{-8}$ for $\epsilon$.} \end{align*} \]
算法伪代码如下:
4.3 并行SGD
SGD相对简单并且被证明有较好的收敛性质和精度,所以自然而然就想到将其扩展到大规模数据集上,就像Hadoop/Spark的基本框架是MapReduce,并行机器学习的常见框架有两种: AllReduce 和 Parameter Server(PS)。
4.3.1 AllReduce
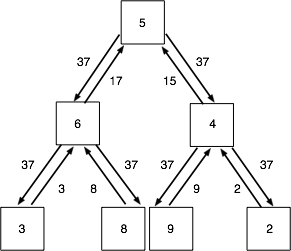
AllReduce的思想来源于MPI,它可以被看做Reduce操作+Broadcast操作,例如:
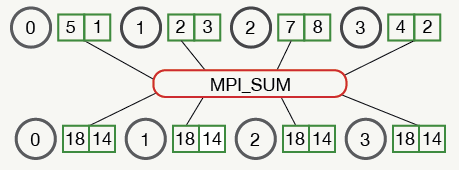
其他AllReduce的拓扑结构如下:
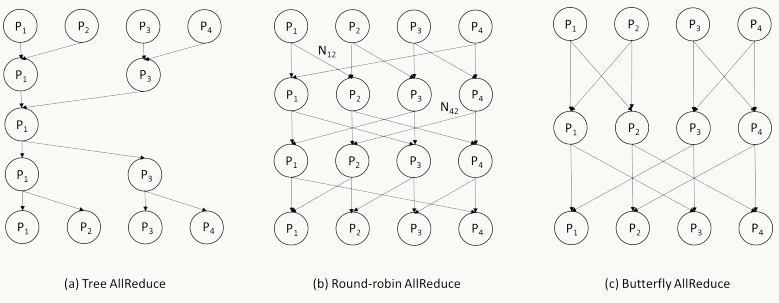
使用mini-batch的并行SGD算法伪代码如下:
\[ \begin{array}{l} \text{Algorithm 2: parallelizing SGD with mini-batch}\\ \text{If we have examples $X=\{x_0,x_1,...x_m\}$, machines $n$, threads of each machine $p$,} \\ \text{iterations T, batch b, local iterations t.}\\ \\ \textbf{Require}:\eta>0,m>1,n>1,p>1,T>0,b>1,t>0\\ \quad1.\;\;\;\;\textbf{define}~H=\lfloor \frac{m}{n} \rfloor,h=\lfloor \frac{H}{p} \rfloor\\ \quad2.\;\;\;\;\text{randomly partition examples $X$,giving $H$ examples to each machine}\\ \quad3.\;\;\;\;w=0\\ \quad4.\;\;\;\;\textbf{for all }i = 1, ... T \text{ and $w$ not convenged} \textbf{ do}\\ \quad5.\;\;\quad\quad\textbf{for all }j \in \{1, ..., n\} \textbf{ parallel do}\\ \quad6.\;\;\quad\quad\quad\quad\text{randomly partition examples $h$ on machine j to each thread.}\\ \quad7.\;\;\quad\quad\quad\quad\textbf{for all }k \in \{1, ..., p\} \textbf{ parallel do}\\ \quad8.\;\;\quad\quad\quad\quad\quad\quad\text{randomly shuffle examples on thread k}\\ \quad9.\;\;\quad\quad\quad\quad\quad\quad w_0^k=0\\ \quad10.\quad\quad\quad\quad\quad\quad\textbf{for all }q = 1, ... t \textbf{ do}\\ \quad11.\quad\quad\quad\quad\quad\quad\quad\quad \textbf{choose }\text{examples $b$ uniformly at random}\\ \quad12.\quad\quad\quad\quad\quad\quad\quad\quad \textbf{update }w_{q+1}^k=w_{q}^k+\eta g_q^k\\ \quad13.\quad\quad\quad\quad\textbf{reduce }w_j=\frac{1}{p}\sum_{k=1}^p w_q^k\\ \quad14.\quad\quad\textbf{AllReduce (reduce $w_j$)}\\ \quad15.\quad\quad w=\frac{1}{n}\sum_{i=1}^n w_j^i\\ \quad16.\quad\quad\textbf{AllReduce (broadcast $w$)}\\ \quad17.\quad\textbf{return }w \end{array} \]
4.3.2 参数服务器(Parameter Server)
参数服务器强调模型训练时参数的并行异步更新,最早是由Google的Jeffrey Dean团队提出,为了解决深度学习的参数学习问题,其基本思想是:将数据集划分为若干子数据集,每个子数据集所在的节点都运行着一个模型的副本,通过独立 部署的参数服务器组织模型的所有权重,其基本操作有:Fatching:每隔n次迭代,从参数服务器获取参数权重,Pushing:每隔m次迭代,向参数服务器推送本地梯度更新值,之后参数服务器会更新相关参数权重,其基本架构如下: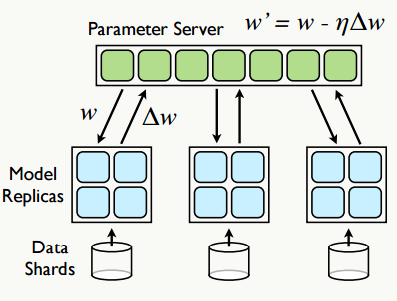
每个模型的副本都是,为减少通信开销,每个模型副本在迭代\(n_{fetch}\)次后向参数服务器请求参数跟新,反过来本地模型每迭代\(n_{push}\)次后向参数服务器推送一次梯度更新值,当然,为了折中速度和效果,梯度的更新可以选择异步也可以是同。 参数服务器是一个非常好的机器学习框架,尤其在深度学习的应用场景中,有篇不错的文章: 参数服务器——分布式机器学习的新杀器。开源的实现中比较好的是bosen项目和李沐的ps-lite(现已集成到DMLC项目中)。
下面是一个Go语言实现的多线程版本的参数服务器(用于Ftrl算法的优化),源码位置:Goline:
1 | // data structure of ftrl solver. |
4.4 二阶优化方法
4.4.1 概览
大部分的优化算法都是基于梯度的迭代方法,其迭代式来源为泰勒展开式,迭代的一般式为:
\[ \begin{array}{l} x_{k+1}=x_{k}+\alpha_kp_k \end{array} \]
其中\(\alpha_k>0\) 被称作步长,向量\(p_k\) 被称作搜索方向,它一般要求是一个能使目标函数值(最小化问题)下降的方向,即满足:
\[ \begin{array}{l} p_{k}^T\nabla f(x_k)<0 \end{array} \]
进一步说,\(p_k\) 的通项式有以下形式:
\[ \begin{array}{l} p_{k}=-B_{k}^{-1}\nabla f(x_k) \end{array} \]
\(B_k\) 是一个对称非奇异矩阵(大家请问为什么?)。
在 Steepest Descent 法中 \(B_k\) 是一个单位矩阵;
在 Newton 法中,\(B_k\) 是一个精确的Hessian 矩阵 \(\nabla^2 f(x_k)\);
在 Quasi-Newton 法中, \(B_k\) 是对Hessian矩阵的估计。
\[ \begin{array}{l} \because p_{k}^T\nabla f(x_k)=-\nabla f(x_k)^TB_{k}^{-1}\nabla f(x_k)<0\\ \therefore \text{$B_k$ is must positive definite.} \end{array} \]
这类优化方法大体分两种,要么是先确定优化方向后确定步长(line search),要么是先确定步长后确定优化方向(trust region)。

以常用的line search为例,如何找到较好的步长 \(\alpha\)呢?好的步长它需要满足以下条件:
- Armijo 条件
充分下降条件,即要使步长\(\alpha_k\)在非精确一维搜索中能保证目标函数 \(f\)下降,则它需要满足以下不等式:
\(f(x_k+\alpha p_k) \le f(x_k) + c_1\alpha \nabla f_k^Tp_k\)
\(c_1\) 一般选取一个较小的值,例如:\(c_1=10^{−4}\)。
Armijo 条件的几何解释如下:
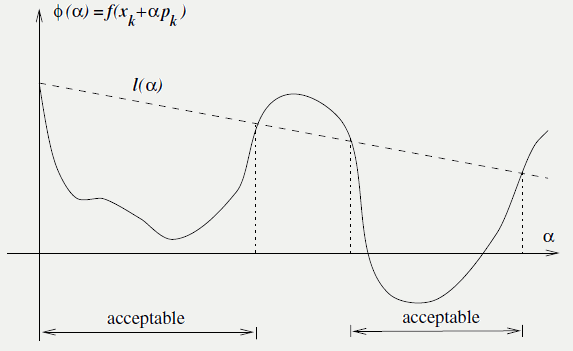
常用求解方法如下:
\[ \begin{array}{l} \text{Algorithm 3.Backtracking Line search}\\ \textbf{Require:}\;\; \rho \in (0,1), c \in (0,1)\\ \quad1.\;\;\textbf{choose }\hat{\alpha}>0,\text{set $\alpha=\hat{\alpha}$}\\ \quad2.\;\;\textbf{repeat }\text{until }f(x_k+\alpha p_k) \le f(x_k) + c\alpha \nabla f_k^Tp_k\\ \quad3.\quad\quad\alpha=\rho\alpha\\ \quad4.\;\;\textbf{end(repeat)}\\ \quad5.\;\;\text{return }\alpha \end{array} \]
- Curvature 条件
不只要求步长能使目标函数下降,还要求其程度,这个要求有点严格,一般只要做到Armijo条件就好了,不等式如下:
\(\nabla f(x_k+\alpha p_k)^Tp_k \ge c_2 \nabla f_k^Tp_k, c_2 \in(c_1,1)\)
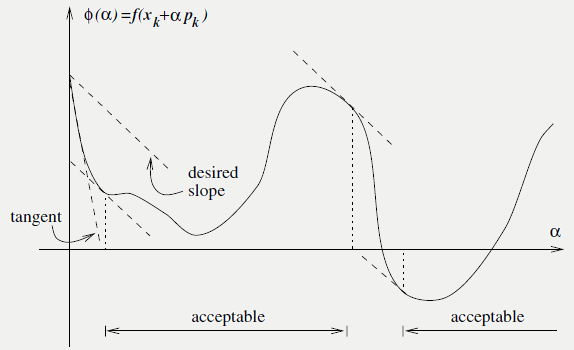
- Wolfe 条件
步长同时满足Armijo 条件和Curvature 条件则被称为其满足Wolfe 条件。
4.4.2 牛顿法(Newton Method)
以\(x_0\)点开始寻找\(f(x)=0\)的解,在该点做切线,得到新的起点: \(x_1=x_0-\frac{f(x_0)}{f'(x_0)}\)
迭代,直到满足精度条件得到\(f(x)=0\)的最优解.
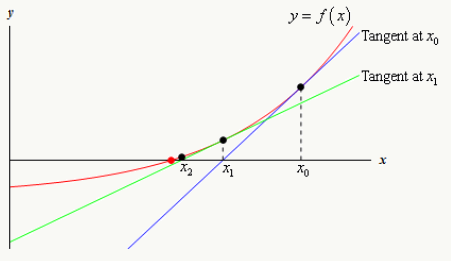
从泰勒展开式得到牛顿法的基本迭代式:
\[ \begin{array}{l} f(x_{n+1})=f(x_n)+\nabla f(x_n)(x_{n+1}-x_n)+\frac{1}{2}\nabla^2 f(x_n)(x_{n+1}-x_n)^2\\ \because \nabla f(x_{n+1})=\nabla f(x_n)+\nabla^2 f(x_n)(x_{n+1}-x_n)=0\\ \therefore x_{n+1}=x_n-\nabla^2 f(x_n)^{-1}\nabla f(x_n)\\ \end{array} \]
对牛顿法的改进之一是使用自适应步长 \(\alpha\):

但总的来说牛顿法由于需要求解Hessian 矩阵,所以计算代价过大,对问题规模较大的优化问题力不从心。
4.4.3 拟牛顿法(Quasi-Newton Method)
为解决Hessian 矩阵计算代价的问题,想到通过一阶信息去估计它的办法,于是涌现出一类方法,其中最有代表性的是DFP和BFGS(L-BFGS),其原理如下:
\[ \begin{array}{l} \text{We set $f(x_k)=f_k$ and $\nabla f(x_k)$=$\nabla f_k$}\\ \because \nabla f_{k+1}\approx\nabla f_{k}+\nabla^2 f_{k}(x_{k+1}-x_k)\\ \therefore \nabla^2 f_{k}(x_{k+1}-x_k)\approx\nabla f_{k+1}-\nabla f_{k}\\ \text{our task is to approximate hessian matrix $\nabla^2 f_{k}$}\\ \textbf{set } s_k=x_{k+1}-x_k,y_k=\nabla f_{k+1}-\nabla f_k\\ \text{and the low-rank approximating of hessian matrix is $B_{k+1}$ then}\\ 1.B_{k+1}s_k=y_k \quad \quad \\ 2.\text{$B_{k+1}$must be symmetric.}\\ 3.\text{We hope the new matrix can be stable and does not change wildly from iteration to iteration.}\\ \text{so we have a optimization problem:}\\ * \textbf{DFP}.\\ min ||B-B_{k}||_W\\ s.t.\;B=B^T\\ \quad \quad Bs_k=y_k\\ where\; ||B-B_{k}||_W=||W^{1/2}(B-B_k)W^{1/2}||\\ \text{W is any matrix satisfying } Wy_k=s_k\\ \text{The solution of this problem is:}\\ B_{k+1}=(I-(y_k^Ts_k)^{-1}y_ks_k^T)B_k(I-(y_k^Ts_k)^{-1}s_ky_k^T)+(y_k^Ts_k)^{-1}y_ky_k^T\\ \text{Note that if the initial Hessian approximation B_0 is positive definite then B_k will be positive definite}\\ \text{This algorithm is called DFP, named after Davidson, who discovered it in 1959, and Fletcher and Powell.}\\ \\ * \textbf{BFGS}.\\ \text{If we directly approximate Hessian's inverse $H_k=B_k^{-1}$ then we have a optimization problem:}\\ min ||H-H_{k}||_W\\ s.t.\;H=H^T\\ \quad \quad Hy_k=s_k\\ where\; ||H-H_{k}||_W=||W^{1/2}(H-H_k)W^{1/2}||\\ \text{W is any matrix satisfying } Ws_k=y_k\\ \text{The solution of this problem is:}\\ H_{k+1}=(I-(y_k^Ts_k)^{-1}s_ky_k^T)H_k(I-(y_k^Ts_k)^{-1}y_ky_s^T)+(y_k^Ts_k)^{-1}s_ks_k^T\\ \end{array} \]
一些有用的资料:
- 最优化相关书籍首推:《Numerical Optimization 2nd ed (Jorge Nocedal, Stephen J.Wright)》
- vw源码:vowpal_wabbit
- John Langford的博客
4.5 OWL-QN算法
4.5.1 BFGS算法回顾
算法思想如下:
Step1: 取初始点\(x^{(0)}\) ,初始正定矩阵\(H_0\),允许误差\(\epsilon>0\),令\(k=0\)
Step2: 计算: \[p^{(k)}=-H_k \nabla f(x^{(k)})\]
Step3: 计算\(\alpha_k>0\),使得: \[f(x^{(k)}+\alpha_kp^{(k)})=\min\limits_{\alpha \geq 0} f(x^{(k)}+\alpha p^{(k)})\]
Step4: 令: \[x^{(k+1)}=x^{(k)}+\alpha_k p^{(k)}\]
Step5: 如果\[||\nabla f(x^{(k+1)})|| \leq \epsilon\],则取\(x^{(k+1)}\)为近似最优解;否则转下一步
Step6: 计算:
\[s_k=x^{(k+1)}-x^{(k)}\]
\[y_k=\nabla f(x^{(k+1)})-\nabla f(x^{(k)})\]
\[H_{k+1}=H_k+\frac{1}{s_k^Ty_k}(1+\frac{y_k^TH_ky_k}{s_k^Ty_k})s_ks_k^T-\frac{1}{s_k^Ty_k}(s_ky_k^TH_k+H_ky_ks_k)\]
令\(k=k+1\),转Step2.
优点:
1、不用直接计算Hessian矩阵;
2、通过迭代的方式用一个近似矩阵代替Hessian矩阵的逆矩阵。
缺点:
1、矩阵存储量为\(n^2\),因此维度很大时内存不可接受;
2、矩阵非稀疏会导致训练速度慢。
4.5.2 L-BFGS算法
针对BFGS的缺点,主要在于如何合理的估计出一个Hessian矩阵的逆矩阵,L-BFGS的基本思想是只保存最近的m次迭代信息,从而大大降低数据存储空间。对照BFGS,我重新整理一下用到的公式:
\[\rho_k=\frac{1}{y_{k}^T s_k} s_k=x_k-x_{k-1} y_k\\ =\nabla{f(x_k)}-\nabla{f(x_{k-1})} V_k\\ =I-\rho_{k}y_{k}s_{k}^T \]
于是估计的Hessian矩阵逆矩阵如下:
\[ H_k=(I-\rho_{k-1}s_{k-1}y_{k-1}^T)H_{k-1}(I-\rho_{k-1}y_{k-1}s_{k-1}^T)+s_{k-1}\rho_{k-1}s_{k-1}^T \\ =V_{k-1}^TH_{k-1}V_{k-1}+ s_{k-1}\rho_{k-1}s_{k-1}^T \]
把 \[ H_{k-1}=V_{k-2}^TH_{k-2}V_{k-2}+ s_{k-2}\rho_{k-2}s_{k-2}^T\]
带入上式,得:
\[H_k=V_{k-1}^TV_{k-2}^TH_{k-2}V_{k-2}V_{k-1}+ V_{k-1}^Ts_{k-2}\rho_{k-2}s_{k-2}^T V_{k-1}+s_{k-1}\rho_{k-1}s_{k-1}^T \]
假设当前迭代为\(k\),只保存最近的\(m\)次迭代信息,(即:从\(k-m~k-1\)),依次带入\(H\),得到:
公式1:
\[H_k=(V_{k-1}^TV_{k-2}^T\ldots V_{k-m}^T) H_k^{0}(V_{k-m}\ldots V_{k-2}V_{k-1}) + (V_{k-1}^TV_{k-2}^T\ldots V_{k-m+1}^T) S_{k-m}\rho_{k-m}S_{k-m}^T (V_{k-m}\ldots V_{k-2}V_{k-1})\\ + (V_{k-1}^TV_{k-2}^T\ldots V_{k-m+2}^T) S_{k-m+1}\rho_{k-m+1}S_{k-m+1}^T (V_{k-m+1}\ldots V_{k-2}V_{k-1})\\ +\ldots +V_{k-1}^T s_{k-2}\rho_{k-2} s_{k-2}^TV_{k-1} +s_{k-1}\rho_{k-1}s_{k-1}^T \]
算法第二步表明了上面推导的最终目的:找到第k次迭代的可行方向,满足:
\[ p_k=-H_k\nabla f(x_k)\]
为了求可行方向\(p\),有下面的:
two-loop recursion算法:
\[ \begin{align*} &q=\nabla f(x_k) \\ &for (i=1 \ldots m) \quad do \\ &\quad \alpha_i=\rho_{k-i}s_{k-i}^Tq\\ &\quad q=q-\alpha_iy_{k-i}\\ &end \quad for\\ &r=H_k^{0}q \\ &for (i=m \ldots 1) \quad do\\ &\quad \beta=\rho_{k-i}y_{k-i}^Tr \\ &\quad r=r+s_{k-i}(\alpha_i-\beta)\\ &end \quad for\\ &return \quad r \end{align*} \]
该算法的正确性推导:
1、令: $ q_0=f(x_k)$ ,递归带入\(q\):
\[ \begin{align*} q_i&=q_{i-1}-\rho_{k-i}y_{k-i}s_{ki}^Tq_{i-1}\\ &=(I-\rho_{k-i}y_{k-i}s_{k-i}^T)q_{i-1} \\ &=V_{k-i}q_{i-1}\\ &=V_{k-i}V_{k-i+1}q_{i-2}\\ &=\ldots \\ & =V_{k-i}V_{k-i+1} \ldots V_{k-1} q_0\\ &=V_{k-i}V_{k-i+1} \ldots V_{k-1} \nabla f(x_k) \end{align*} \]
相应的:
\[ \begin{align*} \alpha_i&=\rho_{k-i}s_{k-i}^Tq_{i-1}\\ &=\rho_{k-i}s_{k-i}^T V_{k-i+1}V_{k-i+2} \ldots V_{k-1} \nabla f(x_k) \end{align*} \]
2、令:\(r_{m+1}=H_{k-m}q=H_{k-m}V_{k-i}V_{k-i+1} \ldots V_{k-1} \nabla f(x_k)\)
\[ \begin{align*} r_i&=r_{i+1}+s_{k-i}(\alpha_i-\beta)\\ &=r_{i+1}+s_{k-i}(\alpha_i-\rho_{k-i}y_{k-i}^Tr_{i+1}) \\ &=s_{k-i}\alpha_i+(I-s_{k-i}\rho_{k-i}y_{k-i}^T)r_{i+1}\\ &=s_{k-i}\alpha_{i}+V_{k-i}^Tr_{i+1} \end{align*} \]
于是:
\[ \begin{align*} r_1&=s_{k-1}\alpha_1+V_{k-1}^Tr_2 =s_{k-1}\rho_{k-1}s_{k-1}^T \nabla f(x_k)+V_{k-1}^Tr_2\\ &=s_{k-1}\rho_{k-1}s_{k-1}^T \nabla f(x_k)+V_{k-1}^T(s_{k-2}\alpha_2+V_{k-2}^Tr_3)\\ &=s_{k-1}\rho_{k-1}s_{k-1}^T \nabla f(x_k)+V_{k-1}^Ts_{k-2}\rho_{k-2}s_{k-2}^TV_{k-1}\nabla f(x_k)+V_{k-1}^T V_{k-2}^T r_3\\ &=\ldots \\ &=s_{k-1}\rho_{k-1}s_{k-1}^T \nabla f(x_k)\\ &+V_{k-1}^T s_{k-2}\rho_{k-2} s_{k-2}^TV_{k-1} \nabla f(x_k)\\ &+\ldots\\ &+ (V_{k-1}^TV_{k-2}^T\ldots V_{k-m+2}^T) S_{k-m+1}\rho_{k-m+1}S_{k-m+1}^T (V_{k-m+1}\ldots V_{k-2}V_{k-1}) \nabla f(x_k)\\ &+ (V_{k-1}^TV_{k-2}^T\ldots V_{k-m+1}^T) S_{k-m}\rho_{k-m}S_{k-m}^T (V_{k-m}\ldots V_{k-2}V_{k-1}) \nabla f(x_k)\\ &+(V_{k-1}^TV_{k-2}^T\ldots V_{k-m}^T) H_{k-m}(V_{k-m}\ldots V_{k-2}V_{k-1}) \nabla f(x_k) \end{align*} \]
这个two-loop recursion算法的结果和**公式1*初始梯度**的形式完全一样,这么做的好处是:
1、只需要存储\(s_{k-i}、y_{k-i} (i=1~m)\);
2、计算可行方向的时间复杂度从\(O(n*n)\)降低到了\(O(n*m)\),当\(m\)远小于\(n\)时为线性复杂度。
总结L-BFGS算法的步骤如下:
Step1:选初始点\(x_0\),允许误差\(\epsilon >0\),存储最近迭代次数\(m\)(一般取6);
Step2:\(k=0, \quad \ H_0=I , \quad r=\nabla f(x_{0})\);
Step3:如果 \(||\nabla f(x_{k+1})||\leq \epsilon\) 则返回最优解\(x_{k+1}\),否则转Step4;
Step4:计算本次迭代的可行方向:\(p_k=-r _k\);
Step5: 计算步长\(\alpha_k>0\),对下面式子进行一维搜索:
\[f(x_k+\alpha_kp_k)=\min\limits_{\alpha \geq 0} \quad f(x_k+\alpha p_k)\]
Step6:更新权重\(x\):
\[ x_{k+1}=x_k+\alpha_kp_k\]
Step7: 如果 $ k > m$ 只保留最近m次的向量对,需删除(\(s_{k-m},y_{k-m}\));
Step8:计算并保存: \[ \begin{align*} s_k&=x_{k+1}-x_k\\ y_k&=\nabla f(x_{k+1})-\nabla f(x_k) \end{align*} \]
Step9:用two-loop recursion算法求得: \[r_k=H_k\nabla f(x_k)\]
\(k=k+1\),转Step3。
需要注意的地方,每次迭代都需要一个\(H_{k-m}\) ,实践当中被证明比较有效的取法为:
\[ \begin{align*} H_k^0&=\gamma_k I\\ \gamma_k&=\frac{s_{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}} \end{align*} \]
4.5.3 OWL-QN算法原理
1、问题描述
对于类似于Logistic Regression这样的Log-Linear模型,一般可以归结为最小化下面这个问题:
\[ J(x)=l(x)+r(x) \] 其中,第一项为loss function,用来衡量当训练出现偏差时的损失,可以是任意可微凸函数(如果是非凸函数该算法只保证找到局部最优解),后者为regularization term,用来对模型空间进行限制,从而得到一个更“简单”的模型。 根据对模型参数所服从的概率分布的假设的不同,regularization term一般有:L2-norm(模型参数服从Gaussian分布);L1-norm(模型参数服从Laplace分布);以及其他分布或组合形式。
L2-norm的形式类似于:
\[ J(x)=l(x)+C\sum\limits_i{x_i^2} \] L1-norm的形式类似于:
\[ J(x)=l(x)+C\sum\limits_i{|x_i|} \]
L1-norm和L2-norm之间的一个最大区别在于前者可以产生稀疏解,这使它同时具有了特征选择的能力,此外,稀疏的特征权重更具有解释意义。
对于损失函数的选取就不在赘述,看两幅图: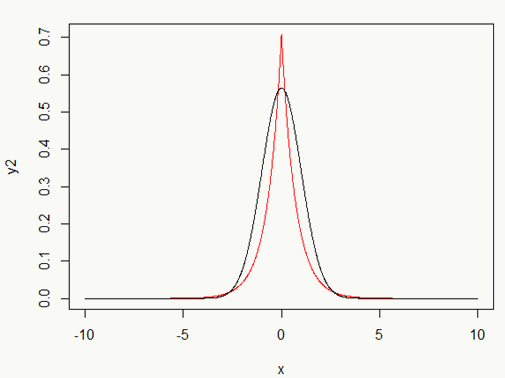 图1 - 红色为Laplace Prior,黑色为Gaussian Prior
图1 - 红色为Laplace Prior,黑色为Gaussian Prior 图2 直观解释稀疏性的产生
图2 直观解释稀疏性的产生对LR模型来说损失函数选取凸函数,那么L2-norm的形式也是的凸函数,根据最优化理论,最优解满足KKT条件,即有:\(\nabla J(x^*)=0\) ,但是L1-norm的regularization term显然不可微,怎么办呢?
2、Orthant-Wise Limited-memory Quasi-Newton
OWL-QN主要是针对L1-norm不可微提出的,它是基于这样一个事实:任意给定一个维度象限,L1-norm 都是可微的,因为此时它是一个线性函数: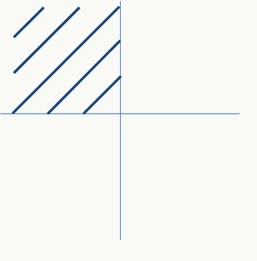 图3 任意给定一个象限后的L1-norm
图3 任意给定一个象限后的L1-normOWL-QN中使用了次梯度决定搜索方向,凸函数不一定是光滑而处处可导的,但是它又符合类似梯度下降的性质,在多元函数中把这种梯度叫做次梯度,见维基百科http://en.wikipedia.org/wiki/Subderivative
举个例子: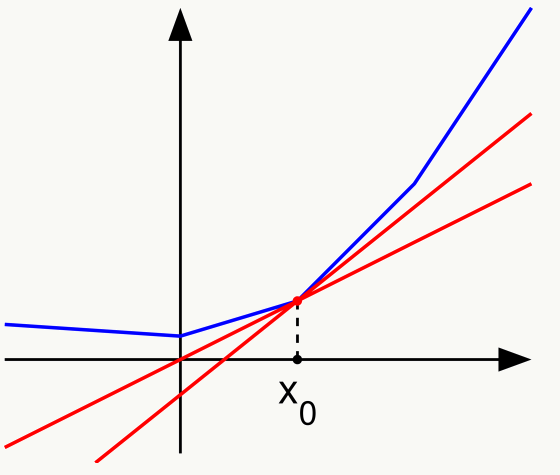 图4 次导数
图4 次导数对于定义域中的任何\(x_0\),我们总可以作出一条直线,它通过点\((x_0, f(x_0))\),并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数,推广到多元函数就叫做次梯度。
次导数及次微分: 凸函数\(f:I→R\)在点\(x_0\)的次导数,是实数c使得:
\[ f(x)-f(x_0)\ge c(x-x_0) \] 对于所有I内的x。可以证明,在点x0的次导数的集合是一个非空闭区间[a, b],其中a和b是单侧极限
\[ a=\lim_{x\to x_0^-}\frac{f(x)-f(x_0)}{x-x_0}\\ b=\lim_{x\to x_0^+}\frac{f(x)-f(x_0)}{x-x_0} \]
它们一定存在,且满足\(a ≤ b\)。所有次导数的集合\([a, b]\)称为函数\(f\)在\(x_0\)的次微分。
OWL-QN和传统L-BFGS的不同之处在于:
- 利用次梯度的概念推广了梯度 定义了一个符合上述原则的虚梯度,求一维搜索的可行方向时用虚梯度来代替L-BFGS中的梯度: \[ \begin{align*} \Diamond_i f(x) &=\left\{ \begin{array}{**lr**} \partial_i^{-}f(x) & if &\partial_i^{-}f(x)>0 \\ \partial_i^{+}f(x)& if &\partial_i^{+}f(x)<0\\ 0 & &otherwise \end{array} \right.\\ \partial_i^{\pm}f(x)&=\frac{\partial}{\partial x_i}l(x)+\left\{ \begin{array}{**lr**} C\sigma (x_i) & if &x_i\neq 0\\ \pm C& if & x_i=0 \end{array} \right.\\ \partial_i^{-}f(x) &\leq \partial_i^{+}f(x) \end{align*} \] 怎么理解这个虚梯度呢?见下图: 对于非光滑凸函数,那么有这么几种情况:
![]() 图5 \(\partial_i^-f(x)>0\)
图5 \(\partial_i^-f(x)>0\)![]() 图6 \(\partial_i^+f(x)<0\)
图6 \(\partial_i^+f(x)<0\)![]() 图7 otherwise
图7 otherwise - 一维搜索要求不跨越象限 要求更新前权重与更新后权重同方向:
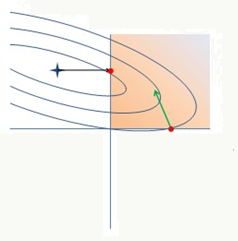 图8 OWL-QN的一次迭代
图8 OWL-QN的一次迭代总结OWL-QN的一次迭代过程:
Find vector of steepest descent
Choose sectant
Find L-BFGS quadratic approximation
Jump to minimum
Project back onto sectant
Update Hessian approximation using gradient of loss alone
最后OWL-QN算法框架如下:

与L-BFGS相比,第一步用虚梯度代替梯度,第二、三步要求一维搜索不跨象限,也就是迭代前的点与迭代后的点处于同一象限,第四步要求估计Hessian矩阵时依然使用loss function的梯度(因为L1-norm的存在与否不影响Hessian矩阵的估计)。
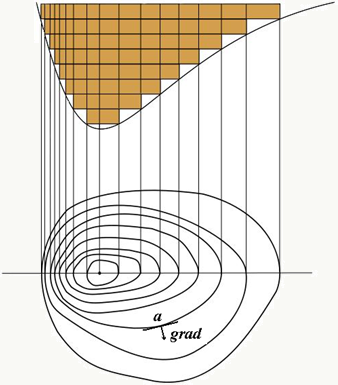
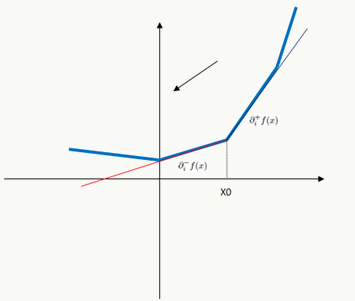 图5
图5 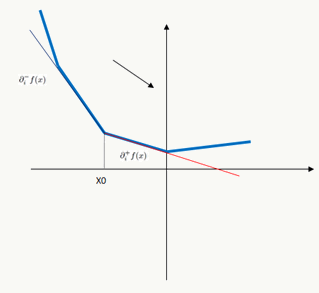 图6
图6 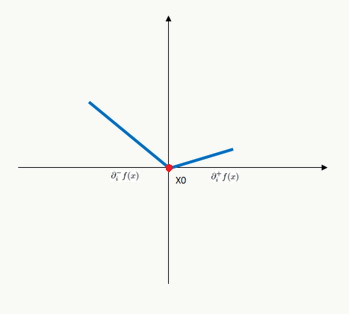 图7 otherwise
图7 otherwise