本章介绍关于机器学习的一些基本概念，包括生成式模型和判别式模型、非参学习等。
1. 一些基本概念
1.1 生成式模型与判别式模型
从概率分布的角度看待模型。 给个例子感觉一下: 如果我想知道一个人A说的是哪个国家的语言，我应该怎么办呢?
生成式模型
我把每个国家的语言都学一遍，这样我就能很容易知道A说的是哪国语言，并且C、D说的是哪国的我也可以知道，进一步我还能自己讲不同国家语言。
判别式模型
我只需要学习语言之间的差别是什么，学到了这个界限自然就能区分不同语言，我能说出不同语言的区别，但我可能不会讲。
如果我有输入数据\(x\)，并且想通过标注\(y\)去区分不同数据属于哪一类，生成式模型是在学习样本和标注的联合概率分布 \(p(x,y)\) 而判别式模型是在学习条件概率 \(p(y|x)\)。 生成式模型\(p(x,y)\)可以通过贝叶斯公式转化为\(p(y|x)=\frac{p(x,y)}{p(x)}\)，并用于分类，而联合概率分布\(p(x,y)\)也可用于其他目的，比如用来生成样本对\((x,y)\)。
判别式模型的主要任务是找到一个或一系列超平面，利用它(们)划分给定样本\(x\)到给定分类\(y\)，这也能直白的体现出“判别”模型这个名称。
最后给一个很简单的例子说明一下： 假如我有以下独立同分布的若干样本\((x,y)\)，其中\(x\)为特征，\(y\in\{0,1\}\)为标注,\((x,y)\in\{(2,-1),(2,-1),(3,-1),(3,1),(3,1)\}\)，则：
\(p(x,y)\)
\(p(x,y)\) \(y=-1\) \(y=1\) \(x=2\) \(2/5\) \(0\) \(x=3\) \(1/5\) \(2/5\) \(p(y|x)\)
\(p(y|x)\) \(y=-1\) \(y=1\) \(x=2\) \(1\) \(0\) \(x=3\) \(1/3\) \(2/3\)
一些理论可看：On Discriminative vs Generative classifiers: A comparison of logistic regression and naive Bayes。
常见生成式模型
Naive Bayes
Gaussians
Mixtures of Gaussians
Mixtures of Experts
Mixtures of Multinomials
HMM
Markov random fields
Sigmoidal belief networks
Bayesian networks
常见判别式模型
Linear regression
Logistic regression
SVM
Perceptron
Traditional Neural networks
Nearest neighbor
Conditional random fields
1.2 参数学习与非参学习
从参数与样本的关系角度看待模型。
1.2.1 参数学习
参数学习的特点是：
选择某种形式的函数并通过机器学习用一系列固定个数的参数尽可能表征这些数据的某种模式；
不管数据量有多大，函数参数的个数是固定的，即参数个数不随着样本量的增大而增加，从关系上说它们相互独立；
往往对数据有较强的假设，如分布的假设，空间的假设等。
常用参数学习的模型有：
Logistic Regression
Linear Regression
Polynomial regression
Linear Discriminant Analysis
Perceptron
Naive Bayes
Simple Neural Networks
使用线性核的SVM
Mixture models
K-means
Hidden Markov models
Factor analysis / pPCA / PMF
1.2.2 非参学习
注意不要被名字误导，非参不等于无参。
数据决定了函数形式，函数参数个数不固定；
随着数据量的增加，参数个数一般也会随之增长；
对数据本身做较少的先验假设。
一些常用的非参学习模型：
k-Nearest Neighbors
Decision Trees like CART and C4.5
使用非线性核的SVM
Gradient Boosted Decision Trees
Gaussian processes for regression
Dirichlet process mixtures
infinite HMMs
infinite latent factor models
进一步知识可以看：Parametric vs Nonparametric Models。
1.3 监督学习、非监督学习与强化学习
1.3.1 监督学习
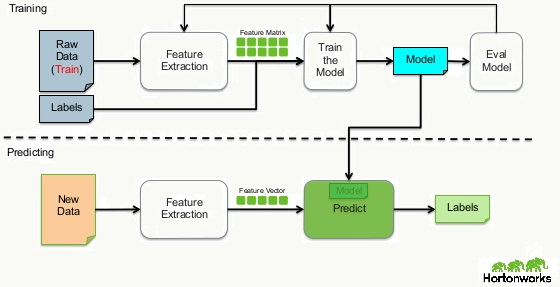
对于每一个样本都会提供一个明确的学习目标（标注），有自变量也有因变量，学习机接收样本进行学习并通过对该样本预测后的结果和事先给定的目标比较后修正学习过程，这里的每一个样本都是标注好的，所以好处是歧义较低，坏处是万一有一定量样本标错了或者没标会对最终应用效果影响较大。通常监督学习过程如下：
picture from here1.3.2 非监督学习
对于每个样本不提供明确的学习目标（标注），有自变量但无因变量，学习机接收样本后会按事先指定的必要参数，依据某种相似度衡量方式自动学习样本内部的分布模式，好处是没有过多先验假设，能够体现数据内在模式并应用，坏处是有“盲目”性，并会混在噪声数据。比如：常用LDA做主题聚类，但如果使用场景不是降维而是想得到可输出的主题词，基本上没有人肉的干预无法直接使用（虽然整体上看感觉可能不错）。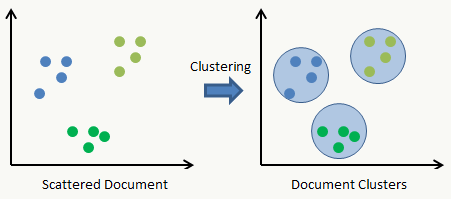
picture from here1.3.3 强化学习
我认为强化学习是最接近人类学习过程的，很多情况下我们无法直接表达什么是正确的什么是错误的（比如：我正在爬山，迈了一大步，又迈了一小步，那么没法儿说我迈了大步正确还是错误），但是可以通过惩罚不好的结果或者奖励好的结果来强化学习的效果（我迈了个大步，导致没有站稳，那么对迈大步做惩罚，然后接下来我会迈小一点）。所以强化学习是一个序列的决策过程，学习机的学习目标是通过在给定状态下选择某种动作，寻找合适动作的策略序列使得它可以获得某种最优结果的过程。 强化学习的几个要素，体现其序列、交互性：
- 环境(environment)：强化学习所处的上下文；
- 学习器(agent)：与环境的交互并学习的对象，具有主动性；
- 动作(action)：处于环境下的可行动作集合；
- 反馈(feedback)：对动作的回报或惩罚；
- 策略(policy)：学习到的策略链。
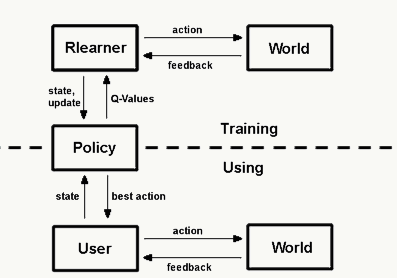picture from here
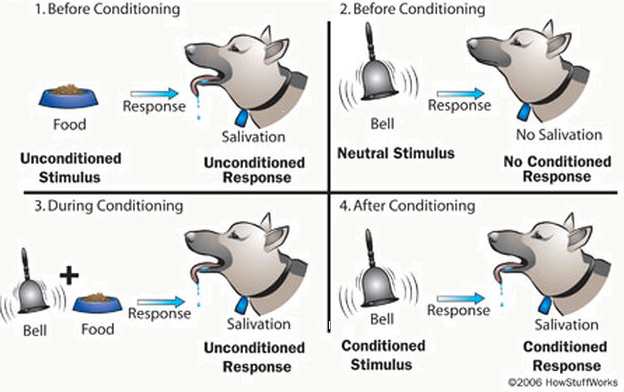picture from here强化学习的有趣应用例如：