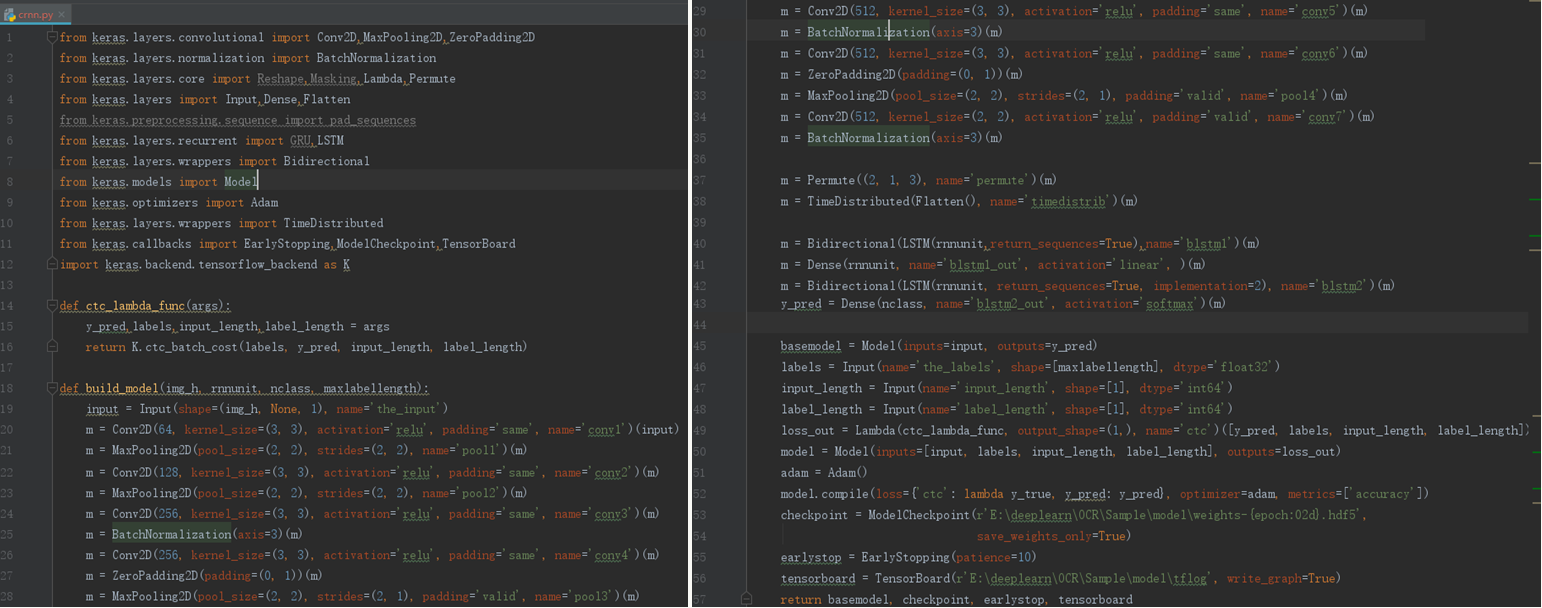
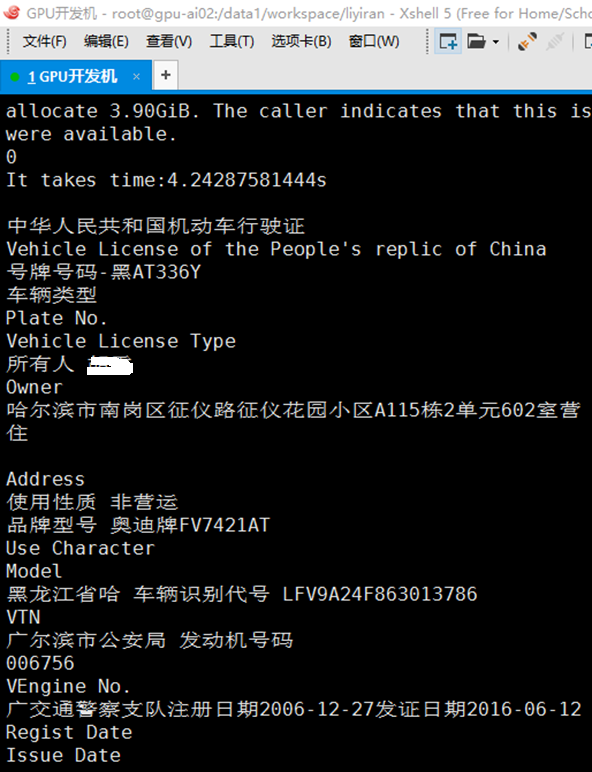
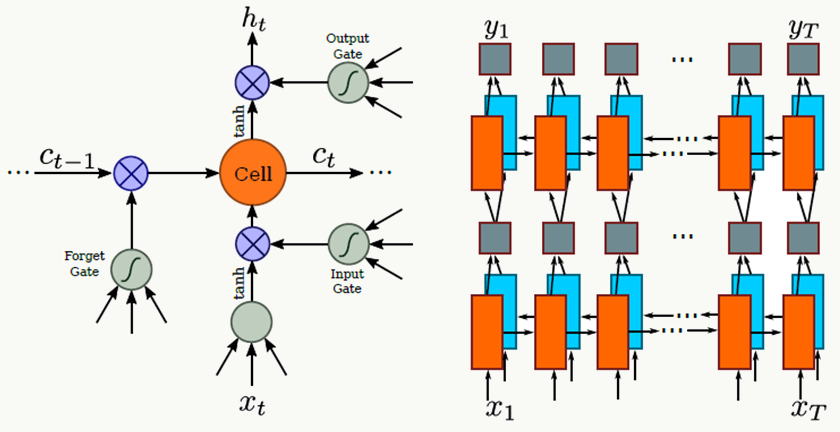
本章对于机器学习在OCR中的应用过程及早期经典模型做了介绍,抛砖引玉。
本章对于机器学习在OCR中的应用过程及早期经典模型做了介绍,抛砖引玉。
11. OCR
11.1 背景知识
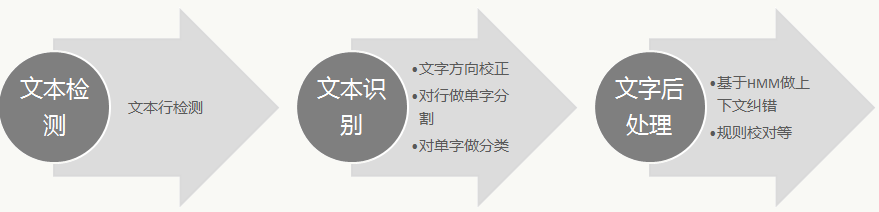
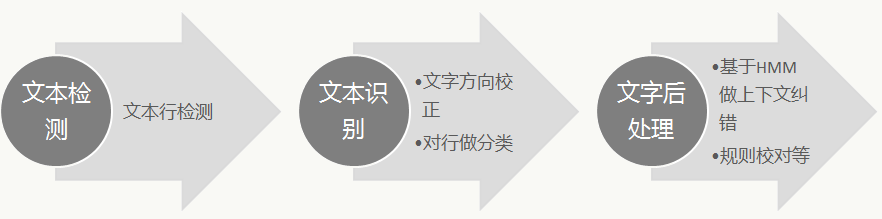
OCR是将各种带有文字的图像数据中的文本信息定位并识别成可编辑文本的技术。其核心技术包括:文本位置检测、文本内容识别等,OCR的一般过程是:

图片预处理阶段会对光照、清晰度、角度等方面做算法处理,让进入后续流程的图片尽可能质量好;
针对类似发票、报纸等有固定版面的业务场景,可以对位置、内容做处理,提高后续识别的准确率;
文本行检测,用来定位图像中的文本行的位置、大小,是OCR的一个难点;
文本识别,用来对定位好的文本行做文字分类,这里有两类方法:
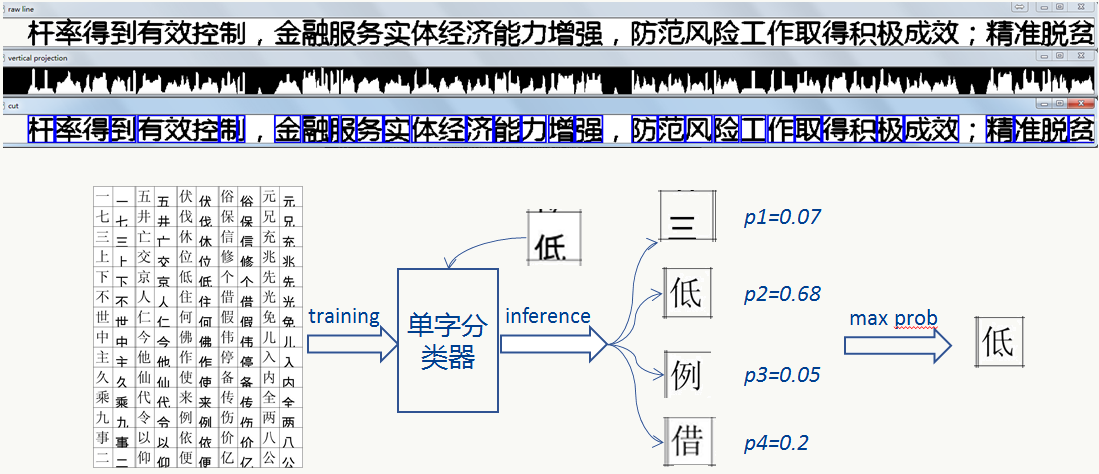
- 先对单字做切割然后再做单字分类,除去公共流程如预处理、版面分析等,基本流程为:
![]()
![]()
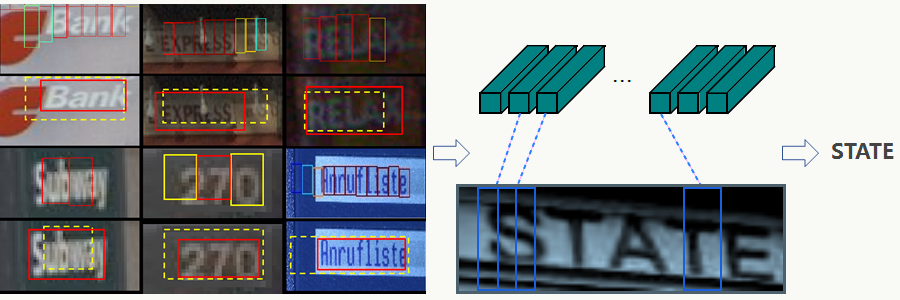
- 直接对一行文本做分类,免去了单字分割操作而直接对一行文本做识别,基本流程为:
![]()
![]()
- 先对单字做切割然后再做单字分类,除去公共流程如预处理、版面分析等,基本流程为:
文字后处理,由于文本具有上下文语义关系,可以利用NLP技术对识别结果做修正,进一步提高识别准确率。
11.2 数据预处理
11.2.1 图像滤波
滤波本质上是在尽量保持原有图像细节(不破坏诸如边缘、轮廓等信息)的条件下对噪声尽可能抑制(提高图像视觉效果)的操作,完成这个操作,潜在的同时做了两件事:抽取了图像的某种特征和去除了某种噪声(类似的还有深度学习中的AutoEncoder架构),一般架构如下: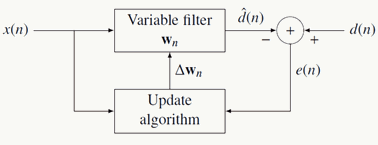
滤波是一个很复杂的课题,简单来说会有时空域滤波和频域滤波两大类,而转换时空与频率的工具就是(逆)傅里叶变换(Transformée de Fourier):任何周期函数都可以表达为不同频率的正弦和或余弦和的形式,即傅里叶级数,其本质是不同空间的换基分解操作。
1、时空滤波
基本思路是,用一个滤波器(又叫一个模版、窗口)在待处理图像上逐点移动,在每一个点做某种线性或者非线性函数操作(深度学习中的卷积操作是一种典型的滤波)。
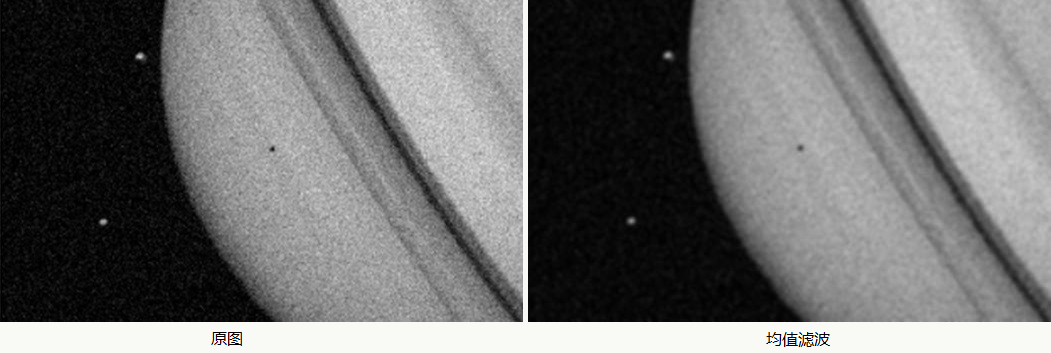
均值滤波
对当前像素点用滤波器领域内的像素点值求加权平均后代替该像素点值得到一幅减噪的图像,会对图像产生模糊作用:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27import numpy as np
import PIL.Image
import scipy.misc as ms
import scipy.signal
def mean_2d(r, n=5):
if n < 1:
print("[ERROR] Filter's size must >= 1.")
return None
win = np.ones((n, n)) / n ** 2 # filter每个元素系数值为1/(n*n)
s = scipy.signal.convolve2d(r, win, mode='same', boundary='symm') # 做same padding
return s.astype(np.uint8)
def justdoit(r):
sp = []
for dim in range(r.shape[2]):
rd = r[:, :, dim]
sd = mean_2d(rd)
sp.append(sd)
s = np.dstack(sp)
return s
img = PIL.Image.open('/data1/liyiran/idcard-gen/idcard-gen/angle/star.jpg')
img_matrix = ms.fromimage(img)
im_conv_mat = justdoit(img_matrix)
im_conv = PIL.Image.fromarray(im_conv_mat)
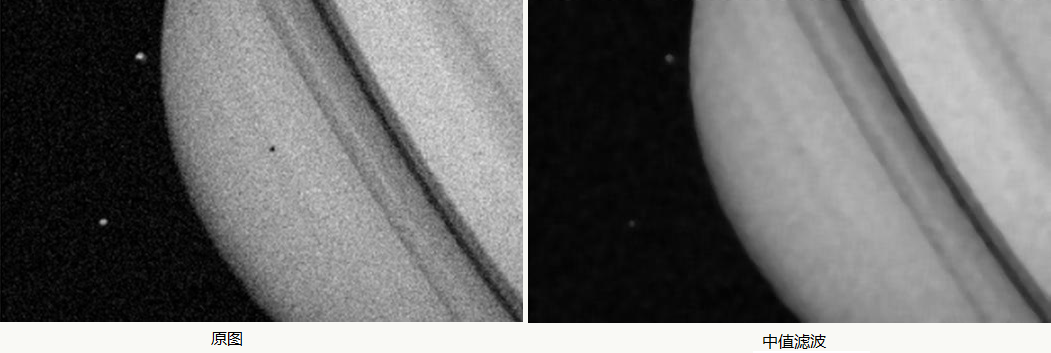
im_conv.save('mean.jpg')中值滤波/最大值滤波/最小值滤波
对当前像素点用滤波器领域内的像素点值的中值/最大值/最小值代替该像素点值得到一幅减噪的图像,对图像脉冲噪声很有作用:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23import numpy as np
import PIL.Image
import scipy.misc as ms
import scipy.signal
def middle_2d(r, n=10):
s = scipy.ndimage.median_filter(r, (n, n))
return s.astype(np.uint8)
def justdoit(r):
sp = []
for dim in range(r.shape[2]):
rd = r[:, :, dim]
sd = middle_2d(rd)
sp.append(sd)
s = np.dstack(sp)
return s
img = PIL.Image.open('/data1/liyiran/idcard-gen/idcard-gen/angle/star.jpg')
img_matrix = ms.fromimage(img)
im_conv_mat = justdoit(img_matrix)
im_conv = PIL.Image.fromarray(im_conv_mat)
im_conv.save('middle.jpg')高斯滤波
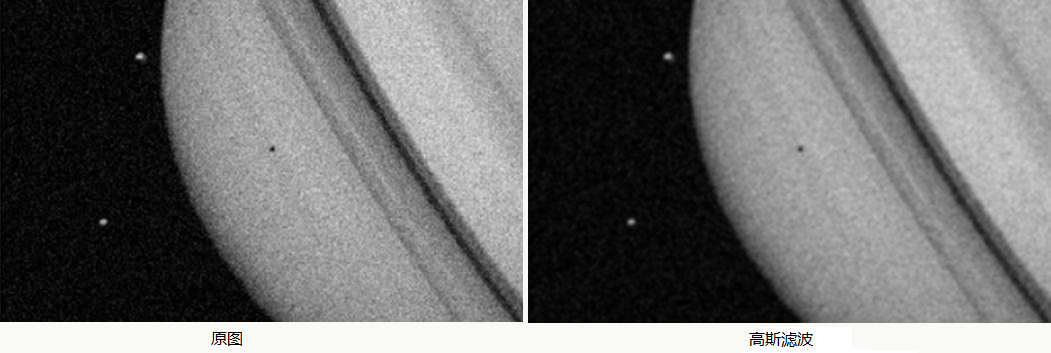
是一种线性平滑的低通滤波,如果噪声服从高斯分布则效果会很好,它是对图片的每一个像素点的值由滤波器邻域内的其他像素值和该像素值本身加权平均求和后得到,权重的生成服从高斯分布:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34import numpy as np
import PIL.Image
import scipy.misc as ms
import scipy.signal
import math
def get_win(radius, sigma):
window = np.zeros((radius * 2 + 1, radius * 2 + 1))
cdf = 1 / (2 * math.pi * sigma ** 2) * math.exp((-radius**2) / (2 * sigma ** 2))
for i in range(-radius, radius + 1):
for j in range(-radius, radius + 1):
r = (i ** 2 + j ** 2) ** 0.5
window[i + radius][j + radius] = cdf
return window / np.sum(window)
def gaussian(r):
window = get_win(3, 2.5)
s = scipy.signal.convolve2d(r, window, mode='same', boundary='symm')
return s.astype(np.uint8)
def justdoit(r):
sp = []
for dim in range(r.shape[2]):
rd = r[:, :, dim]
sd = gaussian(rd)
sp.append(sd)
s = np.dstack(sp)
return s
img = PIL.Image.open('/data1/liyiran/idcard-gen/idcard-gen/angle/star.jpg')
img_matrix = ms.fromimage(img)
im_conv_mat = justdoit(img_matrix)
im_conv = PIL.Image.fromarray(im_conv_mat)
im_conv.save('gaussian.jpg')锐化滤波
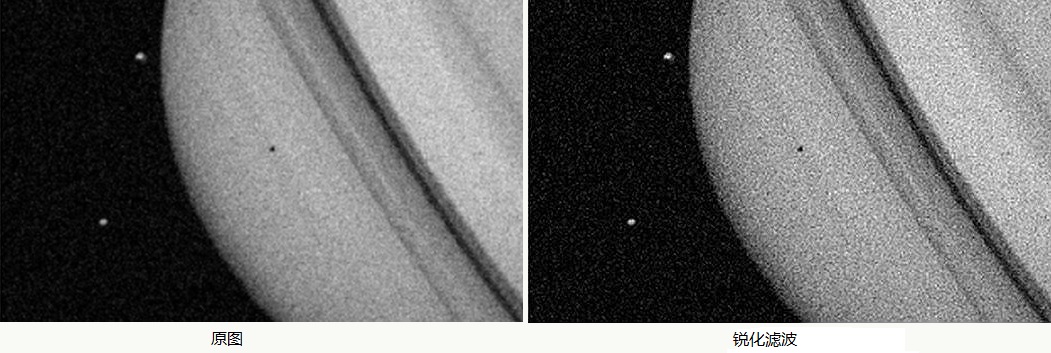
直接的视觉效果是使模糊的图像变得清晰,主要增强了图像的灰度跳变部分,与图像平滑类滤波器正好相反,原理上主要是对滤波器领域的梯度来实现,常用的有拉普拉斯算子、Robertt交叉梯度算子、Sobel梯度算子等,一个使用拉普拉斯算子的直观例子:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32import numpy as np
import PIL.Image
import scipy.misc as ms
import scipy.signal
def sharpen(r):
window = np.array([
[0, -1, 0],
[-1, 5, -1],
[0, -1, 0]
])
s = scipy.signal.convolve2d(r, window, mode='same', boundary='symm')
for i in range(s.shape[0]):
for j in range(s.shape[1]):
s[i][j] = min(max(0, s[i][j]), 255)
s = s.astype(np.uint8)
return s
def justdoit(r):
sp = []
for dim in range(r.shape[2]):
rd = r[:, :, dim]
sd = sharpen(rd)
sp.append(sd)
s = np.dstack(sp)
return s
img = PIL.Image.open('/data1/liyiran/idcard-gen/idcard-gen/angle/star.jpg')
img_matrix = ms.fromimage(img)
im_conv_mat = justdoit(img_matrix)
im_conv = PIL.Image.fromarray(im_conv_mat)
im_conv.save('sharpen.jpg')
2、频域滤波
分析一幅图像信号的频率特性,其中直流分量表示了图像的平均灰度;它的边缘、跳跃部分、噪声及图像细节代表了图像的高频分量;而背景区域和变化缓慢的部分代表了图像的低频分量。
低通滤波
在频域中利用滤波器函数衰减图像高频信息从而令低频信息畅通无阻的方法叫做低通滤波。在频域实现线性低通滤波器输出会被表达为为: \[ G(u,v)=H(u,v)F(u,v) \] 其中\(F(u,v)\)是输入,\(H(u,v)\)是线性低通滤波器,\(G(u,v)\)是输出,即:
![]()
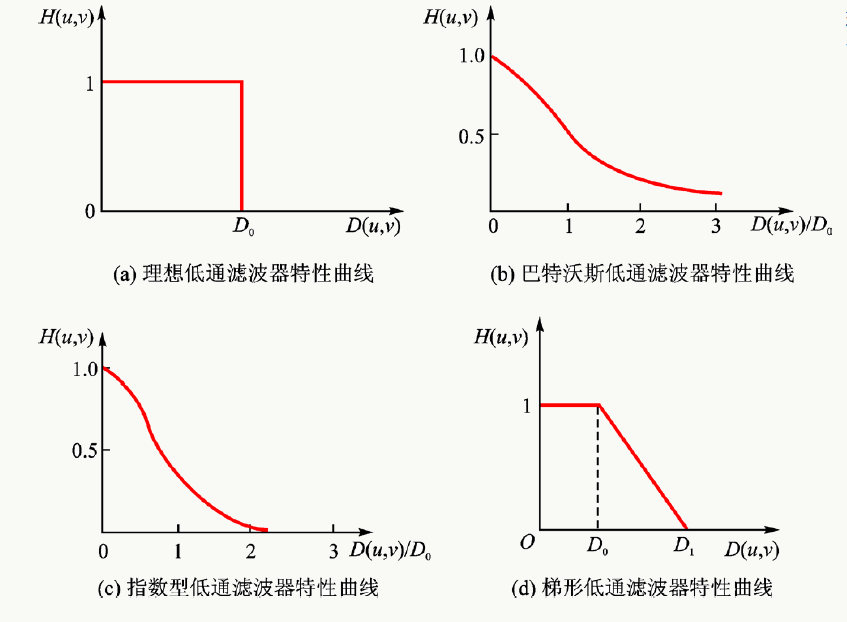
几种低通滤波传递函数的剖面图(有没有想到和0-1损失函数及其他损失函数?):
![]()
(1)、以理想低通滤波器为例,其传递函数为: \[ H(u,v)=\left\{ \begin{aligned} 1 & ,D(u,v)\leq D_0 \\ 0 & ,D(u,v)>D_0 \end{aligned} \right. \] 其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \] 直观上看,理想低通滤波器以\(D_0\)为半径的圆内的所有频率分量无损通过,而圆以外的所有频率分量全部衰减,小例子:
![]()
代码如下:
(2)、以Butterworth(巴特沃斯)低通滤波器为例,其传递函数为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25import cv2
import numpy as np
import math
def ideal_filter(img,d0=60):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
circle=np.zeros(img.shape,np.uint8)
for h in range(height):
for w in range(weight):
if math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2)) <= d0:
circle[h, w] = 255
fx = 1
else:
fx = 0
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return circle,id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
circle,id_img=ideal_filter(img)
cv2.imwrite("circle.png",circle)
cv2.imwrite("ideal.png",id_img)\[ H(u,v)=\frac{1}{1+(D(u,v)/D_0)^{2n}}\]
其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \] 直观上看,它的通带和阻带之间没有明显的不连续性,即通、阻带之间是平滑的,当\(n\)比较大时,Butterworth低通滤波器会退化为理想滤波器,小例子:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import cv2
import numpy as np
import math
def butterworth_filter(img,d0=60, n=2):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
for h in range(height):
for w in range(weight):
fx=1/(1+math.pow(math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2)) / d0, 2*n))
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
id_img=butterworth_filter(img)
cv2.imwrite("Butterworth.png",id_img)(3)、以高斯低通滤波器为例,其传递函数为:
\[ H(u,v)=e^{-(D(u,v)/D_0)^{2n}}\] 其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \] 直观上看,由于函数是平滑的,它的通带和阻带之间同样没有明显的不连续性,效果上比Butterworth模糊一点点,但没有振铃现象,小例子:
![]()
代码如下:
总的来数,低通滤波可以通过平滑处理使噪声减到不显眼的程度,但这种去噪美化处理是以牺牲清晰度为代价的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import cv2
import numpy as np
import math
def gaussian_filter(img,d0=60, n=2):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
for h in range(height):
for w in range(weight):
fx=math.exp(-1*math.pow(math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2)) / d0, 2*n))
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
id_img=gaussian_filter(img)
cv2.imwrite("Gaussian.png",id_img)高通滤波
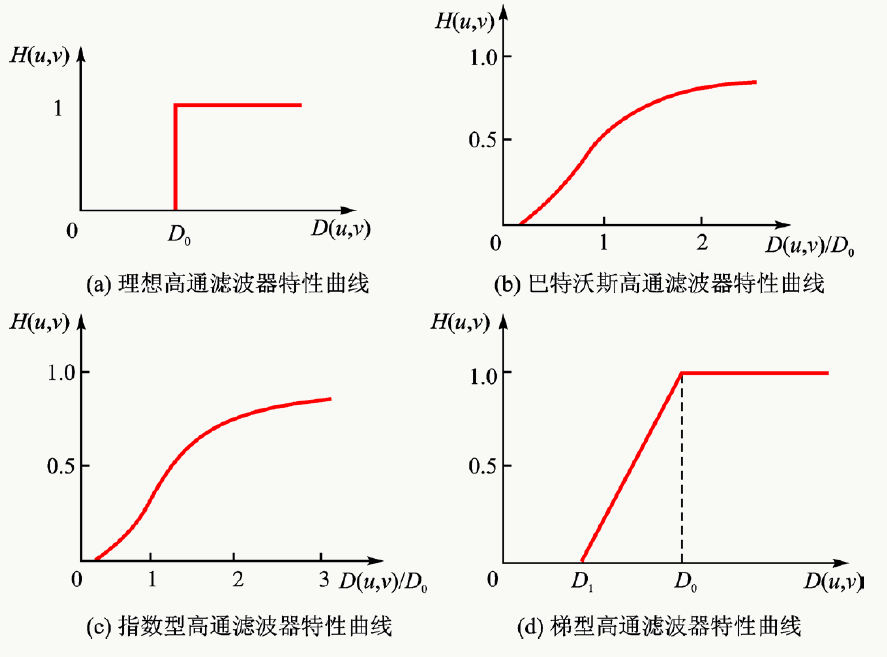
反过来我们看,由于图像的边缘、线条等细节与图像的高频分量相对应,通过衰减低频分量可以增强高频分量,从而使得图像细节看上去更“清晰”,这便是高通滤波。类比低通滤波,可以有以下几种高通滤波传递函数的剖面图:
![]()
(1)、以理想高通滤波器为例,其传递函数为:
\[ H(u,v)=\left\{ \begin{aligned} 0 & ,D(u,v)\leq D_0 \\ 1 & ,D(u,v)>D_0 \end{aligned} \right. \] 其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \]
直观上看,理想低通滤波器以\(D_0\)为半径的圆内的所有频率分量全部衰减,而圆以外的所有频率分量无损通过,小例子:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25import cv2
import numpy as np
import math
def ideal_filter(img,d0=60):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
circle=np.zeros(img.shape,np.uint8)
for h in range(height):
for w in range(weight):
if math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2)) <= d0:
circle[h, w] = 255
fx = 0
else:
fx = 1
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return circle,id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
circle,id_img=ideal_filter(img)
cv2.imwrite("circle.png",circle)
cv2.imwrite("ideal.png",id_img)(2)、以Butterworth(巴特沃斯)高通滤波器为例,其传递函数为:
\[ H(u,v)=\frac{1}{1+(D_0/D(u,v))^{2n}}\] 其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \] 小例子:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import cv2
import numpy as np
import math
def butterworth_filter(img,d0=60, n=2):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
for h in range(height):
for w in range(weight):
fx=1/(1+math.pow(d0 / (math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2)+0.1)), 2*n))
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
id_img=butterworth_filter(img)
cv2.imwrite("Butterworth.png",id_img)(3)、以高斯高通滤波器为例,其传递函数为:
\[H(u,v)=e^{-(D_0/D(u,v))^{2n}}\]
其中\(D_0\)为非负的截止频率,\(D(u,v)\)是从频域的远点到\((u,v)\)点的距离: \[ D(u,v)=\sqrt{(u-M/2)^2+(v-N/2)^2} \] 小例子:
![]()
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19import cv2
import numpy as np
import math
def gaussian_filter(img,d0=60, n=2):
fshift = np.fft.fftshift(np.fft.fft2(img))
org_fsh=fshift.copy()
height,weight=fshift.shape
for h in range(height):
for w in range(weight):
fx=math.exp(-1*math.pow( d0 / (math.sqrt(math.pow(h-height/2,2) + math.pow(w-weight/2,2))+0.1), 2*n))
org_fsh[h, w] = fx * fshift[h, w]
id_img=np.uint8(np.real(np.fft.ifft2(np.fft.ifftshift(org_fsh))))
return id_img
img=cv2.imread('e:/meizi.png',cv2.IMREAD_GRAYSCALE)
id_img=gaussian_filter(img)
cv2.imwrite("Gaussian.png",id_img)
11.2.2 去模糊、去水印
11.2.3 图片角度识别
图片角度识别做法类似构建一个分类和回归问题,套路之前已经讲过就不赘述了,最关键的还是训练数据,可以自己写代码生成各种角度的数据: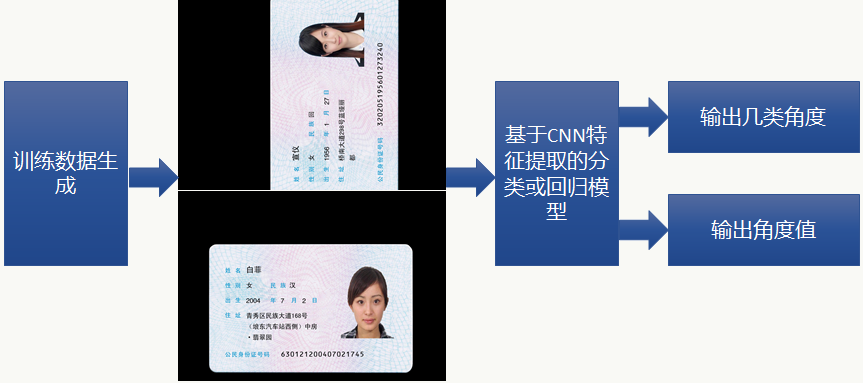
11.3 基于神经网络的文字OCR
11.3.1 行检测模型算法思路
文字的检测、物体的检测其实基本原理大同小异,本质上是在学习Bounding Box的边界以及启发式的做Bounding Box合并。以CTPN(https://arxiv.org/pdf/1609.03605.pdf)为例,借鉴Fast R-CNN做文本的行检测,即通过一个“框”把一整行文字的位置检测出来,进而送到后续识别模型,但由于检测文字行不像检测物体,一行字比较长且可能大小不一(尤其垂直方向上),对定位的精度要求更高,所以对于特征提取的基础神经网络需要对位置有较强的敏感性(检测模型要求对位置敏感,而识别模型恰好相反,所以要分场景应用模型)。
CTPN行检测整体思路: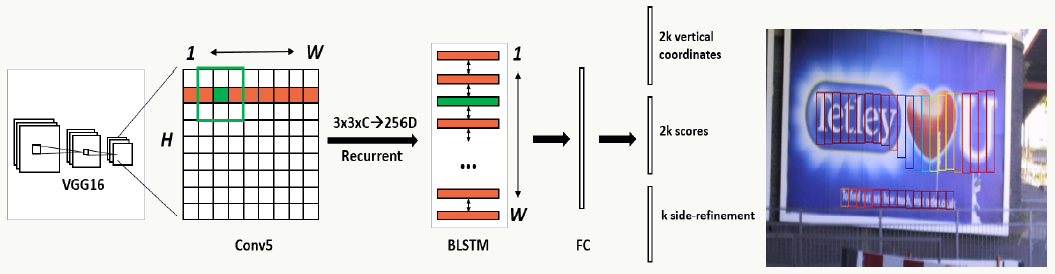
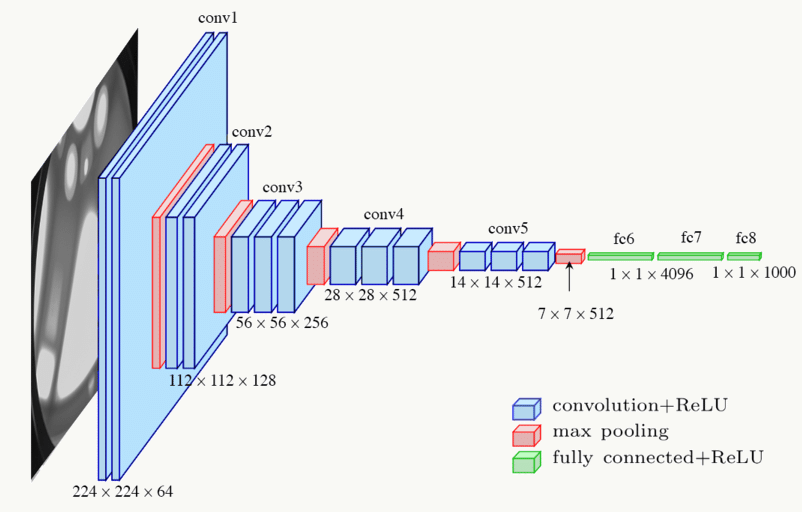
使用VGG16做特征提取
文中采用的基础网络为VGG16,这个模型前面有介绍,特点是:模型整体偏大,但是较好的保留了图片的局部位置信息:
![]()
使用滑动窗口生成一系列文本框序列
与传统检测方法相比:
- 文本有各种各样的字符或文字,没有一个清晰明确的边界可以把它们作为整体框起来;
- 对位置异常敏感,直接预测位置错误率高,尤其水平位置,如下图:
![]()
使用Bounding Box回归预测文本框中心点坐标和高度
为了避免传统方法的问题,CTPN在做BBox回归时采用以下巧妙的Proposal生成方式:
把生成一个候选框变成生成一系列候选框,并且不关心候选框是框柱了一个完整的字;
不回归四个坐标,而只回归y轴坐标(中心点与高度)和预测当前候选框中是否为文字;
对任何一个候选框,使用k个Anchor(例如k=10)。 原理如图:
![]()
将文本框序列做合并,构造一整行文字BBox
基本原理为:
按照水平坐标从左到右排序Anchor;
依次计算两个Anchor的距离值distance(b1,b2) ;
distance(b1,b2)计算方法:水平正方向寻找与b1水平距离小于50个像素的Anchor;挑出与其垂直方向重合度大于0.7的Anchor;挑出符合上述条件的score值最大的Anchor即为b2。
最后,利用距离值计算生成连通图,连通图停止生长输出BBox。
![]()
以行驶证识别为例的行检测效果:
![]()
![]()
11.3.2 行识别模型算法思路
在文本行被检测出来有两种做法,1、切割每个字,然后做字符分类;2、直接对行做分类识别。CTPN采用第二种方式。
1、 整体思路是:
利用CRNN+CTC loss构建神经网络,令特征提取、序列建模和转写在一个统一框架中进行,其特点是:
不需要手工特征生成或预处理,End to End训练;
直接从序列学习,不需要精细化标注
可处理高度统一的任意长度字符串而不用做字符分割或尺度归一化
与词典本身关系不大
产生模型相对小故占用存储空间小,Training和Inference效率不错
当时取得了State of art效果
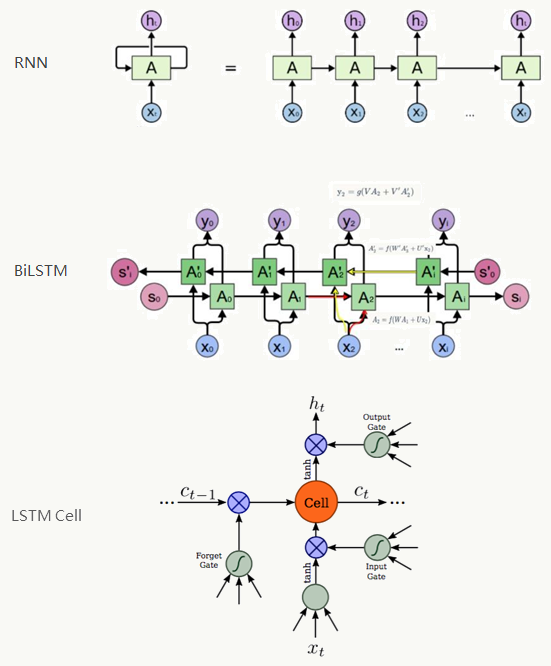
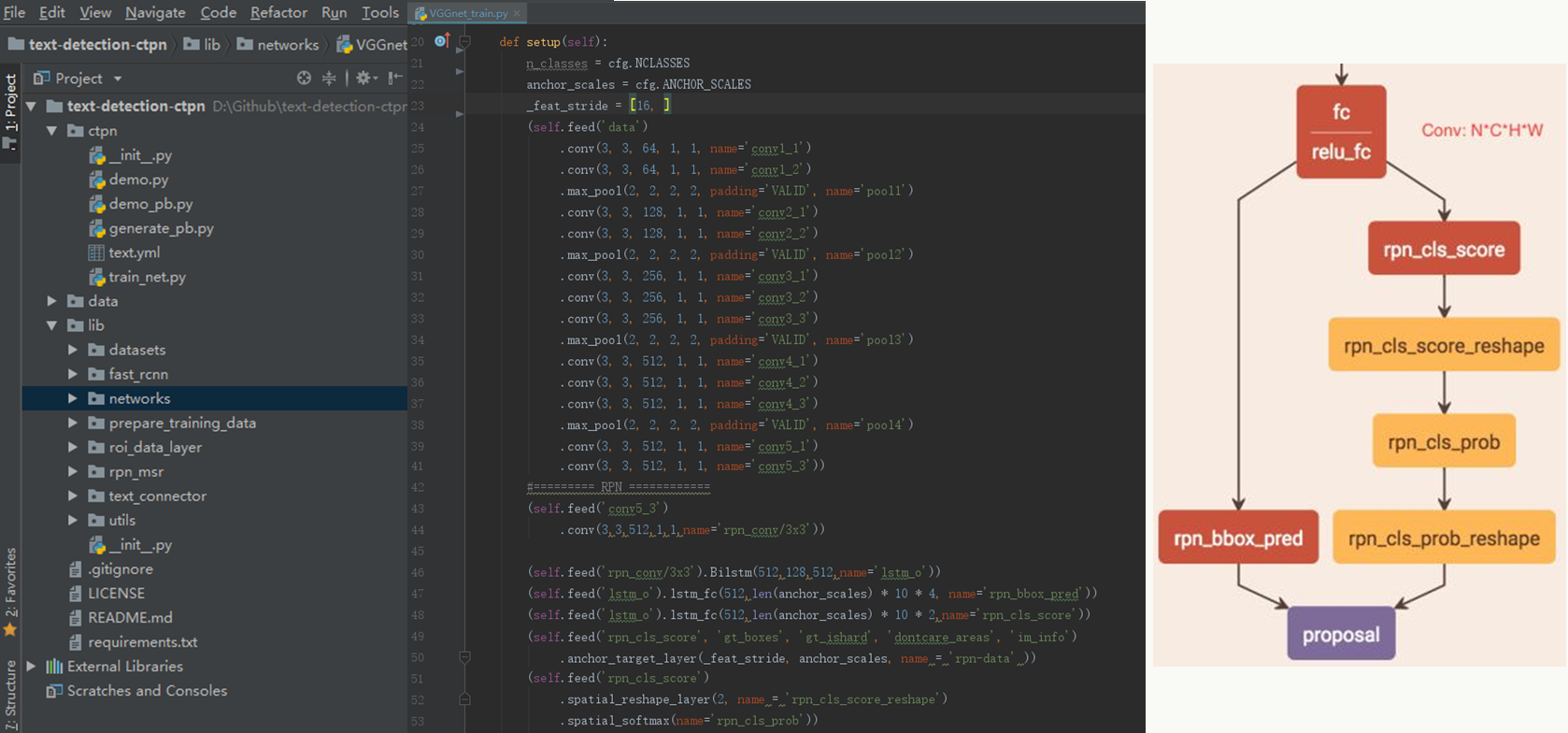
2、基于CRNN的行识别原理如下:
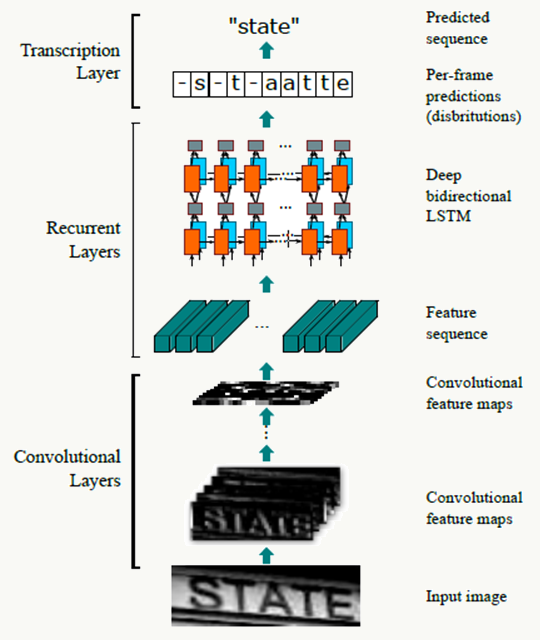
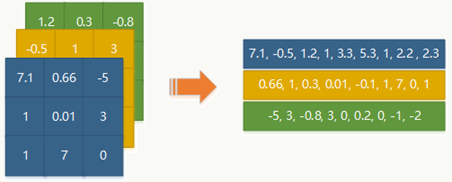
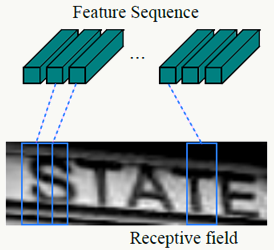
3、特征序列抽取
- 采用纯卷积和池化操作提取特征
- 所有图像Resize到相同高度
- 每列的宽度固定为单个像素
- 所有Feature Map的第i列组成的向量会成为RNN层的输入
![]()
- 平移不变性,Feature Map每列对应一个感受野
![]()
4、序列标注
- 充分利用文本的上下文信息
- RNN支持将误差反向传播至输入,循环层和卷积层可以共用一套训练框架
- 支持任意长度字符序列操作
- 使用LSTM除了解决传统RNN的Gradient Vanishing问题,还可以捕捉长距离语义依赖
![]()
5、转写
将RNN做的每帧预测转换成标签序列的过程。
利用CTC(它会删除所有重复字符),根据每帧预测找到具有最高概率的标签序列
可以基于字典或不基于字典做转写,前者受到字典约束