6. 循环神经网络与Transformers
6.1 RNN
6.1.1 基本原理
序列类问题是我们日常生活中常见的一类问题:我们读的文章,我们说话的语音等等,要么是在空间上的序列,要么是在时间的序列,序列的每个单元之间有前驱后继的语义或序列相关性,比如:当我们说,“这是我们伟大的××”,这里××是“祖国”的概率远远大于“板凳”,所以在NLP领域,应用大概可以分为几种:
1、根据当前上下文语义预测接下来出现某个文本的概率;
2、通过语言模型生成新的文本;
3、文本的通用NLP任务,例如词性标注、文本分类等;
4、机器翻译;
5、文本表示及编码解码。
传统的神经网络并没有很好的解决这种序列问题,于是Recurrent Neural Networks这种网络被提了出来: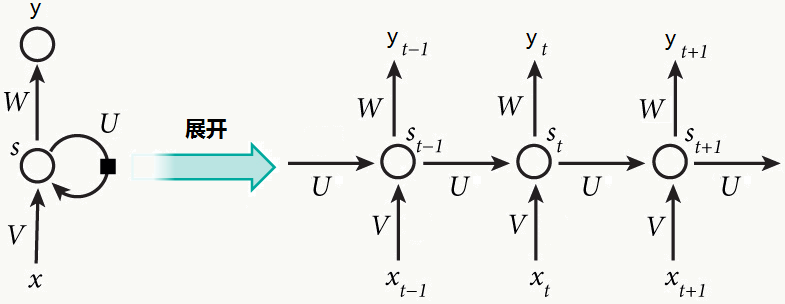
乍一看就是节点自带环路的网络,广义来看,可以在这个节点上展开,只是这种展开和输入的字数有关,比如输入为10个字,则展开10层。
从一个角度看,不同于传统神经网络会假设所有输入及输出是相互独立的,RNN正相反,认为节点间天然有相关性;另一个角度是,认为RNN具有“记忆”能力,它能把历史上相关节点状态“全部”记住,但实际情况是,我们当前说的一句话和较久前说的话未必有很强的关系,如果“全部”记住,一没必要、二计算量巨大。
6.1.2 BPTT 原理
以最简单的RNN为例,说明背后算法原理: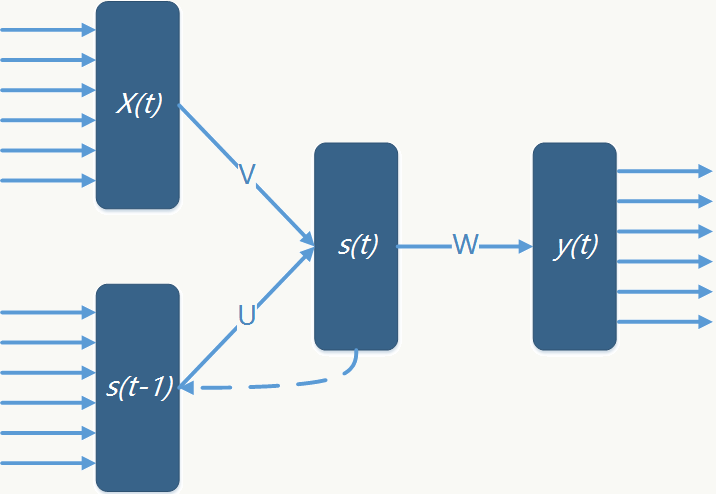
定义以下符号: \(x_i(t)\):输入层第\(i\)个节点;
\(s_h(t-1)\):前一个状态的隐藏层第\(h\)个节点;
\(s_j(t)\):当前状态的隐藏层第\(j\)个节点;
\(y_k(t)\):输出层第\(k\)个节点;
\(V\):输入层到隐藏层权重矩阵;
\(U\):前一状态隐藏层到后一状态隐藏层权重矩阵;
\(W\):隐藏层到输出层权重矩阵;
\(f\):隐藏层激活函数;
\(g\):输出层激活函数。
网络的前向传播关系为:
- 输入层到隐藏层
\[net_j(t)=\sum_{i=0}^nx_i(t)v_{ji}+\sum_{h=0}^m s_h(t-1)u_{jh}+b_j\] \[s_j(t)=f(net_j(t))\] 常用的\(f\)函数为Sigmoid类函数,如:\[f(net)=\frac{1}{1+e^{-net}}\]
- 隐藏层到输出层
\[net_k(t)=\sum_{j=0}^ms_j(t)w_{kj}+b_k\] \[y_k(t)=g(net_k(t))\]
常用的\(g\)函数为指数族函数,如:
\[g(net_k)=\frac{e^{net_k}}{\sum_pe^{net_p}}\]
这里需要注意的一个关键点是:\(U\)、\(V\)、\(W\)权重矩阵在不同时刻是共享的。
网络的反向传播关系:
只要网络的损失函数可微,那么任意一个前馈神经网络都可以通过误差反向传播(BP)做参数学习,BP本质是利用链式求导,使用梯度下降(GD)算法的最优化求解过程,而翻看前面第四章最优化原理,其求解就是给定目标函数,确定搜索步长和搜索方向的故事,GD的权重更新公式为(其中O为目标函数): \[\Delta w=-\eta \frac{\partial(O)}{\partial(w)} \]
同样回看第四章,目标函数多种多样,比如常见的有: SSE:\[O=\frac{1}{2}\sum_i\sum_j(\hat{y}_{ij}-y_{ij})^2\] cross entropy:\[O=\sum_i\sum_j\hat{y}_{ij}ln(y_{ij})+(1-\hat{y}_{ij})(1-lny_{ij})\]
但不管哪种目标函数,一般总可以分为线性部分(变量的线性组合)和非线性部分(激活函数),显然求导过程中线性部分最简单,非线性部分最复杂,所以上述权重更新公式可以拆解为:
\[\Delta w=-\eta \frac{\partial(O)}{\partial(net)}\frac{\partial(net)}{\partial(w)} \] 显然:\(\frac{\partial(net)}{\partial(w)}\)很容易计算,而\(\frac{\partial(O)}{\partial(net)}\)比较难计算,定义: \(\delta=-\frac{\partial(O)}{\partial(net)}\)为每个节点的误差向量,那么整个权重的更新核心考量就是怎么计算和传播\(\delta\)。
- 输出层任意一个节点\(k\)
\[ \delta_{pk}=\frac{\partial(O)}{\partial(y_{pk})}\frac{\partial(y_{pk})}{\partial(net_{pk})}=\frac{\partial(O)}{\partial(y_{pk})} g^{'}(s_{pk}) \]
- 隐藏层任意一个节点\(j\)
\[ \delta_{pj}=-(\sum_k^m\frac{\partial(O)}{\partial(y_{pk})}\frac{\partial(y_{pk})}{\partial(net_{pk})}\frac{\partial(net_{pk})}{\partial(s_{pj})})\frac{\partial(s_{pj})}{\partial(net_{pj})}=\sum_k^m\delta_{pk}w_{kj}f^{'}(s_{pj}) \]
基于以上推导得到:
- 当前状态隐藏层到输出层权重更新公式
\[\Delta w_{kj}=\eta \sum_p^m \delta_{pk}s_{pj} \]
- 输入层到当前状态隐藏层权重更新公式
\[\Delta v_{ji}=\eta \sum_p^n \delta_{pj}x_{pi} \]
- 上一状态隐藏层到当前状态隐藏层权重更新公式
\[\Delta u_{ji}=\eta \sum_p^m \delta_{pj}s_{ph}(t-1) \]
- 任一隐层在某个时间状态下的误差
注意,有意思的来了:
对RNN做展开后如图:
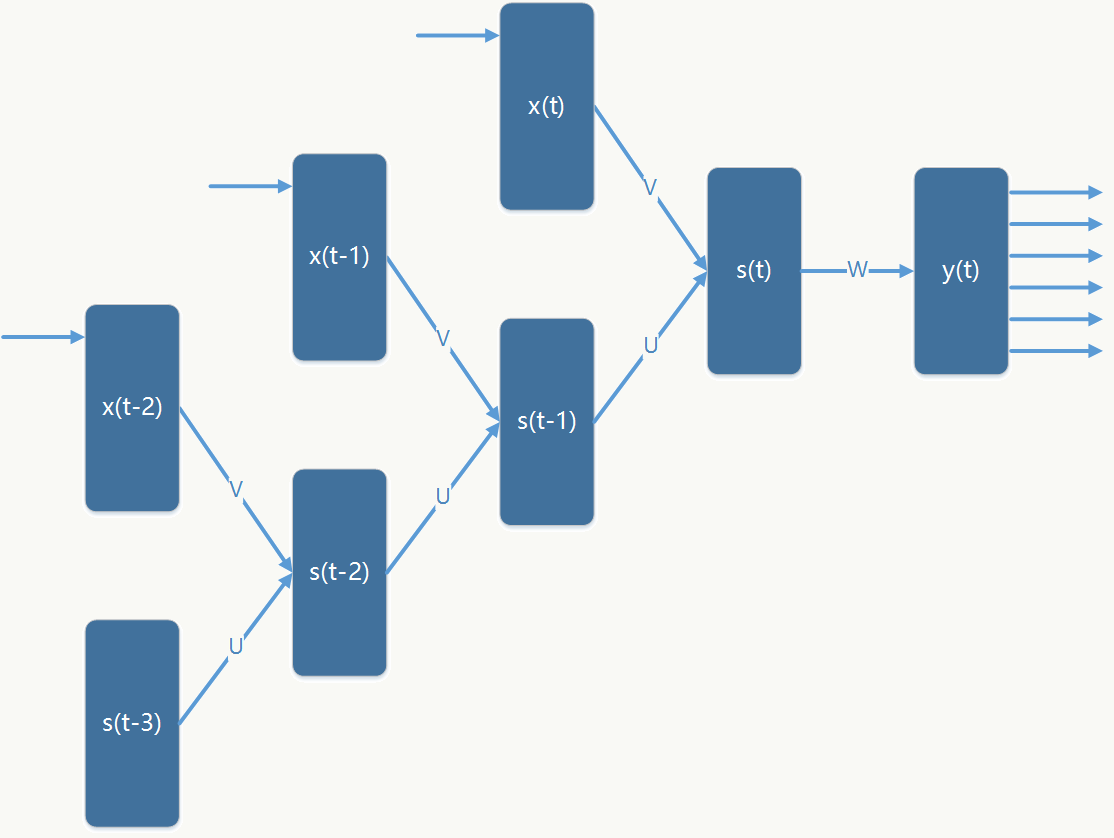
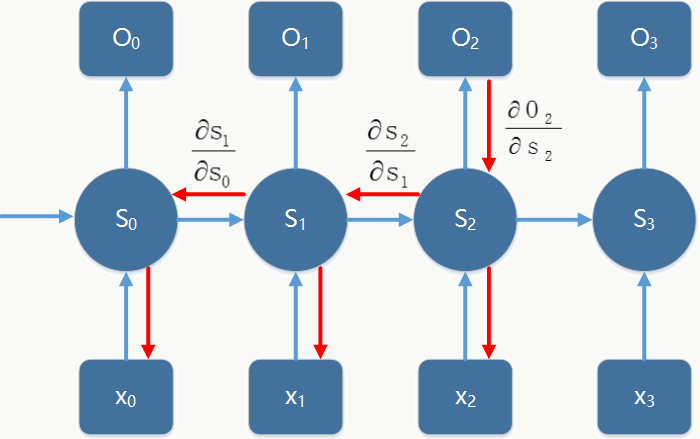
于是误差反向传播公式变为:
\[ \delta_{pj}(t-1)=-(\sum_h^m\frac{\partial(O)}{\partial(y_{ph})}\frac{\partial(y_{pk})}{\partial(net_{pk})}\frac{\partial(net_{pk})}{\partial(s_{pj})})\frac{\partial(s_{pj})}{\partial(net_{pj})}=\sum_h^m\delta_{ph}(t)u_{hj}f^{'}(s_{pj}(t-1)) \] 其中:\(h\)是在\(t\)时刻的任何一个隐层节点,\(j\)是在\(t-1\)时刻的任何一个隐层节点,高层的\(\delta\)可以通过循环递归的计算出来,所有\(\delta\)计算完毕后累加求和并应用在\(U\)、\(V\)的权重更新中。
6.1.3 代码实践
问题描述:给定一个字符,生成(预测)之后的n个字符,并使得整个句子看上去有语义含义。
1、训练数据生成如下图:

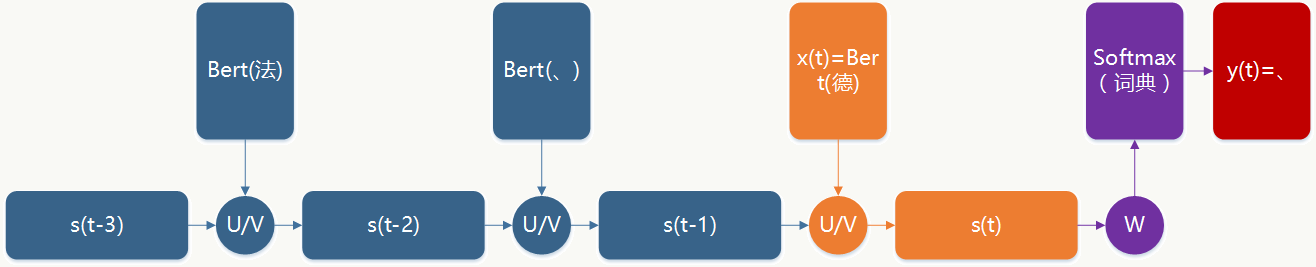
1 | # -*- coding:utf-8 -*- |
训练及测试结果:
1 | [Debug] iteration 0, loss value: 28.059744 |
6.2 混沌理论
关于混沌(Chaos)一词,西方和东方在哲学认知和神话传说上惊人的相似。例如古希腊神话中描述的:万物之初,先有混沌,是一个无边无际、空空如也的空间,在发生某种扰动后,诞生了大地之母Gaea等等,世界从此开始。中国古代神话中,天地未开之前,宇宙以混沌状模糊一团,盘古开天辟地后世界从此开始。
而在现代自然科学中,混沌理论的发展反映了人们对客观世界认知一步步演化的过程。人类对自然规律的认知,也从确定性(Deterministic)认知主导逐步演进到概率性(Probabilistic)认知主导。
经典力学与机械决定论
牛顿1686年创立了基于万有引力定律和三大定律的古典力学,即:第一定律,在沒有被外力作用下的物体,会保持静止或匀速直线运动状态;第二定律,物体的加速度与物体所受外力的合力成成正比,与物体本身的质量成反比,且加速度方向与合力方向相同;第三定律,两个物体间的作用力和反作用力大小相等方向相反。牛顿的这种基于确定性认知的绝对时空观在很长一段时间占据主导位置,例如拉普拉斯甚至认为:没有什么是不确定的,宇宙的现在是由其过去决定的,只要给定初始条件,智者可以用一个公式概括整个宇宙,预测宇宙未来的发展。拉普拉斯对于概率论有着巨大的贡献,但他认为概率论只是对决定论的补充而已。
三体问题
在那个年代,虽然人们对太阳、地球、月亮的运动规律了解的比较清楚,但对三个天体在长时间运动过程中,状态是否保持稳定、能否永远稳定运行等相关问题却没有什么认知,即理论上认为确定性的事情,而事实上却无法用已知的数学模型表达,这个就是天体力学中的经典模型——三体问题。19世纪末,人们已经知道,在一般三体问题中每个天体在其他两个天体引力作用下的运动方程都可以表示成6个一阶常微分方程,这意味着总共需要求18个完全积分才能获得完整解析解,而理论上只能得到10个完全积分,即描述三个或三个以上天体运动的方程组不可积分,更不能得到解析解。 虽然后来欧拉和拉格朗日分别在给定约束条件下求得了限制性三体问题的5个特殊解,即著名的拉格朗日点,但通用三体问题依然无解。
庞加莱的错误
庞加莱(就是那个提出庞加莱猜想的庞加莱)在1887年参加瑞典国王发起的“太阳系是稳定的么”的竞赛中,对限定性三体问题发表了一篇论文,初稿出来后,一个名叫弗拉格曼的26岁年轻人发现了其中有不明确的部分,而庞加莱在修改过程中发现了原来的证明有错误,于是在深思熟虑后彻底抛弃了原来通过定量分析求解的方法,转而以定性分析求解并成功给出三体问题的定性解答,而那个错误是由于初始条件的微小误差导致最终结果的南辕北辙,这个观察清晰而定性的开辟了混沌理论。
蝴蝶效应
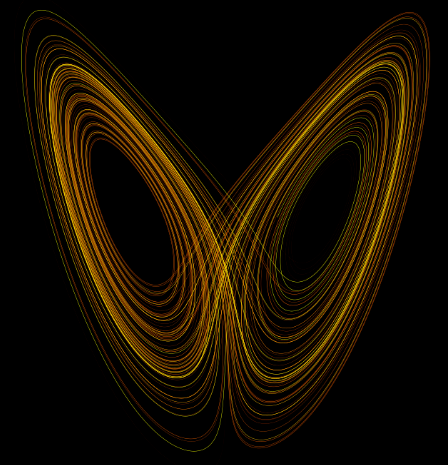
现代科学史中,真正意义上的混沌理论是MIT的洛伦茨(Lorenz)提出的,在此之前人们原本以为,只要配上动力学公式和超级计算机,就能模拟出自然界的各种现象,1961年,洛伦茨用Royal McBee LGP-30计算机(16k内存,每秒60次乘法运算)做气象动力学模拟实验时,由于一个偶然的对初始值做四舍五入的处理,导致模拟结果大相径庭。基于这次实验,1963年,洛伦茨在《气象学报》发表了《確定性的非周期流》系列,以物理意义更加明确的数学模型表示和发展了混沌理论。
![]() 洛伦茨系统
洛伦茨系统
简单看一个关于流体热力传导的问题:
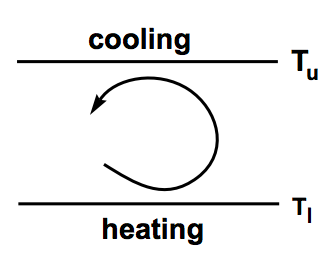
当温差较小时,热力会以传导的方式从热的板块到冷的板块,当温差较大时,下面的暖流体上升,上面的冷流体下沉,冷、热板块会产生对流滚动。针对这个问题,洛伦茨将他原始方程中除三个傅立叶系数外的其他系数都设为0,得到了简化的微分方程:
\[ \begin{align*} & \dot{x}=-\sigma x+\sigma y \\ & \dot{y}=-xz+rx-y \\ & \dot{z}=xy-bz \\ \end{align*} \]
其中\(\sigma\)是Prandtl系数、\(r\)是Rayleigh系数、\(b\)是系统参数,决定了循环的宽度(图中\(T_u\)与\(T_l\)质检的距离)、\(x\)与循环流体的流苏成正比,且\(x>0\)时流体顺时针对流,\(x<0\)时流体逆时针对流、\(y\)与温差成正比、\(z\)与垂直温度曲线与平衡温度曲线的失真成正比。
洛伦茨发现,当\(\sigma=10\)且\(b=8/3\)时,只要Rayleigh系数超过\(r\approx 24.74\),系统就会表现为"混沌",即所有的解似乎对初始条件都很敏感,几乎所有的解显然既不是周期性解,也不收敛于周期性解。换句话说,洛伦茨用一个确定性的方程告诉我们一个热力学动态系统的不可预知性。
回想电视剧里看到的离奇故事:
1、因为一滴雨水掉在了马的眼睛里,马摔倒了;
2、恰好骑马的是一名斥候,斥候受伤了;
3、斥候受伤导致手上的情报没有被及时送到军营,军队战败了;
4、军队战败导致重要城市丢失,敌军长驱直入进入都城;
5、都城被灭,皇帝被杀,国家灭亡。
混沌理论的核心思想是:初始条件的微小差别或变化,可以导致最终结果发生剧烈的变化。
下面从理论方面做一些简单介绍,帮助理解未来我们会用到的一些概念。
6.2.1 一维映射
1、动态系统(Dynamical System)
一个动态系统由一组可能的状态组成,再加上一个用过去的状态来确定现在的状态的规则。最典型的动态系统是时间离散动态系统(discrete-time dynamical system)和时间连续动态系统(m continuous-time dynamical system),前面我们介绍的RNN就是一种离散动态系统。
很多现实当中问题往往是随着时间演化的动态系统,例如:模拟细菌生长过程,在给定初始细菌数后,随着时间流逝,细菌数量增长的模型如下:
\[x_n=f(x_{n-1})=2x_{n-1}=f(f(x_{n-2}))=f^n(x_0)=2^nx_0\] \(x_0\)表示初始细菌数,\(n\)表示随时间演化,显然这个增长过程是以指数增长的。
2、固点(Fixed Points) 如果动态系统有映射\(f\),且满足\(f(p)=p\),则\(p\)被称为固点。还以上面细菌生长过程为例,几何意义如下图表示: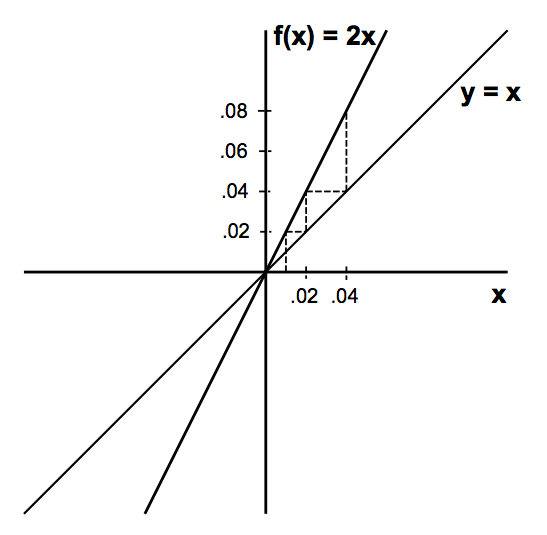
利用\(y=x\)直线发现动态系统的固点只有x=0这一点,画出动态系统的演化轨迹(虚线部分),随着时间流逝,细菌种群规模趋向于正无穷。
但真实情况是,受限于环境、资源等因素,细菌种群规模不可能无限大,所以修改动态系统为: \[x_n=f(x_{n-1})=2x_{n-1}(1-x_{n-1})=f(f(x_{n-2}))=f^n(x_0)\]
几何意义如下图表示: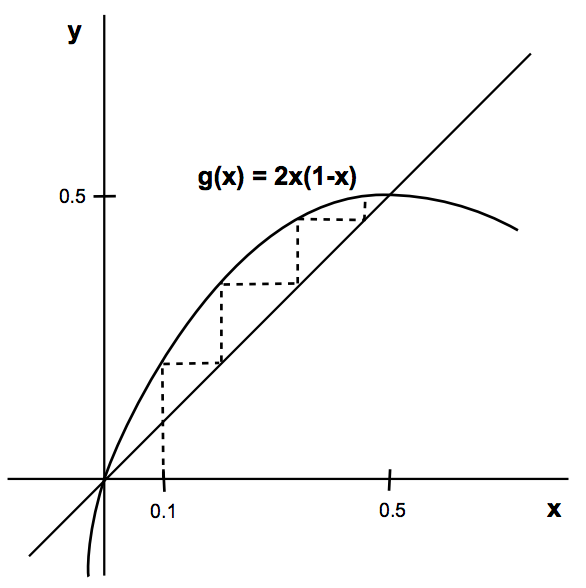
利用\(y=x\)直线发现动态系统的固点有x=0和x=0.5这两个点,画出动态系统的演化轨迹(虚线),随着时间流逝,不管初始种群\(x_0\)取多少,细菌种群规模最终趋向于0.5(被吸引到0.5),用R做个简单模拟:
1 | g <- function(x){ |
部分结果如下:
| t | y(x=0.941631) | y(x=0.6455615 ) | y(x=0.1207315 ) |
|---|---|---|---|
| 1 | 0.1099241 | 0.4576237 | 0.2123107 |
| 2 | 0.1956815 | 0.4964085 | 0.3344698 |
| 3 | 0.3147805 | 0.4999742 | 0.4451995 |
| 4 | 0.4313875 | 0.5 | 0.4939938 |
| 5 | 0.4905846 | 0.5 | 0.4999279 |
| 6 | 0.4998227 | 0.5 | 0.5 |
| 7 | 0.4999999 | 0.5 | 0.5 |
| 8 | 0.5 | 0.5 | 0.5 |
| 9 | 0.5 | 0.5 | 0.5 |
| 10 | 0.5 | 0.5 | 0.5 |
3、稳定的固点(Stability of Fixed Points)
假设动态系统的映射为\(f(x) =\frac{(3x-x^3)}{2}\),几何形态如下:
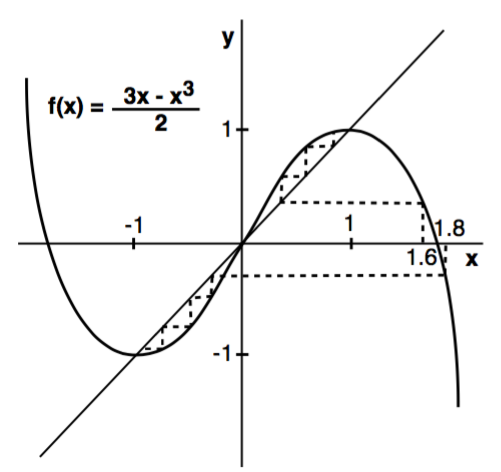
利用\(y=x\)直线发现动态系统的固点有\(x_0=0\)和\(x_1=1\)和\(x_2=-1\)这三个点,画出动态系统的演化轨迹(虚线),其中\(x_1\)和\(x_2\)两个点被称为稳定固点,在\(x_1\)和\(x_2\)两个值的某个邻域内,y会分别收敛于1和-1两个值,\(x_0\)为不稳定固点,在它的+邻域内y会被推到上半区,-邻域内y会被推到下半区。
4、吸引固点(Sink)与排斥固点(Source)
首先对点\(p\)定义它的邻域:
\[N_\epsilon(p)=\{x\in R:|x-p|<\epsilon\},0<\epsilon<<1\]
其次,假设动态系统有映射\(f\),点\(p\)为实数值,且满足\(f(p)=p\),如果存在\(p\)的邻域\(N_\epsilon(p)\),使得所有邻域内的点会被吸引到\(p\)点,即:
\[lim_{k->\infty}f^k(x)=p,x\in N_\epsilon(p)\]
则点\(p\)被称作Sink,反之如果邻域内的点会被排斥远离点\(p\),则点\(p\)被称作Source。
数学化表示如下,记住这个表示,未来解释为什么RNN无法利用梯度下降学到长依赖关系时会用到:
如果\(f\)是一个在实数集上的平滑映射,假设\(p\)是\(f\)的固点,则:
1、如果\(|f'(p)|<1\),则\(p\)是吸引固点Sink;
2、如果\(|f'(p)|>1\),则\(p\)是排斥固点Source。
证明: 假设\(\alpha\)是介于\(|f'(p)|\)和1之间的任意实数,对于:
\[lim_{x->p}\frac{|f(x)-f(p)|}{|x-p|}=|f'(p)|\] 存在一个\(p\)的邻域\(N_\epsilon(p),\epsilon>0\),使得:
\[\frac{|f(x)-f(p)|}{|x-p|}<a<1,(x\in N_\epsilon(p),x\neq p)\]
换句话说,相比\(x\),\(f(x)\)更接近\(p\),也说明,如果\(x\in N_\epsilon(p)\),则\(f(x)\in N_\epsilon(p)\),以此类推,\(f^2(x)\)、\(f^3(x)\)也满足此性质,归纳下变成: \[|f^k(x)-p|\leq\alpha^k|x-p|,k\geq 1\]
所以\(p\)是一个吸引固点Sink。
换一个角度,从一阶泰勒展开式或导数的定义来看:
在\(p\)点的一阶泰勒展开式: \[f(p+h)\approx f(p)+hf'(p)\]
1、如果\(|f'(p)|<1\),则\(p\)是吸引固点Sink;
2、如果\(|f'(p)|>1\),则\(p\)是排斥固点Source。
5、k周期点
举一个例子:\(f(x)=3.3x(1-x)\),其图形如下: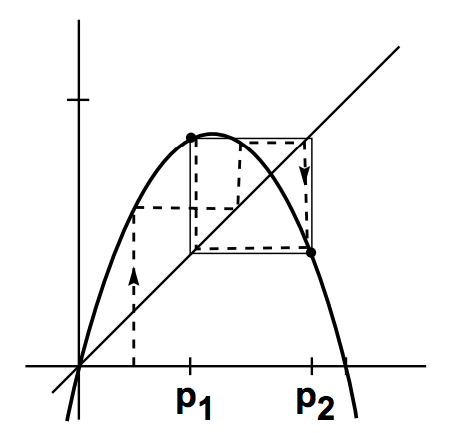
利用\(y=x\)直线发现动态系统的固点有\(x_0=0\)和\(x_1=\frac{23}{33}\)两个点,而这两个点都是排斥固点,那么吸引固点去哪儿了呢?做一个简单模拟:
1 | g <- function(x){ |
部分结果如下:
| t | y(x=0.1156445) | y(x=0.3317354) | y(x=0.0.9131461) |
|---|---|---|---|
| 1 | 0.3374938 | 0.7315672 | 0.2617241 |
| 2 | 0.7378527 | 0.6480429 | 0.6376411 |
| 3 | 0.6383061 | 0.7526749 | 0.7624812 |
| 4 | 0.7618757 | 0.6143128 | 0.5976419 |
| 5 | 0.5986897 | 0.7818775 | 0.793538 |
| 6 | 0.7928592 | 0.5627987 | 0.540657 |
| 7 | 0.5419706 | 0.8119858 | 0.8195451 |
| 8 | 0.8191869 | 0.5037939 | 0.48804 |
| 9 | 0.488795 | 0.8249525 | 0.824528 |
| 10 | 0.8245857 | 0.4765394 | 0.4774493 |
| 11 | 0.4773257 | 0.8231837 | 0.8233218 |
| 12 | 0.8233034 | 0.4803226 | 0.4800279 |
| 13 | 0.4800672 | 0.8237222 | 0.8236837 |
| 14 | 0.8236889 | 0.4791729 | 0.4792553 |
| 15 | 0.4792442 | 0.8235686 | 0.8235799 |
| 16 | 0.8235784 | 0.4795012 | 0.479477 |
| 17 | 0.4794803 | 0.8236133 | 0.8236101 |
| 18 | 0.8236105 | 0.4794056 | 0.4794125 |
| 19 | 0.4794116 | 0.8236004 | 0.8236013 |
| 20 | 0.8236012 | 0.4794332 | 0.4794312 |
一个有意思的现象出现,\(p_1=0.4694\)和\(p_2=0.8236\)交替出现且为吸引固点,换个角度就是:\(f(p_1)=p_2,f(p_2)=p_1;f^2(p_1)=p_1\),\(f^2(p_2)=p_2\),也就是吸引固点以2为周期出现,在两个点间循环往复。
形式化定义为:
假设动态系统有实数集上的映射\(f\),点\(p\)为实数值,且满足\(f^k(p)=p\),\(k\)为正整数,则\(p\)被称为k周期点。
扩展下之前吸引固点的定义到k周期点:
如果\(f\)是一个在实数集上的平滑映射,假设\(\{p_1,p_2,...p_k\}\)构成了\(f\)的\(k\)周期点,则:
1、如果\(|f'(p_k)...f'(p_1)|<1\),则\(\{p_1,p_2,...p_k\}\)是吸引固点Sink;
2、如果\(|f'(p_k)...f'(p_1)|>1\),则\(\{p_1,p_2,...p_k\}\)是排斥固点Source。
还是上面的那个例子:
\(f(x)=3.3x(1-x)\)
则有: \(f'(x)=3.3-6.6x\) k周期点为:\(\{0.4694,0.8236\}\)
因为\(|f'(0.4694)f'(0.8236)|=0.2904<1\),所以它是吸引固点。
6.2.2 二维映射
把一维映射扩展到多维映射,看看会出现什么有趣的现象,由于二维映射是多维映射的最简单形式且各种性质与多维映射一致,固以此为基础讨论。
1、邻域
扩展一维映射时的邻域概念如下:
在欧式空间实数域下,向量\(v=(x_1,x_2,......x_m)\)的范数定义为:
\[|v|=\sqrt{x_1^2+x_2^2+......+x_m^2}\]
对\(p=(p_1,p_2,......p_m)\)定义它的邻域:
\[N_\epsilon(p)=\{v\in \mathbb{R}^m:|v-p|<\epsilon\},0<\epsilon<<1\]
有时候也叫\(p\)的\(\epsilon\)-\(disk\),举个例子。
二维下(\(p=(1,1)\)):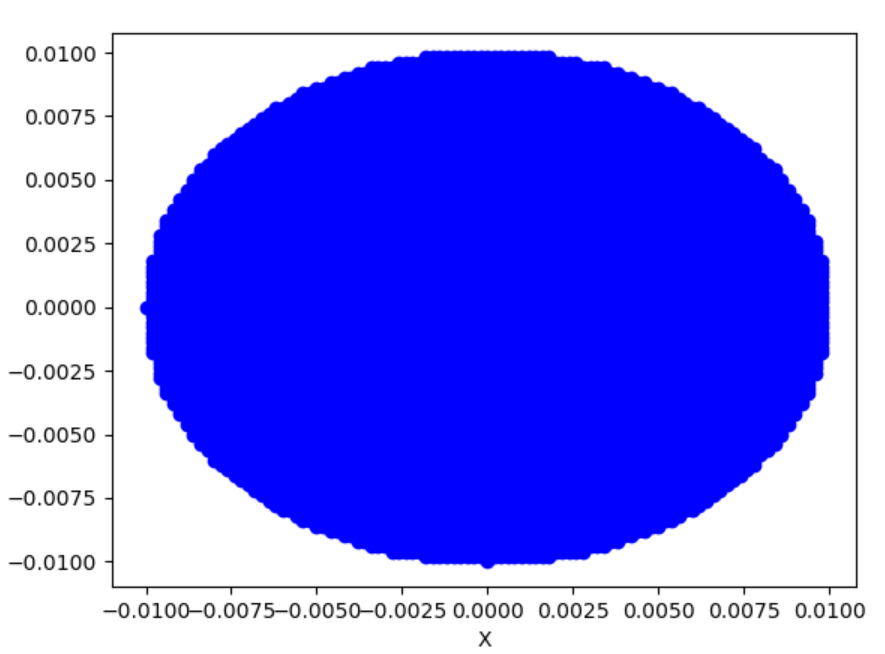
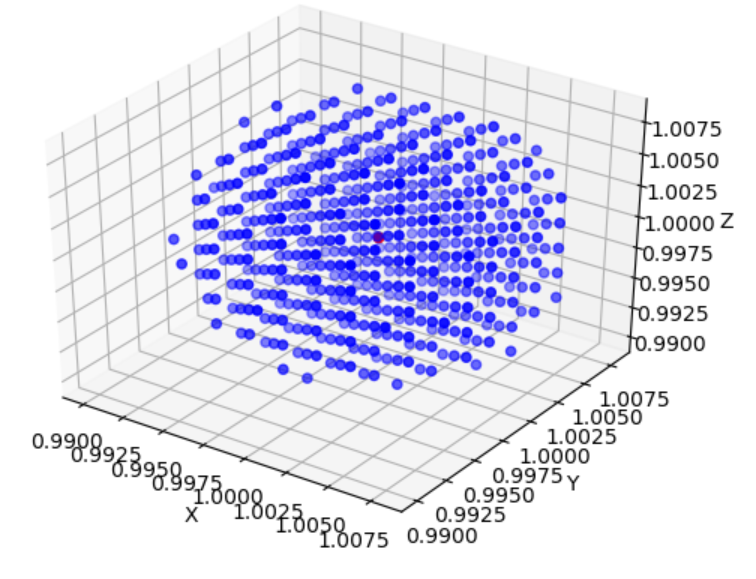
2、固点
其次,假设动态系统有实数域\(\mathbb{R}^m\)的映射\(f\),\(p\)为实数域\(\mathbb{R}^m\)固点,即满足\(f(p)=p\),如果存在\(p\)的邻域\(N_\epsilon(p)\),使得所有邻域内\(v\)会被吸引到\(p\),即: \[lim_{k->\infty}f^k(v)=p,v\in N_\epsilon(p)\]
则\(p\)被称作Sink,反之如果邻域内的点会被排斥远离点\(p\),则点\(p\)被称作Source。
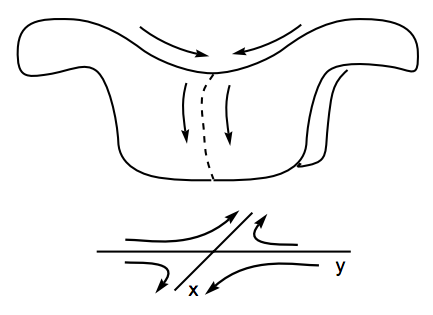
在二维映射下还会出现一个一维映射时不会出现的固点,叫做鞍点(Saddle),可以把它看做介于吸引固点和排斥固点间的一种状态,它拥有至少一个吸引方向和至少一个排斥方向。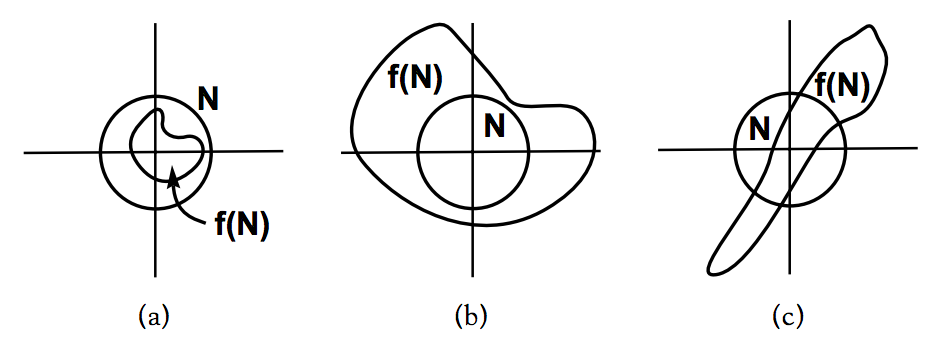
图中\(f\)代表映射,\(N\)代表\(p\)点的邻域。\(a\)图代表\(p\)是一个吸引固点,进入其邻域的点会被吸引到\(p\)点、\(b\)图代表\(p\)是一个排斥固点,进入其邻域的点会被排斥而远离\(p\)点、\(c\)图代表\(p\)是一个鞍点,进入其邻域的点先会被吸引到\(p\)点,然后会被排斥而远离\(p\)点。来个更直观的图:
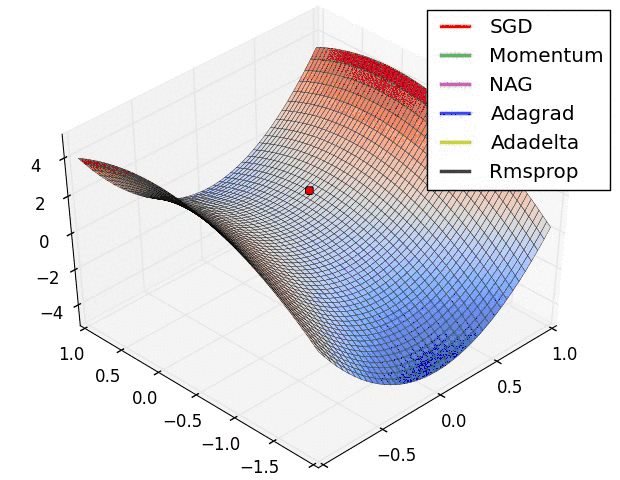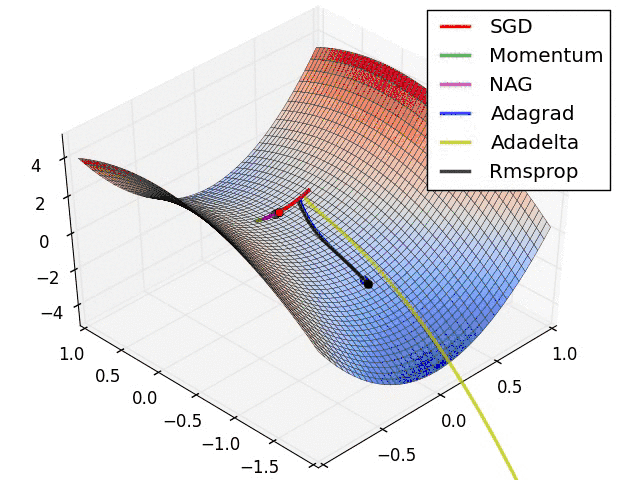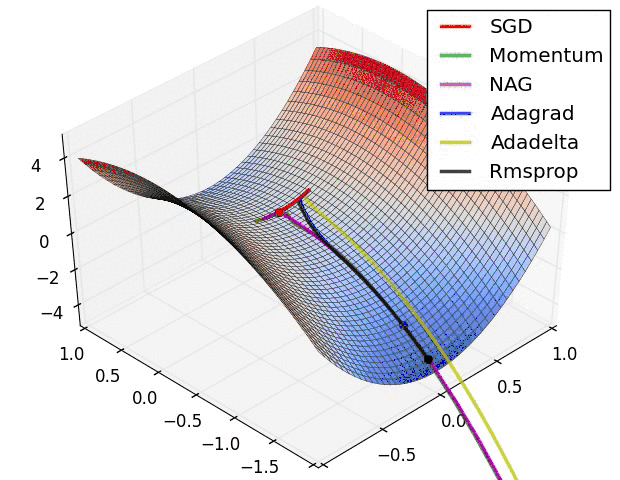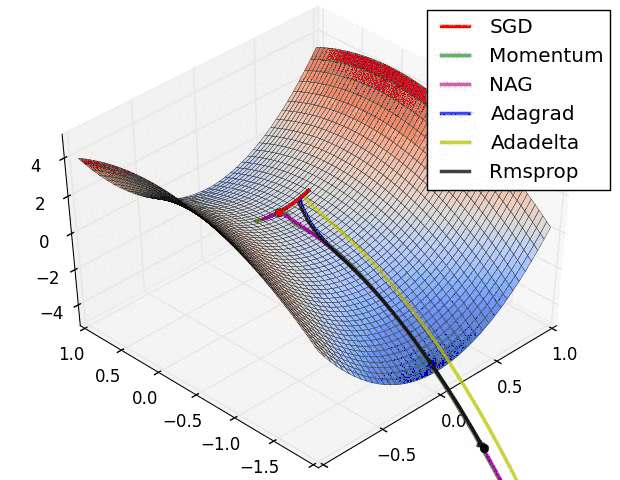
在《最优化原理-梯度下降》这一章我们曾经介绍过常用的一阶最优化方法,给定初始值后,不同的优化方法的优化轨迹不一样,但大的方向都是先被迭代吸引到鞍点,然后再从鞍点被排斥走,而因为待优化问题往往有很多局部最优点,所以我们希望优化算法能尽可能跳出当前点去寻找更优的局部最优点。
综上所述,显然排斥固点Source和鞍点Saddle的最大特点是:它们都是固点,都不是稳定固点,因为它们对初始条件很敏感,但对研究一个动态系统它们很重要。
6.2.3 线性映射
1、线性映射
所谓线性映射是指:
给定实数\(a,b\in \mathbb{R}\)及实数向量\(v,w \in \mathbb{R}^m\),有\(\mathbb{R}^m\to \mathbb{R}^m\)的映射\(A(v)\)满足: \[A(av+bw)=aA(v)+bA(w)\] 显然原点(0,0)是所有线性映射的固点,且是稳定的,如果它邻域内的点在迭代映射时都趋向于接近固点,则该固点是一个吸引子,稍微正式点的定义如下:
在一个随时间演变的动态系统中,吸引子是一个代表某种稳定状态的数值集合,在给定动态系统初始状态后,系统有着朝该集合所表示的稳态演化的趋势,在吸引子的某个邻域(basin of attraction)范围内,即使系统受到扰动,也会趋向于该稳态。
后面会大量出现吸引子这个概念。
2、鞍点
如果实数\(\lambda\)和实数向量\(v\)满足:
\[Av=\lambda v\] 则它们分别被称为A的特征值和特征向量。
假设有以下向量关系:
\[v_{n+1}=Av_n\]
则有递推关系:
\[ \begin{align*} & v_1=Av_0=\lambda v_0 \\ & v_2=Av_1=\lambda v_1=\lambda^2v_0 \\ & ...... \\ & v_{n+1}=\lambda^n v_0\\ \end{align*} \] 以\(\mathbb{R}^2\)上的映射为例:
\[A(x,y)=(ax,by)\]
表示成矩阵形式: \[ Av= \left[ \begin{matrix} a & 0 \\ 0 & b \end{matrix} \right] \left[ \begin{matrix} x\\ y \end{matrix} \right] \] 以上过程迭代了\(n\)次后得到: \[ A^n= \left[ \begin{matrix} a^n & 0 \\ 0 & b^n \end{matrix} \right] \]
这里就有意思了,\(A\)迭代了\(n\)次后,把它映射在一个二维平面上,看上去应该是个椭圆形,其中横坐标长度为\(|a|^n\),纵坐标为\(|b|^n\),对于原点的某个邻域\(N_\epsilon(0,0)\)同样也是个椭圆,横纵坐标长度分别为\(\epsilon|a|^n\)和\(\epsilon|b|^n\),假设\(n\to \infty\),则会有三种情况:
1、如果\(|a|,|b|<1\),则整个椭圆会收缩到原点(0,0),原点是Sink;
2、如果\(|a|,|b|>1\),则整个椭圆会无限过大并远离原点(0,0),原点是Source;
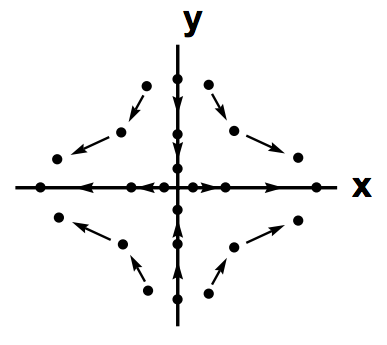
3、如果\(|a|>1>|b|\),则整个椭圆的横坐标会无限扩大,而纵坐标会收缩到0,此时原点既不是Sink也不是Source,人们把它叫做Saddle(鞍点)。
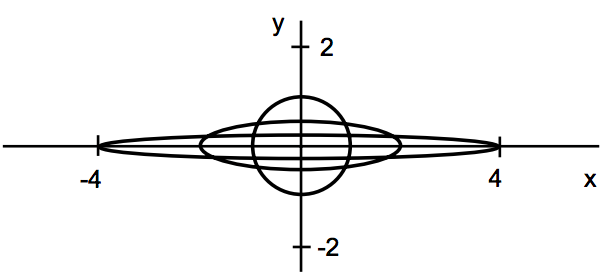
假设取:\(a=2,b=0.5\),则: \[ A= \left[ \begin{matrix} 2 & 0 \\ 0 & 0.5 \end{matrix} \right] \] 经过\(n\)次迭代后,得到下图:
3、双曲(hyperbolic)
假设A是实数域矩阵,基于它定义了\(\mathbb{R}^m\to \mathbb{R}^m\)的线性映射\(A(v)\),则:
如果\(A\)的所有特征值的绝对值都小于1,则原点是一个吸引固点Sink;
如果\(A\)的所有特征值的绝对值都大于1,则原点是一个排斥固点Source;
如果\(A\)的所有特征值中至少有一个其绝对值大于1,且最少有一个其绝对值小于1,则原点是一个鞍点Saddle。
如果一个映射\(A\),没有一个特征值的绝对值等于1,则我们把\(A\)叫做是双曲的,显然有三类双曲映射:Sink、Source、Saddle。
6.2.4 非线性映射
真实世界中,非线性系统远远多于线性系统,而当非线性程度足够高时,系统将出现混沌状态,不过从概念和定义上与线性映射区别不大。前面说的吸引固点和k周期吸引固点都是运动状态可预测的,它们被叫做平庸吸引子,而运动状态不可预测的叫做奇异吸引子(Strange Attractor)。
同样利用泰勒展开式,在非线性高维空间,导数被扩展为雅克比矩阵(Jacobian matrix):
\[f(p+h)\approx f(p)+Df(p)\cdot h\] 其中:
1、\(f=(f_1,f_2,......f_m)\)是\(\mathbb{R}^m\)上的映射,\(p\in \mathbb{R}^m\)
2、雅可比矩阵\(Df(p)\)为: \[Df(p)= \left[ \begin{matrix} \frac{\partial f_1}{\partial x_1}(p) & ...... & \frac{\partial f_1}{\partial x_m}(p) \\ \frac{\partial f_m}{\partial x_1}(p) & ...... & \frac{\partial f_ms}{\partial x_m}(p) \end{matrix} \right]\]
假设\(p\)为固点,满足\(f(p)=p\),则: \[f(p+h)\approx f(p)+Df(p)\cdot h=p+Df(p)\cdot h\] 即,在\(p\)点邻域内对其做一个微小扰动,输出会有\(Df(p)\cdot h\)的变化,显然类似线性映射,可以有下面结论:
假设:\(f\)是\(\mathbb{R}^m\)上的映射,且\(p\in \mathbb{R}^m\),满足\(f(p)=p\),则:
1、如果\(Df(p)\)没有取值为1的特征值,则\(p\)被称作双曲(hyperbolic)的,这个词很重要,会在后面多次出现,直观的也挺好理解,1的多少次方都还是1,只有大于1或小于1才会在某个方向上要么吸引要么排斥;
2、如果\(Df(p)\)的每个特征值的绝对值都小于1,那么\(p\)是一个吸引固点Sink,也有人叫做双曲吸引子(hyperbolic attractor);
3、如果\(Df(p)\)的每个特征值的绝对值都大于1,那么\(p\)是一个排斥固点Source;
4、如果\(m\geq 1\)且\(p\)是双曲的,\(Df(p)\)至少有一个特征值的绝对值大于1且至少有一个特征值的绝对值小于1,则\(p\)是一个鞍点Saddle。
举个例子:
有非线性映射:
\[f_{a,b}(x,y)=(-x^2+0.4y,x)\] 因为\(f(x,y)=(x,y)\),则有\(-x^2+0.4y=x\)且\(x=y\) 所以\(f\)有两个固点:\((0,0),(-0.6,-0.6)\)
其雅克比矩阵为:
\[Df(x,y)= \left[ \begin{matrix} -2x & 0.4 \\ 1 & 0 \end{matrix} \right] \]
于是:
\[Df(0,0)= \left[ \begin{matrix} 0 & 0.4 \\ 1 & 0 \end{matrix} \right] \]
特征值为:\(\pm\sqrt{4}\approx\pm0.632\)
\[Df(-0.6,-0.6)= \left[ \begin{matrix} 1.2 & 0.4 \\ 1 & 0 \end{matrix} \right] \]
特征值为:\(1.472\)和\(-0.272\),显然,\((0,0)\)为双曲吸引子,\((-0.6,-0.6)\)为鞍点。
6.2.5 混沌的演化及结构
用一个简单的抛物线做说明: \[y=1-rx^2 :0\leq r\leq 1;-1\leq x_n\leq 1\]
将其转化为迭代形式(一般来说,越复杂的非线性方程越无解析解,常常用数值计算中的迭代方法得到解):
\[x_{n+1}=1-rx_n^2\]
程序模拟迭代过程:
1 | import numpy as np |
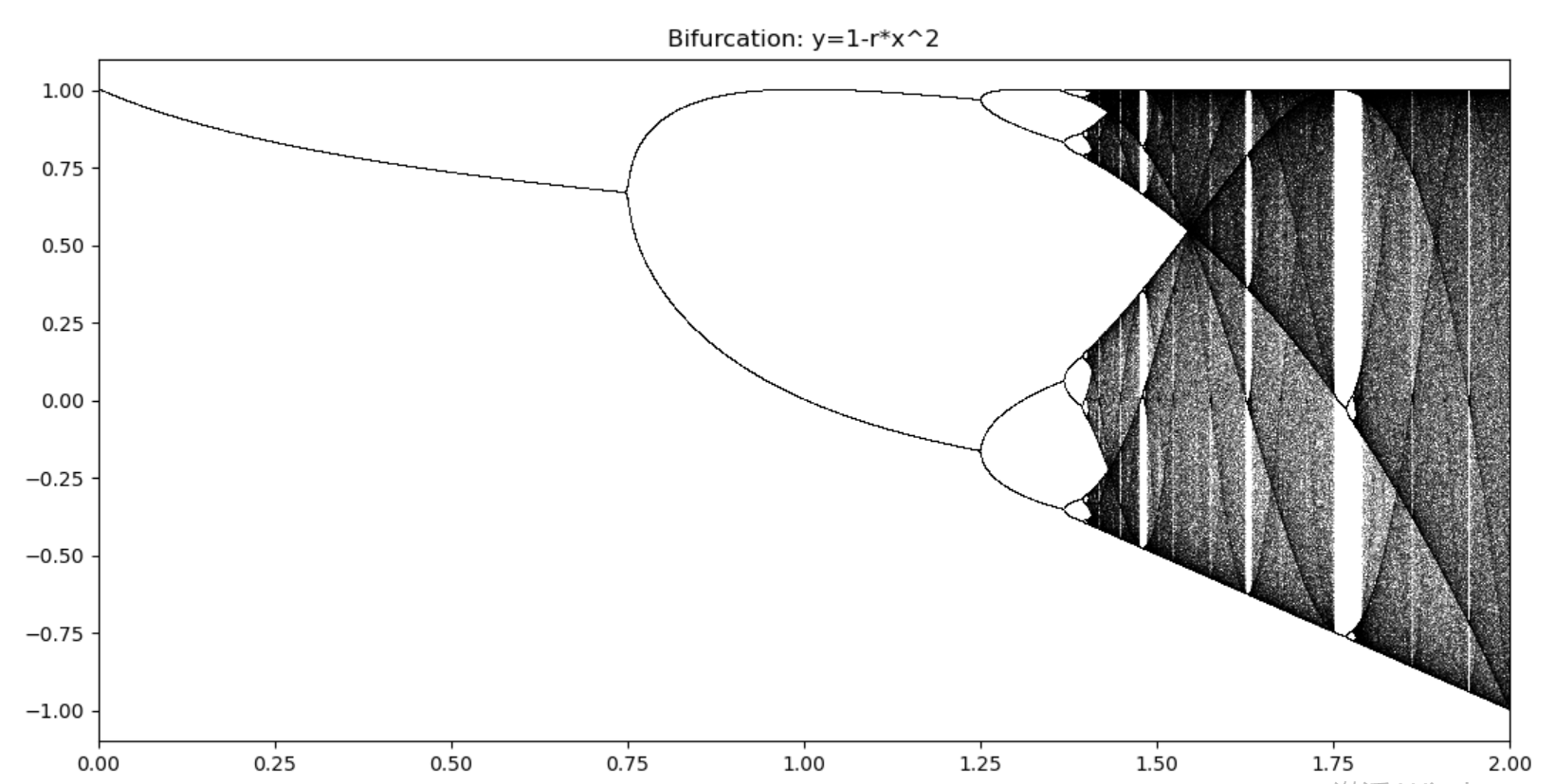
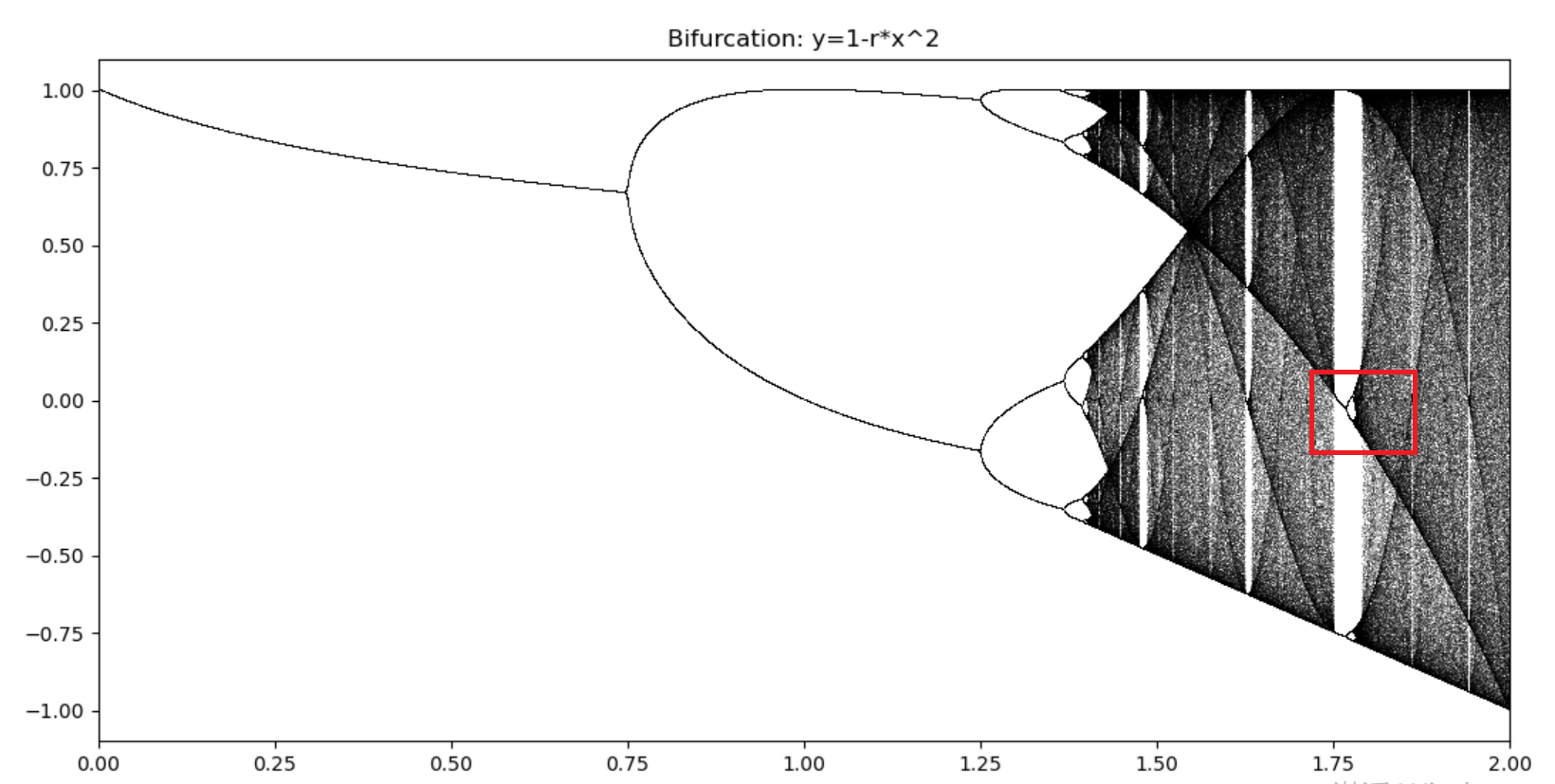
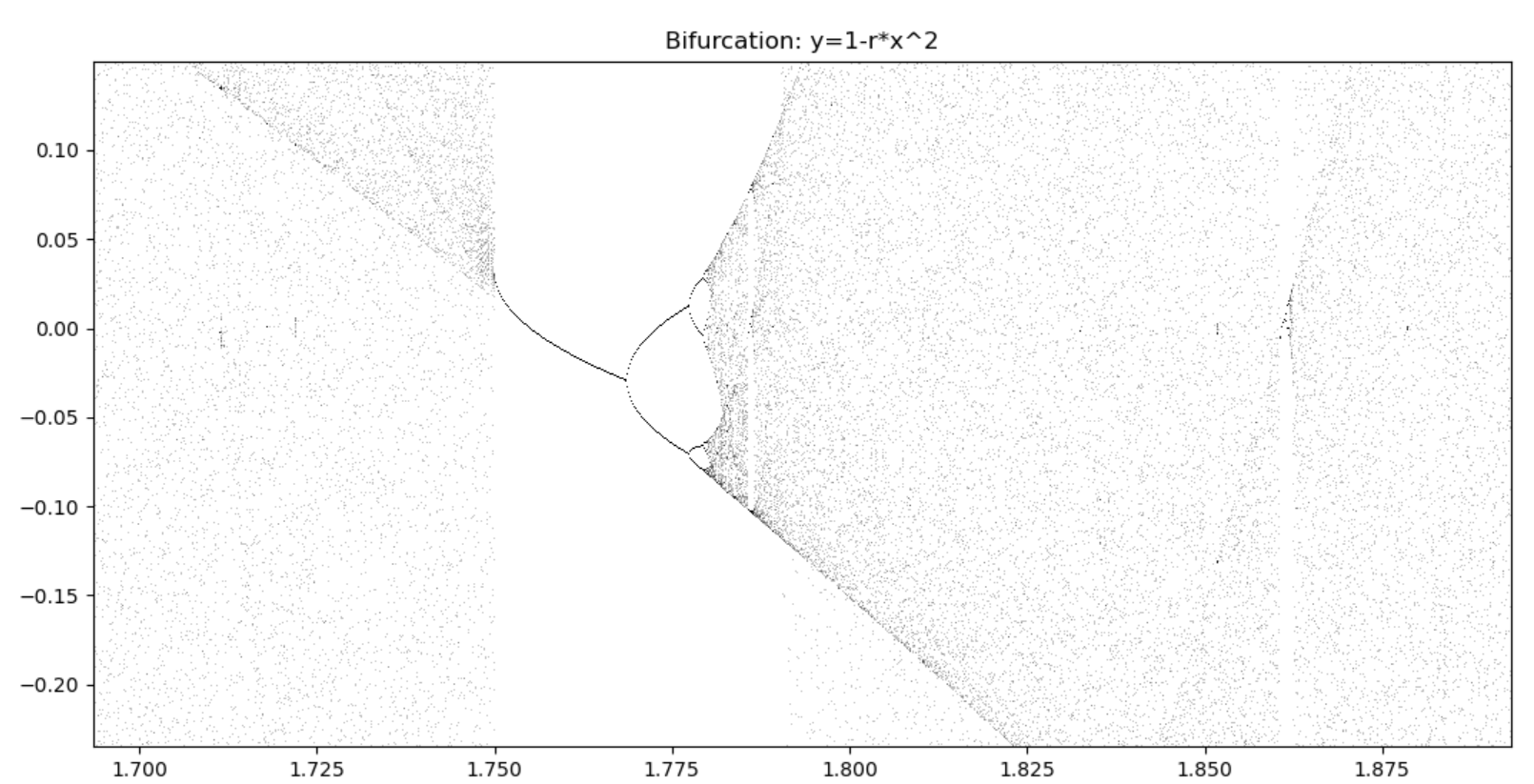
随着复杂度的提升,系统经历了:稳定态->周期态->类周期态->混沌态。
还可以再次放大类似的红框区域,但会发现一个普适的规律:
\[\delta=\lim\limits_{n->\infty}\frac{r_n-r_{n-1}}{r_{n+1}-r_n}=4.669201609109...\]
其中\(r\)是发生混沌现象时的分界点。上面这个常数叫做Feigenbaum常数,它可能是比圆周率更神秘的常数,我没有做更深入的了解,详情可参见论文《Quantitative universality for a class of nonlinear transformations》,换句话说,混沌演化的过程中存在内部规律性,且这种演化过程存在某种“普适性”。
6.2.6 RNN长依赖学习问题
这一节主要基于对Yoshua Bengio《Learning Long-Term Dependencies with Gradient Descent is Difficult》一文的学习,个人认为它是少有的对长依赖学习做出精彩理论研究和证明的文章。
文章从实验和理论角度证明了:梯度下降算法无法有效学习长依赖(模型在时间t的输出依赖更早时间\(t^{'}\ll t\)时的系统状态)。
一个能学习长依赖的动态系统,至少应该满足以下几个条件:
1、系统能够存储任意时长的信息; 2、系统鲁棒性强,即使对系统输入做随机波动也不影响系统做出正确输出; 3、系统参数可在合理有限的时间内学习到。
- 单节点RNN实验
设计一个满足以上条件的简单的序列二分类问题:
给定任意序列:\(u_1,...,u_T\),二分类器\(C(u_1,...,u_T)\in \{0,1\}\),且分类结果只与序列的前\(L\)(\(L\ll T\))个输入有关,即: \[C(u_1,...,u_T)=C(u_1,...,u_L)\] 显然,\(L\)之后的信息都是噪声(文中实验采用高斯噪声),如果系统不能有效存储任意时长的信息则无法做正确分类。换句话说,分类器内置了一个latching subsystem(暂且翻译为锁存子系统),这个子系统可以提取分类的关键信息,并存储于子系统的状态变量中。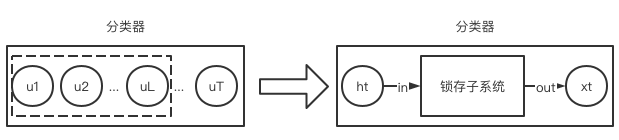
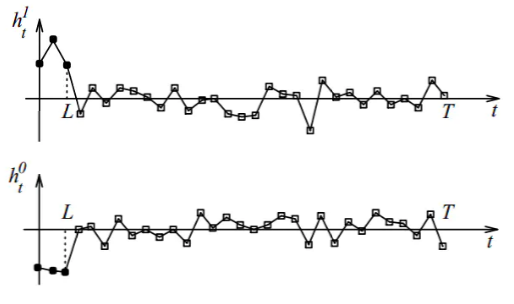
当\(t\leq L\)时,\(h_t\)为可学习调整的参数,当\(L<t\leq T\)时,\(h_t\)为高斯噪声,损失函数为:
\[C=\frac{1}{2}\sum_{p}(x_T^p-d^p)^2\] 其中\(p\)是训练序列的索引,\(d^p\)是目标输出,取值0.8代表分类1,取值-0.8代表分类0,$h_t (t = 1,. . . , L) \(代表抽取了分类关键信息后的计算结果,显然,直接学习\)h_t$要比用原始输入学习 \(h_t(u_t,\theta)\)来的容易,而且不管以上哪种方式,传播误差梯度\(\frac{\partial C}{\partial h_t}\)的方法一样,如果因为梯度消失导致\(h_t\)都学不出来,更别说\(h_t(u_t,\theta)\)了。
以最简单的RNN为例:
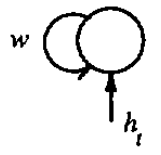
\[ \begin{align*} & y_t^k=f(x_t^k)=tanh(x_t^k) \\ & x_t^k=wf(x_{t-1}^k)+h_t^k \quad t=1...T\\ & x_0^0=x_0^1=1\\ & k \in\{0,1\}\\ \end{align*} \]
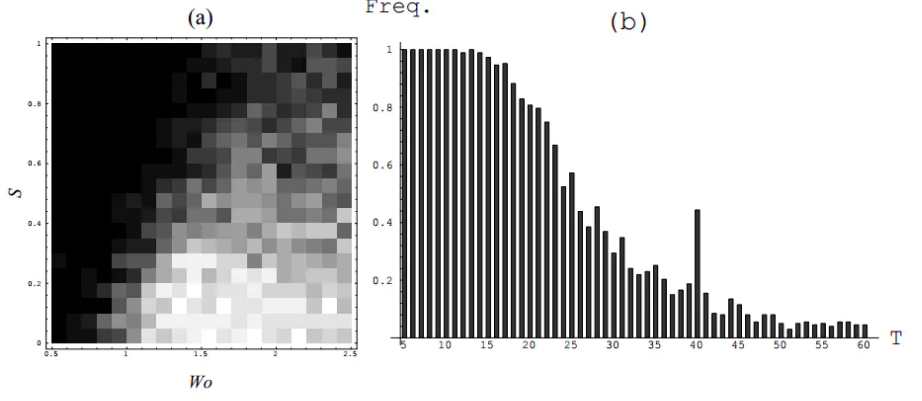
如果\(w>1\),则以上动态系统有两个双曲吸引子,即下图的\((\pm x^*,\pm y^*)\):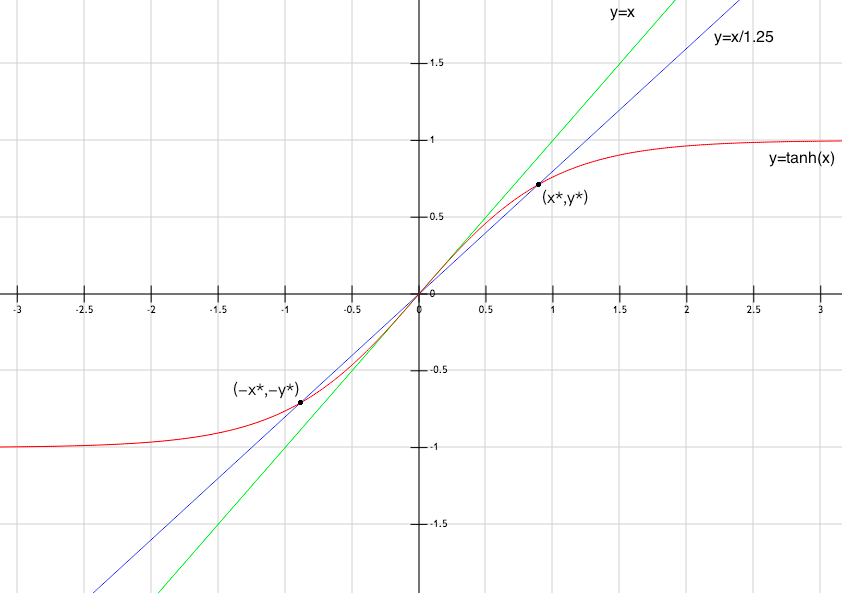
依据《Unified integration of explicit rules and learning by example in recurrent networks》的证明,假设初始状态是\((-x^*,-y^*)\),则存在\(h^*\)使得:
1、如果\(|h_t|<h^*\),\(\forall t\),\(y_t\)的符号可以保持不变,即在负向\((-x^*,-y^*)\)吸引子邻域的点会被吸引;
2、存在有限步数\(L_1\),如果\(h_t>h^*\),\(\forall t \leq L_1\),使得\(y_{L1}>y^*\),即超过\((-x^*,-y^*)\)吸引子邻域的点会被吸引到正向吸引子\((x^*,y^*)\)。
当\(w\)取固定值时,\(L_1\) 随着 \(|h_t|\) 增加而减小。
总结如下:
1、上述简单的系统可以锁存1 bit信息(即输出的符号变化与否);
2、系统通过对一个大的输入保持足够长的时间来存储信息(\(|h_t|>h^*\));
3、对输入做微小的噪声扰动,即使时间很长也不会改变激活函数输出的符号;
4、\(w\)也是可学习的,当\(T\gg L\)时,要求\(w>1\),此时会生成正负向两个吸引子,且\(w\)越大,相应的阈值\(h^*\)越大,因此系统鲁棒性越强。
- 混沌理论角度的解释
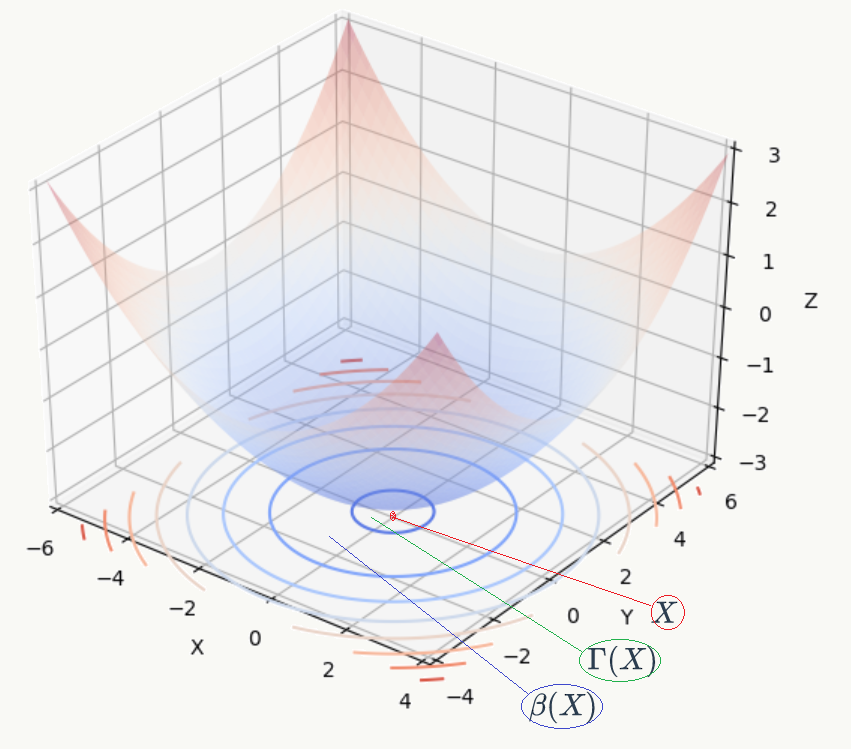
回忆前几节关于映射及吸引子、双曲吸引子的说明,围绕着吸引子(attractor)有几个相关定义:
1、basin of attractor:其实就是吸引子的邻域:
\[\beta(X)=\{p\in \mathbb{R}^m :\forall \epsilon,\exists x \in X s.t.||f(p)-x||<\epsilon \}\]
2、reduced attractor set:其实就是被双曲吸引子强吸引的点集合:
\[\Gamma(X)=\{p\in \mathbb{R}^m :f'(p)的所有特征值都小于1\}\] 直观展示它们的关系如上图,显然:
\[X \subset \Gamma(X) \subset \beta(X) \] 如果任意时刻对一个锁存子系统的输入做微小扰动后都落在该系统双曲吸引子的reduced attractor set中,即图中\(\Gamma(X)\),则该锁存系统具有鲁棒性。
3、对于双曲吸引子\(X\)邻域内的点\(a\),如果在\(\beta(X)\)但不在\(\Gamma(X)\)中,则不确定性会随着\(t\)的增加而呈指数增加,最终微小的扰动会让\(a\)远离\(x\)而进入其他吸引子的邻域,如下图:
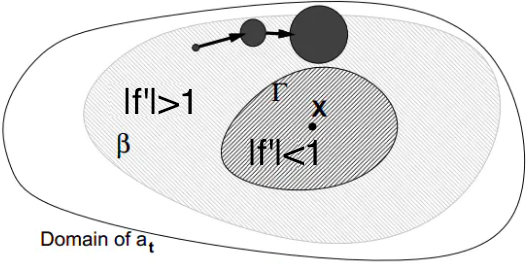
证明:
假设\(\exists u\),满足\(\left\|u\right\|=1\)及\(\left\|f'(x)u\right\|>1\),则根据泰勒展开式,对一个很小的值\(\lambda\)有:
\[f(x+\lambda u)=f(x)+f'(x)\lambda u+O(\left\|\lambda u\right\|^2)\]
对一个开放集合\(U(x)\),存在一个很小的值\(\lambda\),使得\(x+\lambda u \in U(x)\),且\(O(\left\|\lambda u\right\|^2)<\lambda\left\|f'(x)u\right\|-\lambda\)。另\(y=x+\lambda u\),则根据三角不等式有:
\[\left\|-f'(x)\lambda u\right\|-\left\|f(y)-f(x)\right\|<\left\|-f'(x)\lambda u+f(y)-f(x)\right\|\]
而:
\[\left\|-f'(x)\lambda u+f(y)-f(x)\right\|=\left\|O(\left\|\lambda u\right\|^2)\right\|<\lambda\left\|f'(x)u\right\|-\lambda\]
所以有:
\[\lambda \left\|f'(x)u\right\|-\left\|f(y)-f(x)\right\|<\lambda\left\|f'(x)u\right\|-\lambda\]
从而得到:
\[\left\|f(y)-f(x)\right\|>\lambda=\left\|y-x\right\|\]
即:对\(x\)的微小扰动会使得\(f(x)\)的变化“幅度”增大。
4、一个具有鲁棒性的锁存子系统特点是:即使对系统输入有微小扰动,只要每次迭代时\(a_t\)都在双曲吸引子\(X\)的\(\Gamma(X)\)内,则最终会被吸引收敛到双曲吸引子\(X\)附近。如下图:
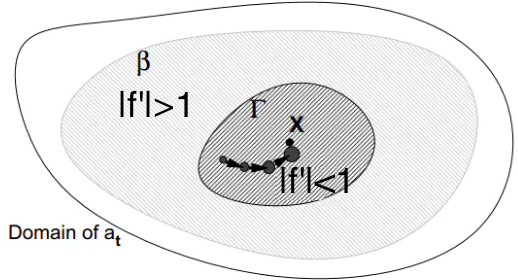
5、动态系统要想做到鲁棒性的锁存信息,则会出现梯度消失现象(gradient vanishing),鱼与熊掌不可兼得。 一个通用的动态系统可以表示为:
\[a_{t}=f(a_{t-1})+x_t,\{a,x\}\in \mathbb{R}^m\]
其中\(a_t\)和\(x_t\)分别是\(t\)时刻系统状态向量和\(t\)时刻外部输入向量,根据导数的定义和双曲吸引子的性质有:
\[|\frac{\partial a_t}{\partial_{a_{t-1}}}|=|f'(a_{t-1})|<1\]
显然,当\(t\rightarrow \infty\)时,\(\frac{\partial a_t}{\partial_{a_{0}}}\rightarrow 0\),梯度消失!
6.3 LSTM
上面两节从原理角度说明了RNN为什么很难学到长依赖,而本节的LSTM是一个伟大的和具有里程碑的模型,最著名的论文是Sepp Hochreiter 与 Jurgen Schmidhuber的《Long Short-Term Memory 》(没错,就是那位怼天怼地怼各种权威的Schmidhuber),从原理上分析解决了RNN学习长依赖中的梯度爆炸(blow up)和梯度消失(vanish)问题,大部分文章只介绍了LSTM的结构,我希望通过本文能抛砖引玉,了解作者为什么这么设计结构。
6.3.1 基本原理
回忆6.1节末的RNN任意两层隐藏层
\[ \delta_{pj}(t-1)=\sum_h^m\delta_{ph}(t)u_{hj}f^{'}(s_{pj}(t-1)) \]
其中:\(h\)是在\(t\)时刻的任何一个隐层节点,\(j\)是在\(t-1\)时刻的任何一个隐层节点,高层的\(\delta\)可以通过循环递归的计算出来,所有\(\delta\)计算完毕后累加求和并应用在\(U\)、\(V\)的权重更新中。
误差从\(t\)时刻的隐藏层\(h\)节点经过任意\(q\)步往\(t-q\)时刻的隐藏层\(j\)节点做反向传播的传播速度如下:
\[ \frac{\partial{\delta_{pj}(t-q)}}{\partial{\delta_{ph}(t)}}=\left\{ \begin{array}{**lr**} f^{'}(s_{pj}(t-1))u_{hj} & q=1 \\ f^{'}(s_{pj}(t-1)) \sum_{i=1}^m \frac{\partial{\delta_{pi}(t-q+1)}}{\partial{\delta_{ph}(t)}}u_{hj} & q>1 \end{array} \right. \]
把上面式子完全展开后得到:
\[ \frac{\partial{\delta_{pj}(t-q)}}{\partial{\delta_{ph}(t)}}=\sum_{i_1=1}^m...\sum_{i_{q-1}=1}^m\prod_{m=1}^qf^{'}(s_{i_m}(t-m))u_{i_mi_{m-1}} \]
大家会发现整个误差反向传播速度是由${m=1}qf{'}(s{i_m}(t-m))u_{i_mi_{m-1}} $决定的:
1、如果\(|f^{'}(s_{i_m}(t-m))u_{i_mi_{m-1}}|>1\),则连乘的结果会随着\(q\)的增加呈指数形式增大,误差反向传播出现梯度爆炸;
2、如果\(|f^{'}(s_{i_m}(t-m))u_{i_mi_{m-1}}|<1\),则连乘的结果会随着\(q\)的增加呈指数形式减小,误差反向传播出现梯度消失。
假设以最简单的RNN为例,即: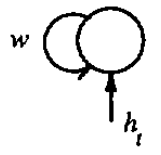
在\(t\)时刻的反向误差传播为:
\[\delta_{h}(t)=\delta_{h}(t+1)u_{hh}f^{'}(s_{h}(t))\] 其中:\(s_{h}(t)=f(net_h(t))\)。要想不出现梯度爆炸或消失,只能满足:
\[u_{hh}f^{'}(s_{h}(t))=1\]
对上式积分下,得到:
\[f(s_{h}(t))=\frac{s_h(t)}{u_{hh}}\]
这意味着,函数\(f\)必须是线性的,显然,当\(u_{hh}=1\)时,有恒等映射函数\(f(x)=x\),上述关系也叫constant error carrousel(CEC),CEC在LSTM的结构设计中举足轻重。
以输入权重为例,由于实际场景中除了自连接节点外,还会有其他输入节点,为简单起见,我们只关注一个额外的输入权重\(w_{ji}\) 。假设通过响应某个输入而开启神经网络单元\(j\),并为了减少总误差,希望它能被长时间激活。显然,对同一个输入权重一方面要存储某些输入范式,一方面又要忽略其他输入范式,而涉及\(j\)节点的函数(上面的CEC)又是线性的,所以对\(w_{ji}\)而言,这些信号会试图让它既得通过开启\(j\)单元对输入做存储又需要防止\(j\)单元被其他输入关闭,这种情况使得学习变得困难。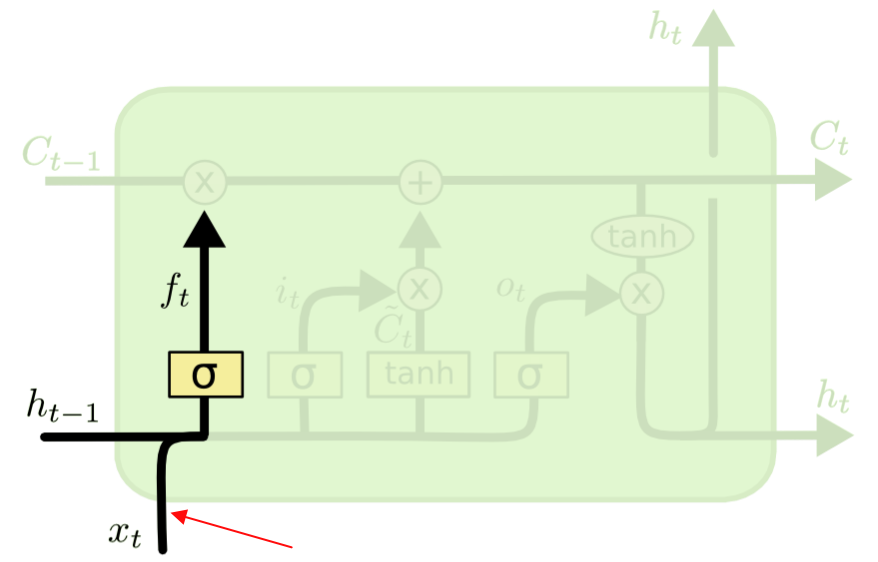
对于输出权重,也存在类似的输出冲突,这里就不在赘述。 为了解决上面的输入和输出冲突,LSTM抽象了1个记忆单元(Memory Cel l)、设计了1个基础结构——遗忘门(Forget Gate)和2个组合结构——输入门(Input Gate)和输出门(Output Gate)来解决冲突。
0、记忆单元是对包含CEC线性单元的抽象,如下图(以RNN作为对比),包含当前时刻输入、上个隐层节点的状态、当前时刻输出、当前时刻隐层节点状态。:
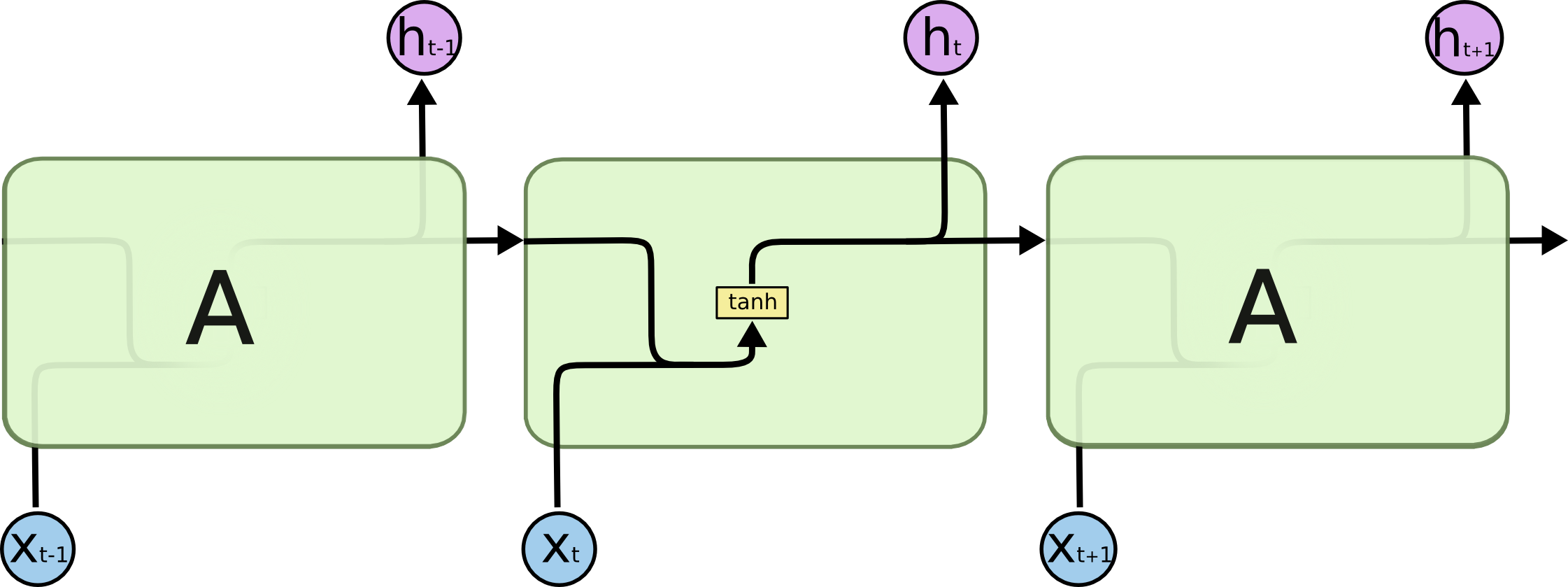
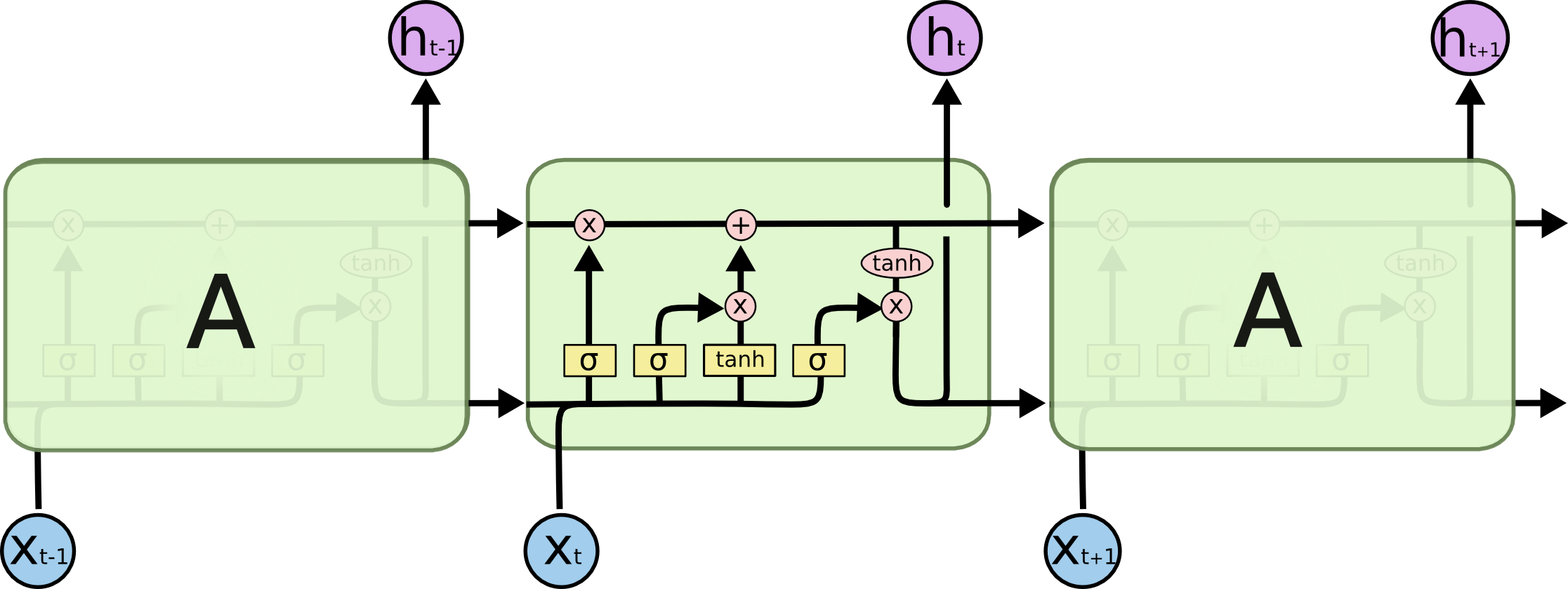
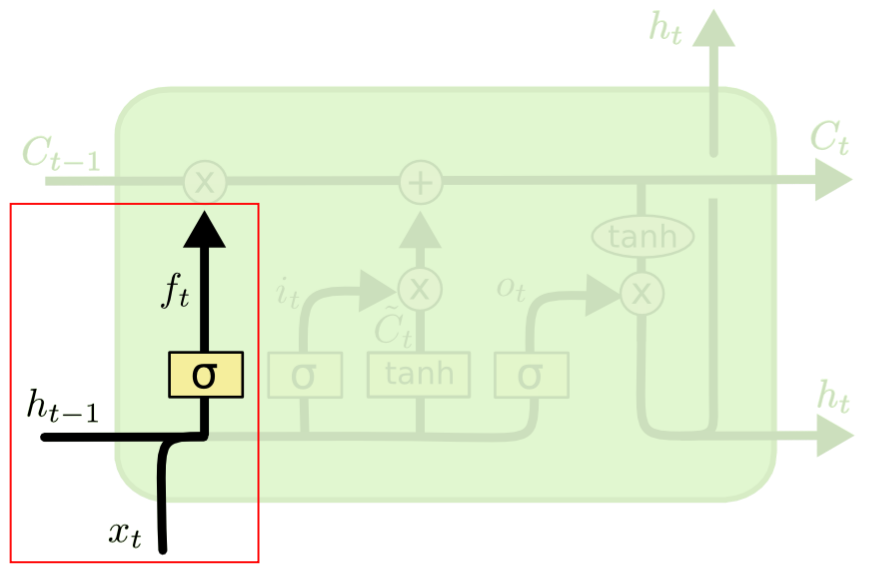
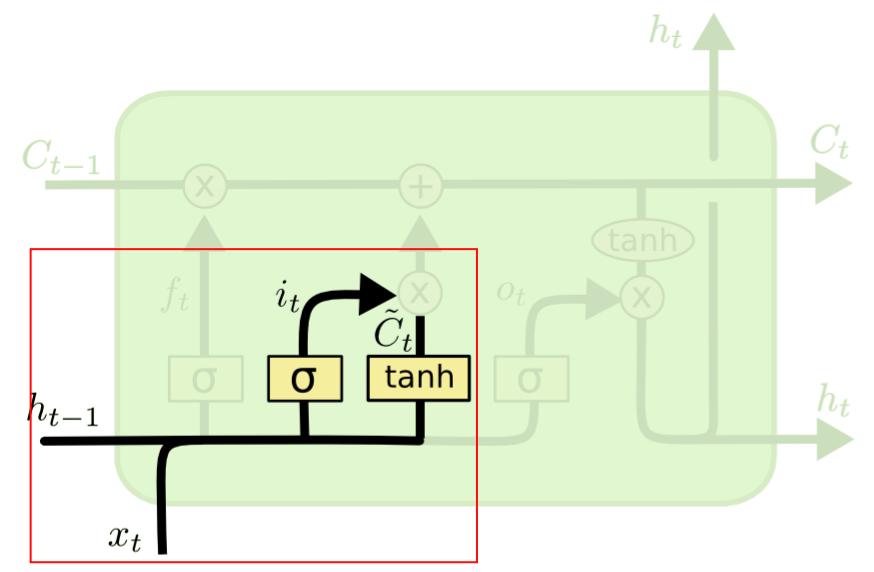
2、输入门的结构如下图:它将上一个隐层的状态\(h_{t-1}\)和当前输入\(x_t\)合并后送入Logistic函数,输出介于0~1之间,同样的,0表示信息不重要,1表示信息重要;同时,\(h_{t-1}\)和\(x_t\)合并后的输入被送入Tanh函数,输出介于-1~1之间,Logistic的输出与Tanh的输出相乘后决定哪些Tanh的输出信息需要保留,哪些要丢掉,也就是说,输入门决定了哪些新的信息要被加进来。
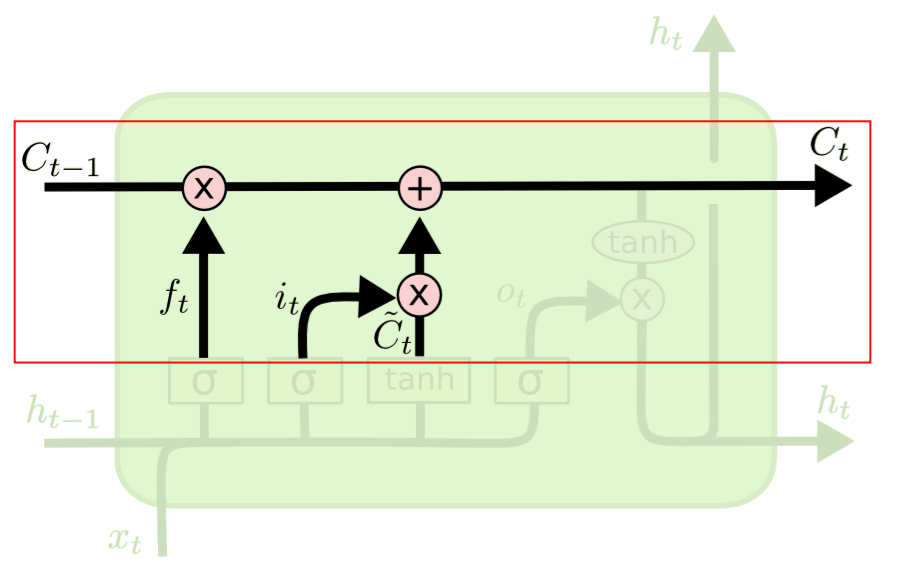
3、输出门的结构如下图:它主要解决隐藏层状态的输出冲突问题,它将上一个隐层的状态\(h_{t-1}\)和当前输入\(x_t\)合并后送入Logistic函数,输出介于0~1之间,然后与当前记忆单元的输出通过Tanh函数变换后的结果相乘,得到当前隐藏层的状态,也就是说,输出门决定了当前隐藏层要携带哪些历史信息,比较好解决了输出冲突。
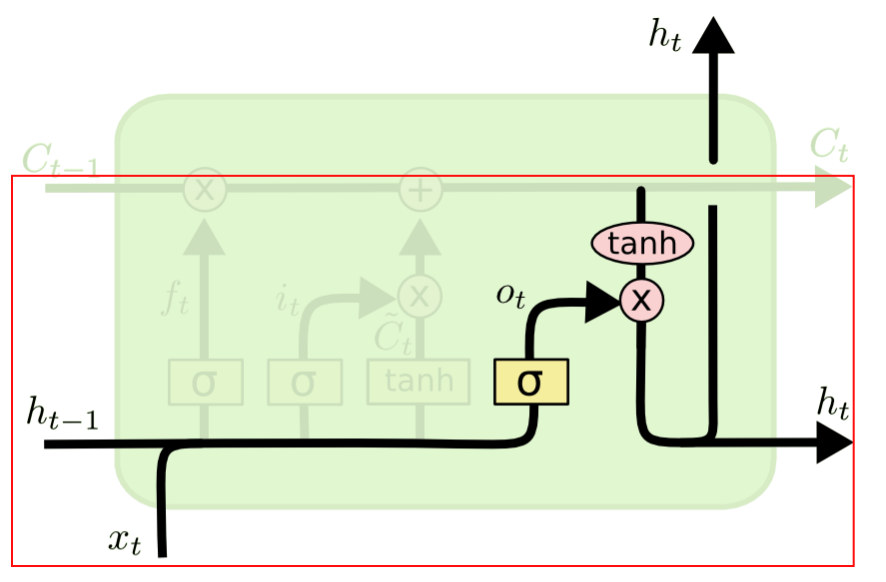
以上图片来源于:《Understanding LSTM Networks》一文,非常不错的一篇LSTM入门文章。后续也有各种各样对经典LSTM的改进(如GRU),但整体上不如LSTM经典(截止2020.10.10在Google Scholar上查寻到该论文已经被引用了37851次,成为20世纪“最火论文”)。
除了比较完美解决了输入输出冲突外,LSTM的计算和存储复杂度并不高,权重更新计算的复杂度为O(W),即与权重总个数线性相关;存储方面也不像使用全流程BPTT的传统方法,要存储大量历史节点信息,LSTM只需要存储一定历史时间步的局部信息。
6.3.2 代码实践
本节以经典的《古诗词生成》为例子,介绍下LSTM的一种应用,以下例子只供娱乐使用。
问题描述如下:
“给定五言绝句的首句,生成整首共4句的五言绝句。”
例如,输入:“月暗竹亭幽,”,输出“月暗竹亭幽,碧昏时尽黄。园春歌雪光,云落分白草。”。
完整代码在:https://github.com/vivounicorn/LstmApp.git,其中,data文件夹里包含了训练好的word2vec模型和迭代了2k+次的模型,可以直接做fine-tune。
1、算法步骤
Step-1:爬取古诗词作为原始数据;
Step-2:清洗原始数据,去掉不符合五言绝句的诗词;
Step-3:准备训练数据和相应的标注;
Step-4:若使用word2vec生成的词向量,则需要生成相关模型;
Step-5:构建以LSTM层和全连接层为主的神经网络;
Step-6:训练和验证模型,并做应用。
2、实现详情
Step-1,爬取古诗词作为原始数据
用开源工具爬取:https://www.gushiwen.org/上的诗句。解析结果的基本格式为:“诗词标题:诗词内容”。
Step-2,数据清洗
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79def _build_base(self,
file_path,
vocab=None,
word2idx=None,
idx2word=None) -> None:
"""
To scan the file and build vocabulary and so on.
:param file_path: the file path of poetic corpus, one poem per line.
:param vocab: the vocabulary.
:param word2idx: the mapping of word to index.
:param idx2word: the mapping of index to word
:return: None.
"""
# 去掉无关字符
pattern = re.compile(u"_|\(|(|《")
with open(file_path, "r", encoding='UTF-8') as f:
for line in f:
try:
line = line.strip(u'\n')
title, content = line.strip(SPACE).split(u':')
content = content.replace(SPACE, u'')
idx = re.search(pattern, content)
if idx is not None:
content = content[:idx.span()[0]]
# 把指定长度的诗词选出来,如:五言绝句。
if len(content) < self.embedding_input_length: # Filter data according to embedding input
# length to improve accuracy.
continue
words = []
for i in range(0, len(content)):
word = content[i:i + 1]
if (i + 1) % self.embedding_input_length == 0 and word not in [',', ',', ',', '.', '。']:
words = []
break
words.append(word)
self.all_words.append(word)
if len(words) > 0:
self.poetrys.append(words)
except Exception as e:
log.error(str(e))
# 生成词汇表,保留出现频次top n的字
if vocab is None:
top_n = Counter(self.all_words).most_common(self.vocab_size - 1)
top_n.append(SPACE)
self.vocab = sorted(set([i[0] for i in top_n]))
else:
top_n = list(vocab)[:self.vocab_size - 1]
top_n.append(SPACE)
self.vocab = sorted(set([i for i in top_n])) # cut vocab with threshold.
log.debug(self.vocab)
# 生成“字”到“编号”的映射,把每个字做了唯一编号,“空格”也做编号
if word2idx is None:
self.word2idx = dict((c, i) for i, c in enumerate(self.vocab))
else:
self.word2idx = word2idx
# 生成“编号”到“字”的映射
if idx2word is None:
self.idx2word = dict((i, c) for i, c in enumerate(self.vocab))
else:
self.idx2word = idx2word
# Function of mapping word to index.
# 以 “字” 查找 “编号”的函数,没在词汇表的“字”用“空格”的编号代替
self.w2i = lambda word: self.word2idx.get(str(word)) if self.word2idx.get(word) is not None \
else self.word2idx.get(SPACE)
# Function of mapping index to word.
# 以 “编号”查找 “字” 的函数,找不到的“字”用“空格”代替
self.i2w = lambda idx: self.idx2word.get(int(idx)) if self.idx2word.get(int(idx)) is not None \
else SPACE
# Full vectors.
# 把文本表示的诗词变成由“编号”表示的向量,如:“床前明月光,”变成[1,2,3,4,5,6]
self.poetrys_vector = [list(map(self.w2i, poetry)) for poetry in self.poetrys]
self._data_size = len(self.poetrys_vector)
self._data_index = np.arange(self._data_size)Step-3:准备训练数据
原理是:根据指定的输入长度(input length)截取序列并生成特征数据,指定这个序列的下一个字为“标注”。
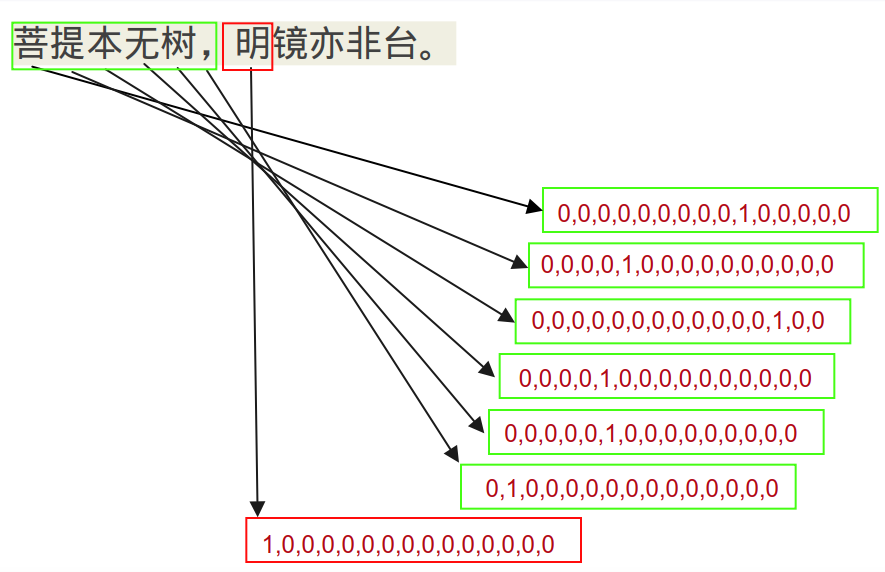
例如:“菩提本无树,明镜亦非台。”,以五言绝句为例,输入长度为6(包括标点符号),可以生成以下样本:
特征 标注 菩提本无树, 明 提本无树,明 镜 本无树,明镜 亦 无树,明镜亦 非 树,明镜亦非 台 ,明镜亦非台 。 对每个字,支持两种编码方式:基于词汇表的one hot和基于语义distributed representation的word2vec。
1、One-hot
假设输入长度为6,词汇表维度为8000,则,对于一个样本有:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41def _one_hot_encoding(self, sample):
"""
One-hot encoding for a sample, a sample will be split into multiple samples.
:param sample: a sample. [1257, 6219, 3946]
:return: feature and label. feature:[[0,0,0,1,0,0,......],
[0,0,0,0,0,1,......],
[1,0,0,0,0,0,......]];
label: [0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0......]
"""
if type(sample) != list or 0 == len(sample):
log.error("type or length of sample is invalid.")
return None, None
feature_samples = []
label_samples = []
idx = 0
# embedding_input_length即为输入窗口长度,五言绝句为6,当然也可以取其他值,但会影响训练精度和时间。
while idx < len(sample) - self.embedding_input_length:
feature = sample[idx: idx + self.embedding_input_length]
label = sample[idx + self.embedding_input_length]
label_vector = np.zeros(
shape=(1, self.vocab_size),
dtype=np.float
)
# 序列的下一个字为标注
label_vector[0, label] = 1.0
feature_vector = np.zeros(
shape=(1, self.embedding_input_length, self.vocab_size),
dtype=np.float
)
# 根据词汇表,相应的编号赋值为1,其余都是0.
for i, f in enumerate(feature):
feature_vector[0, i, f] = 1.0
idx += 1
feature_samples.append(feature_vector)
label_samples.append(label_vector)
return feature_samples, label_samples特征矩阵为:1×68000 标注向量为:18000
![]()
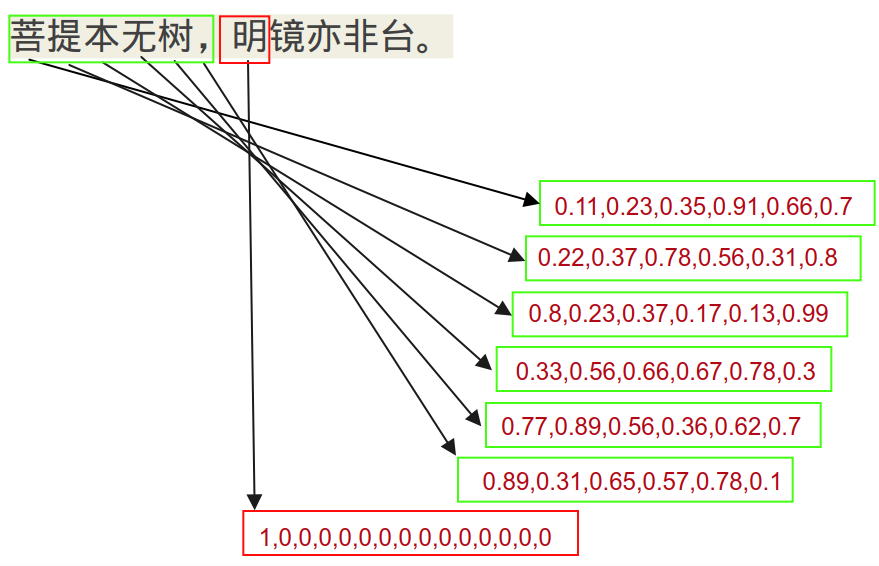
2、Word2vec
假设输入长度为6,词的语义向量维度为200,则,对于一个样本有:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44def _word2vec_encoding(self, sample):
"""
word2vec encoding for sample, a sample will be split into multiple samples.
:param sample: a sample. [1257, 6219, 3946]
:return: feature and label.feature:[[0.01,0.23,0.05,0.1,0.33,0.25,......],
[0.23,0.45,0.66,0.32,0.11,1.03,......],
[1.22,0.99,0.68,0.7,0.8,0.001,......]];
label: [0,0,0,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0......]
"""
if type(sample) != list or 0 == len(sample):
log.error("type or length of sample is invalid.")
return None, None
feature_samples = []
label_samples = []
idx = 0
while idx < len(sample) - self.embedding_input_length:
feature = sample[idx: idx + self.embedding_input_length]
label = sample[idx + self.embedding_input_length]
if self.w2v_model is None:
log.error("word2vec model is none.")
return None, None
label_vector = np.zeros(
shape=(1, self.vocab_size),
dtype=np.float
)
# 序列的下一个字为标注
label_vector[0, label] = 1.0
feature_vector = np.zeros(
shape=(1, self.embedding_input_length, self.w2v_model.size),
dtype=np.float
)
# 用训练好的word2vec模型获取相应“字”的语义向量
for i in range(self.embedding_input_length):
feature_vector[0, i] = self.w2v_model.get_vector(feature[i])
idx += 1
feature_samples.append(feature_vector)
label_samples.append(label_vector)
return feature_samples, label_samples特征矩阵为:1×6200 标注向量为:18000
![]()
Step-4:基于word2vec训练词向量
使用dump函数将训练数据相关数据结构dump下来,其中poetrys_words.dat文件可直接作为word2vec的训练数据(注:要训练的是字粒度的语义向量),文件内容类似这样,一行一首诗,字与字空格分割:
寒 随 穷 律 变 , 春 逐 鸟 声 开 。 初 风 飘 带 柳 , 晚 雪 间 花 梅 。 碧 林 青 旧 竹 , 绿 沼 翠 新 苔 。 芝 田 初 雁 去 , 绮 树 巧 莺 来 。 晚 霞 聊 自 怡 , 初 晴 弥 可 喜 。 日 晃 百 花 色 , 风 动 千 林 翠 。 池 鱼 跃 不 同 , 园 鸟 声 还 异 。 寄 言 博 通 者 , 知 予 物 外 志 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def dump_data(self) -> None:
"""
To dump: poetry's words list, poetry's words vectors, poetry's words vectors for training,
poetry's words vectors for testing, poetry's words vectors for validation,
poetry's words vocabulary, poetry's word to index mapping,poetry's index to word mapping.
:return: None
"""
org_filename = self.dump_dir + 'poetrys_words.dat'
self._dump_list(org_filename, self.poetrys)
vec_filename = self.dump_dir + 'poetrys_words_vector.dat'
self._dump_list(vec_filename, self.poetrys_vector)
train_vec_filename = self.dump_dir + 'poetrys_words_train_vector.dat'
self._dump_list(train_vec_filename, self.poetrys_vector_train)
valid_vec_filename = self.dump_dir + 'poetrys_words_valid_vector.dat'
self._dump_list(valid_vec_filename, self.poetrys_vector_valid)
test_vec_filename = self.dump_dir + 'poetrys_words_test_vector.dat'
self._dump_list(test_vec_filename, self.poetrys_vector_test)
vocab_filename = self.dump_dir + 'poetrys_vocab.dat'
self._dump_list(vocab_filename, list(self.vocab))
w2i_filename = self.dump_dir + 'poetrys_word2index.dat'
self._dump_dict(w2i_filename, self.word2idx)
i2w_filename = self.dump_dir + 'poetrys_index2word.dat'
self._dump_dict(i2w_filename, self.idx2word)模型方面直接使用gensim包,定义如下,根据参数不同,可以训练得到基于CBOW或SkipGram的语义向量,我们这种规模下,本质上没有太大差别,我们这里使用SkipGram。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import gensim
from gensim.models import Word2Vec
from gensim.models.word2vec import LineSentence
import multiprocessing
import numpy as np
from src.config import Config
from src.utils import Logger
class Word2vecModel(object):
"""
Word2vec model class.
"""
def __init__(self,
cfg_path='/home/zhanglei/Gitlab/LstmApp/config/cfg.ini',
is_ns=False):
"""
To initialize model.
:param cfg_path: he path of configration file.
:param model_type:
"""
cfg = Config(cfg_path)
global log
log = Logger(cfg.model_log_path())
self.model = None
self.is_ns = is_ns
self.vec_out = cfg.vec_out()
self.corpus_file = cfg.corpus_file()
self.window = cfg.window()
self.size = cfg.size()
self.sg = cfg.sg()
self.hs = cfg.hs()
self.negative = cfg.negative()
def train_vec(self) -> None:
"""
To train a word2vec model.
:return: None
"""
output_model = self.vec_out + 'w2v_size{0}_sg{1}_hs{2}_ns{3}.model'.format(self.size,
self.sg,
self.hs,
self.negative)
output_vector = self.vec_out + 'w2v_size{0}_sg{1}_hs{2}_ns{3}.vector'.format(self.size,
self.sg,
self.hs,
self.negative)
# 是否做负采样
if not self.is_ns:
self.model = Word2Vec(LineSentence(self.corpus_file),
size=self.size,
window=self.window,
sg=self.sg,
hs=self.hs,
workers=multiprocessing.cpu_count())
else:
self.model = Word2Vec(LineSentence(self.corpus_file),
size=self.size,
window=self.window,
sg=self.sg,
hs=self.hs,
negative=self.negative,
workers=multiprocessing.cpu_count())
self.model.save(output_model)
self.model.wv.save_word2vec_format(output_vector, binary=False)
def load(self, path):
"""
To load a word2vec model.
:param path: the model file path.
:return: success True otherwise False.
"""
try:
self.model = gensim.models.Word2Vec.load(path)
return True
except:
return False
def most_similar(self, word):
"""
Return the most similar words.
:param word: a word.
:return: similar word list.
"""
word = self.model.most_similar(word)
for text in word:
log.info("word:{0} similar:{1}".format(text[0], text[1]))
return word
# 获取某个字 的语义向量
def get_vector(self, word):
"""
To get a word's vector.
:param word: a word.
:return: word's word2vec vector.
"""
try:
return self.model.wv.get_vector(str(word))
except KeyError:
return np.zeros(
shape=(self.size,),
dtype=np.float
)
# 也可以直接把keras的embedding层给拿出来,
# 为了直观,我这里没有直接用它,如果要用,记着把语义向量的权重冻结下。
def get_embedding_layer(self, train_embeddings=False):
"""
To get keras embedding layer from model.
:param train_embeddings: if frozen the layer.
:return: embedding layer.
"""
try:
return self.model.wv.get_keras_embedding(train_embeddings)
except KeyError:
return NoneStep-5:构建LSTM模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49def _build(self,
lstm_layers_num,
dense_layers_num):
"""
To build a lstm model with lstm layers and densse layers.
:param lstm_layers_num: The number of lstm layers.
:param dense_layers_num:The number of dense layers.
:return: model.
"""
units = 256
model = Sequential()
# 样本特征向量的维度,onehot为词汇表大小,word2vec为语义向量维度
if self.mode == WORD2VEC:
dim = self.data_sets.w2v_model.size
elif self.mode == ONE_HOT:
dim = self.vocab_size
else:
raise ValueError("mode must be word2vec or one-hot.")
# embedding_input_length为输入序列窗口大小,如:五言绝句取为6
model.add(Input(shape=(self.embedding_input_length, dim)))
# 可以加多个LSTM层提取序列特征,这里会把之前每隔时刻的隐层都输出出来
for i in range(lstm_layers_num - 1):
model.add(LSTM(units=units * (i + 1),
return_sequences=True))
model.add(Dropout(0.6))
# 注意这里我只要最后一个隐层的输出
model.add(LSTM(units=units * lstm_layers_num,
return_sequences=False))
model.add(Dropout(0.6))
# 可以加多个稠密层,用于对之前提取出来特征的组合
for i in range(dense_layers_num - 1):
model.add(Dense(units=units * (i + 1)))
model.add(Dropout(0.6))
# 最后一层,用softmax做分类
model.add(Dense(units=self.vocab_size,
activation='softmax'))
# 使用交叉熵损失函数,优化器选择默认参数的adam(ps:随便选的,没做调参)
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model.summary()
# 可视化输出模型结构
plot_model(model, to_file='../model.png', show_shapes=True, expand_nested=True)
self.model = model
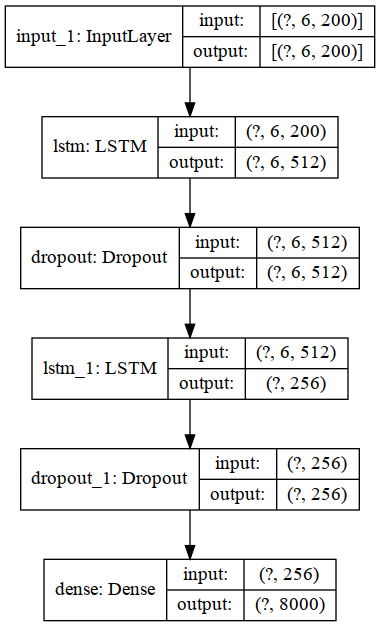
return model例如:使用200维语义向量、输入长度6、词汇量8000、两层LSTM,一层Dense的模型结构如下:
![]()
Step-6:模型训练和应用
1 | #!/usr/bin/env python3 |
在model.log里会看到训练时的中间信息,如下,随着迭代次数变多,效果会越来越好,包括标点符号的规律也会学进去:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
[2020-11-05 12:58:48,723] - lstm_model.py [Line:127] - [DEBUG]-[thread:140045784893248]-[process:29513] - begin training
[2020-11-05 12:58:48,723] - lstm_model.py [Line:132] - [DEBUG]-[thread:140045784893248]-[process:29513] - batch_size:32,steps_per_epoch:355,epochs:5000,validation_steps152
[2020-11-05 12:59:10,260] - lstm_model.py [Line:194] - [INFO]-[thread:140045784893248]-[process:29513] - ==================Epoch 0, Loss 7.93123197555542=====================
[2020-11-05 12:59:11,968] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 欲别牵郎衣,粳酗蓦釱北,鈒静槃遍衫。恸阳日搦蛆,
[2020-11-05 12:59:12,816] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 金庭仙树枝,莨行查娇乂。具撅日霈韂,帝鸟 维。。
[2020-11-05 12:59:13,659] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 素艳拥行舟,母 佶翕何,藁澡 。一 钺辗。,
[2020-11-05 12:59:14,494] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 白鹭拳一足,芾 乡诏秩,启窑 展赢,酪溜劫騊 ,
[2020-11-05 12:59:15,385] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 恩酬期必报,闾瞢,颾钏。啾,。耴望,薖,州耒朿。
[2020-11-05 12:59:16,277] - lstm_model.py [Line:197] - [INFO]-[thread:140045784893248]-[process:29513] - 君去方为宰,沈乡看一帷,柳跂 仁柳,营空长日韍。
[2020-11-05 12:59:16,278] - lstm_model.py [Line:198] - [INFO]-[thread:140045784893248]-[process:29513] - ==================End=====================
......
[2020-11-06 02:12:12,971] - lstm_model.py [Line:194] - [INFO]-[thread:140348029687616]-[process:31309] - ==================Epoch 2106, Loss 7.458868980407715=====================
[2020-11-06 02:12:13,732] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 新开窗犹偏,回雨草花天。谁因家群应,人年功日未。
[2020-11-06 02:12:14,498] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 此心非一事,白物郡期旧。相爱含将回,更相日见光。
[2020-11-06 02:12:15,274] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 刻舟寻已化,有恨多两开。去闻难乱东,地中当如来。
[2020-11-06 02:12:16,069] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 带水摘禾穗,鸟独光冥客。拂船不自已,远年必年非。
[2020-11-06 02:12:16,846] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 茕茕孤思逼,此前路去地。如事别自以,闻阳近高酒。
[2020-11-06 02:12:17,613] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 西陆蝉声唱,日衣烟东云。春出不饥家,马白贵风御。
[2020-11-06 02:12:17,614] - lstm_model.py [Line:198] - [INFO]-[thread:140348029687616]-[process:31309] - ==================End=====================
[2020-11-06 02:13:56,069] - lstm_model.py [Line:194] - [INFO]-[thread:140348029687616]-[process:31309] - ==================Epoch 2112, Loss 7.728175163269043=====================
[2020-11-06 02:13:56,946] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 旅泊多年岁,发知期东今。君自舟岁未,应当折君新。
[2020-11-06 02:13:57,731] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 吾师师子儿,花其重前相。鸟千人身一,清相无道因。
[2020-11-06 02:13:58,532] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 和吹度穹旻,此外更高可。来闻人成独,故去深看春。
[2020-11-06 02:13:59,317] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 下直遇春日,独与时相飞。江君贤犹名,清清曲河人。
[2020-11-06 02:14:00,089] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 月暗竹亭幽,碧昏时尽黄。园春歌雪光,云落分白草。
[2020-11-06 02:14:00,861] - lstm_model.py [Line:197] - [INFO]-[thread:140348029687616]-[process:31309] - 睢阳陷虏日,远平然多岩。公水三共朝,月看同出人。
[2020-11-06 02:14:00,861] - lstm_model.py [Line:198] - [INFO]-[thread:140348029687616]-[process:31309] - ==================End=====================
[2020-11-06 02:15:22,836] - lstm_model.py [Line:148] - [DEBUG]-[thread:140348029687616]-[process:31309] - end training
6.4 Attention机制
6.4.1 什么是Attention机制
在人类的认知过程中,Attention(注意力)是所有感知和认知操作的一种核心属性。由于人类对多来源信息的处理能力有限,Attention机制可以帮助我们选择、调整并聚焦在那些与当前目标行为最相关的的信息上。就像小学生上课,主要行为需要集中在黑板和老师身上,但周围的同学、环境等信息也会涌入大脑并参与竞争,所以集中注意力是成为好学生的必要条件之一。
再比如计算机视觉应用中,Attention机制和感受野类似,都是对人类真实行为的抽象模拟,人类观察事物时,依据自己当时的兴趣点,“天然”会关注“重点”同时忽略无关点,而重点也一定是一些局部信息,不同的人如果关注的“重点”相同,一定程度上就是“臭味相投”。
当然,Attention机制也可以看作是一种通用框架,逻辑类似第三章中讲的的统一框架,夸张点说它也是某种“上帝视角”,目前它在:计算机视觉(如:图像检测、识别、跟踪等)、自然语言处理(如:翻译、问答、摘要等)、计算机视觉与自然语言处理交叉领域(如:根据图像生成文本描述等)、算法任务(如:神经图灵机)、机器人应用(如:人机交互、控制、导航)等领域的研究和应用遍地开花。
6.4.2 从Seq2Seq模型说起
Sequence-to-sequence模型是一种典型的DNN模型,被广泛应用于处理序列问题,如:机器翻译、内容生成等,最早在《Sequence to Sequence Learning with Neural Networks》一文中被提出,以及更早一些具有类似思想,基于RNN Encoder-Decoder做机器翻译的《Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation》。 seq2seq问题处理过程类似这样:

以机器翻译:“我是中国人”\(\Rightarrow\)“I am from china”为例,如果Seq2seq模型采用Encoder-Decoder框架,那么处理过程类似这样:

其中:
1、\(x\)为源输入,像这里的“我是中国人”,进入Encoder模块前一般会被表示为一个语义向量<\(x_1,x_2,...,x_n\)>(如:利用word2vec做word embedding进而生成隐语义向量);
2、接着,Encoder模块负责接收输入序列并将其抽象/压缩/提取/编码输出为一个上下文向量,这个向量隐含了源输入的序列/语义等各种信息,即执行:\(Context=E(x_1,x_2,...,x_n)\);
3、上下文向量做为输入进入Decoder模块,并由Decoder模块生成最终的目标序列\(y\),即执行:\(y_i=D(Context,y_1,y_2,...,y_{i-1})\)。
假设: 1、“我是中国人”被表示为以下向量:
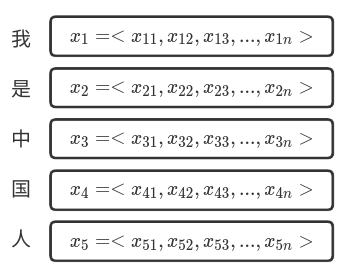
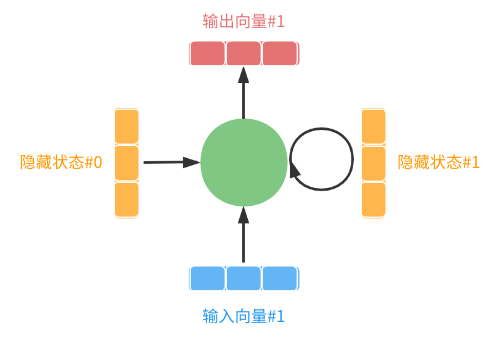
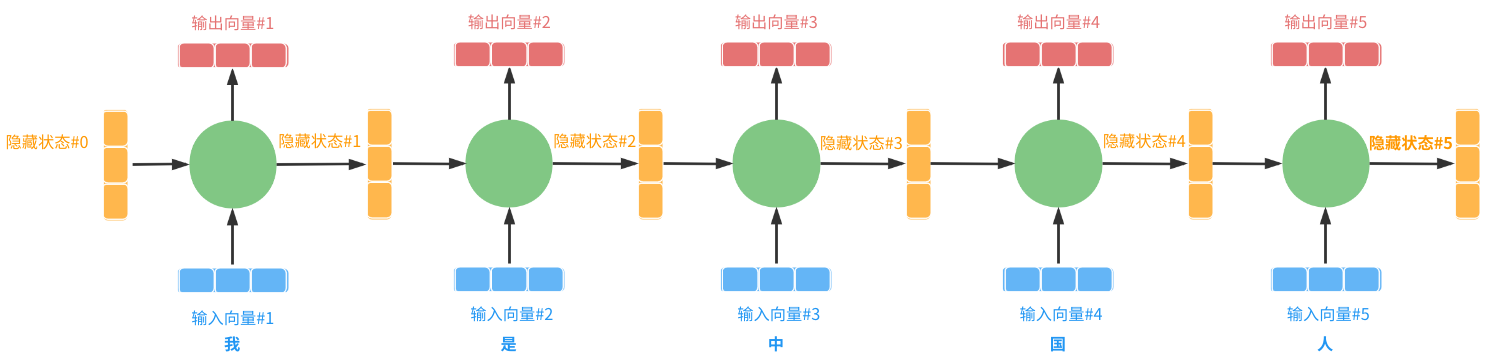

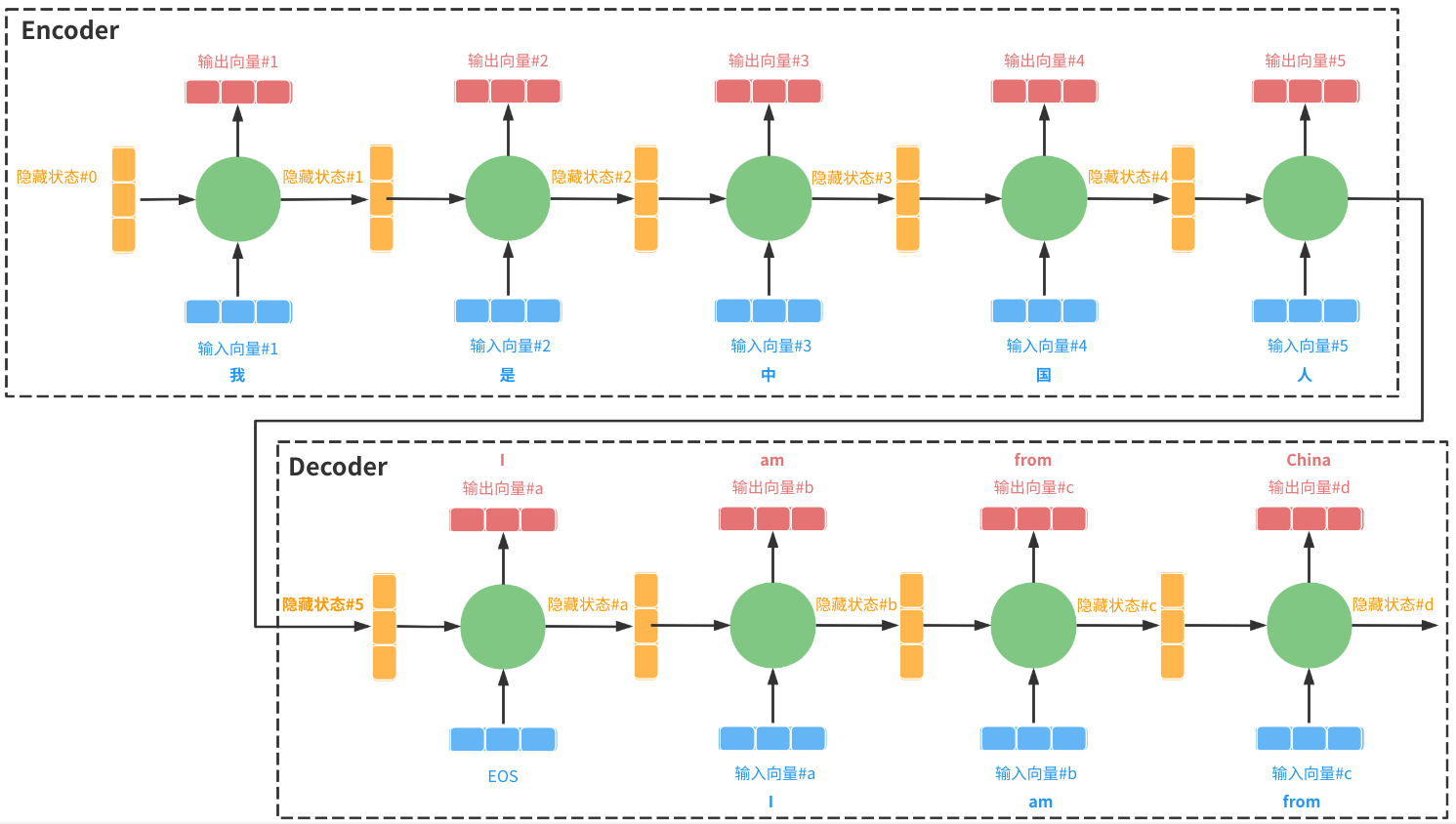
即:
\(y_1=D(隐藏状态\#5)\) = I
\(y_2=D(隐藏状态\#5,y_1)\) = am
\(y_3=D(隐藏状态\#5,y_1,y_2)\) = from
\(y_4=D(隐藏状态\#5,y_1,y_2,y_3)\) = China
在没有Attention机制作用时,生成过程使用的是 相同 的上下文向量:“隐藏状态#5”,即,输入序列“我是中国人”中的每个字对翻译结果为“I am from China”的每个单词的贡献是一样的,这显然是不合理的(比如:“是”对China的贡献要远低于“中”和“国”)。为解决此缺点,引入Attention机制,如下: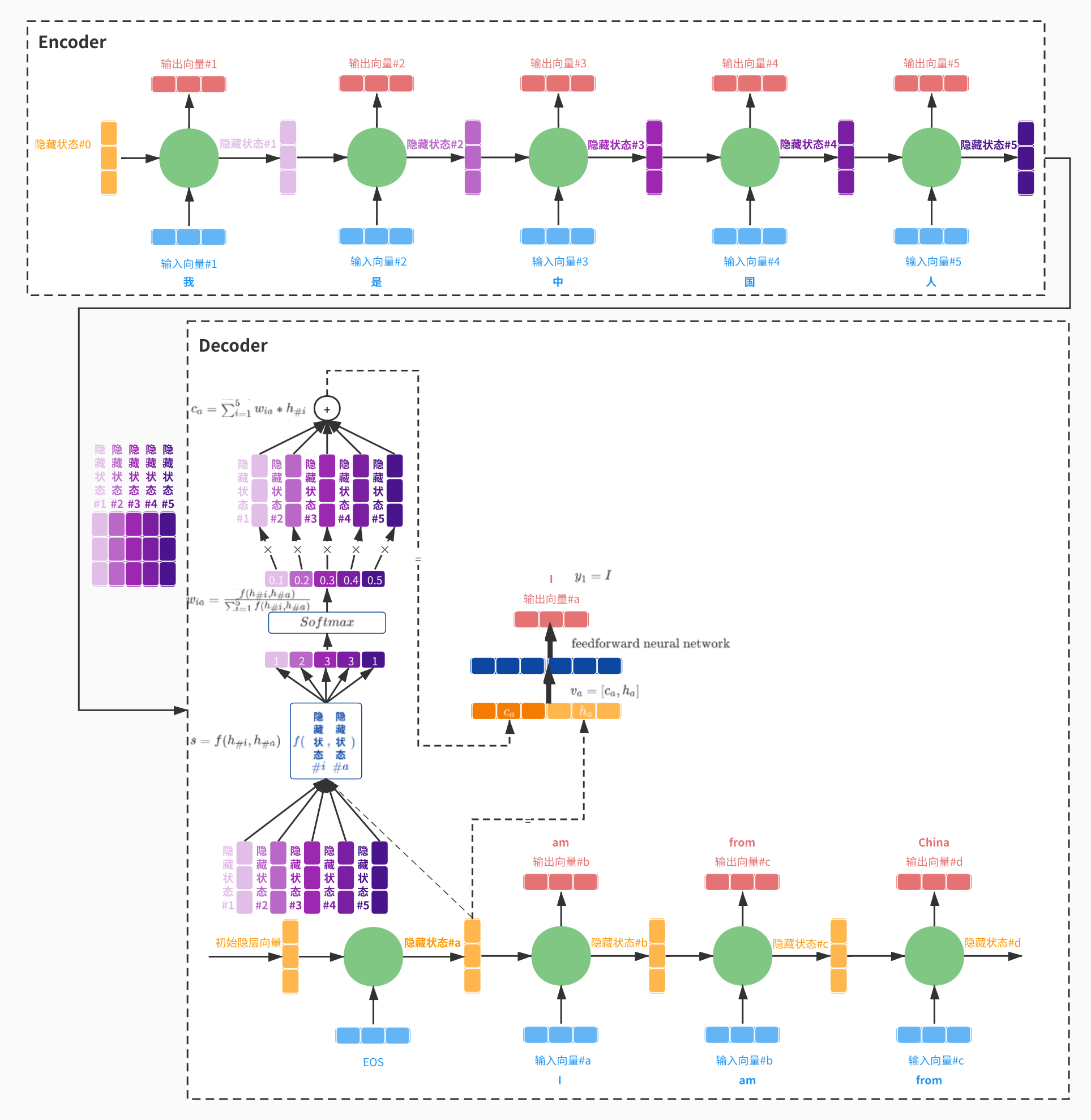
- Encoder阶段,从原来只保留最后一次迭代的隐层向量,改为保留每次迭代的隐层向量,每个隐层向量隐含了相应输入向量的语义信息;
- 以上所有隐层向量传入Decoder阶段;
- 以Decoder阶段RNN的第一次迭代为例:
1、输入为一个“初始向量”和embedding后的“EOS”(输入结束标识符)向量;
2、第一次迭代产生隐层向量#a;
3、依据函数\(f\),每个Encoder阶段传来的隐层向量(#1,#2,...,#5)分别和隐层向量#a计算得分: \[s=f(h_{\#i},h_{\#a})\]
4、计算出的得分利用Softmax函数做归一化: \[w_{ia}=\frac{f(h_{\#i},h_{\#a})}{\sum_{i=1}^{n=5}f(h_{\#i},h_{\#a})}\]
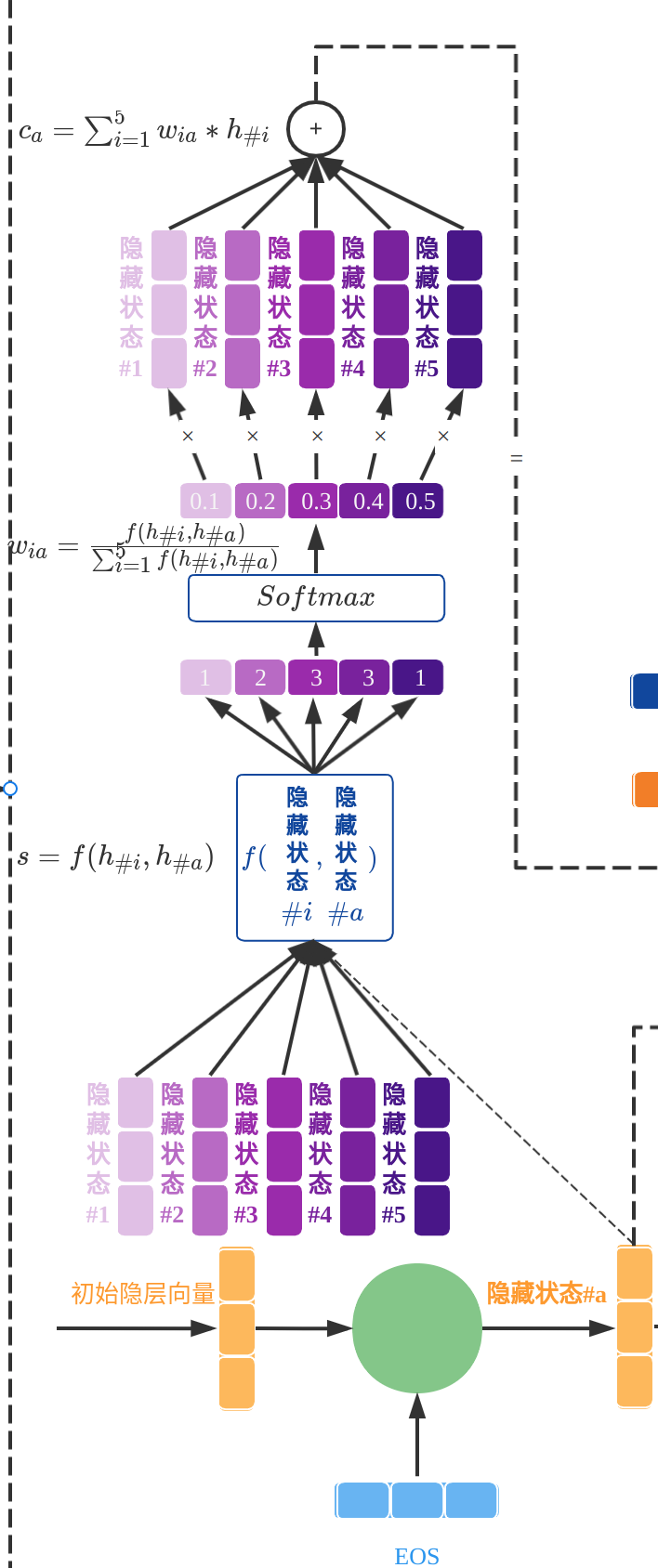
5、用上面计算出的权重对:隐层向量(#1,#2,...,#5)做加权求和,得到当前迭代的上下文向量: \[c_{a}=\sum_{i=1}^{n=5}w_{ia}*h_{\#i}\]
6、拼接新的上下文向量\(c_a\)与当前隐层向量\(h_{\#a}\),得到: \[v_a=[c_a,h_{\#a}]\]
7、将上述向量送入一个前馈神经网络,注意,训练时此网络和整个RNN网络是联合训练的;
8、以上网络的输出向量即为目标内容:\(y_1=I\),其他迭代过程类似就不再赘述。
1、训练数据
1)、下载数据集
下载:http://www.manythings.org/anki/cmn-eng.zip 数据集,内容类似这样:
1 | I received an invitation. 我收到了一张请帖。 CC-BY 2.0 (France) Attribution: tatoeba.org #258705 (CK) & #332420 (fucongcong) |
2)、安装繁简转换器
由于训练集是繁体的,所以需要做下繁简转换,我这里使用OpenCC库:https://github.com/BYVoid/OpenCC 通常情况使用以下命令可安装:
1 | pip install opencc |
使用方法如下:
1 | import opencc |
但如果无法成功,尤其在ubuntu 18.04下,也可以尝试源码安装,不过编译过程很痛苦,你可能会遇到各种各样稀奇古怪的错误,最简单的方案是使用以下项目:https://pypi.org/project/opencc-python-reimplemented/
1 | pip install opencc-python-reimplemented |
使用方法如下:
1 | import opencc |
3)、安装matplotlib字体 由于默认matplotlib不支持显示中文,会报错:
1 | RuntimeWarning: Glyph ***** missing from current font. font.set_text(s, 0.0, flags=flags) |
网上有一堆所谓解决办法,但真正靠谱的没几种,不想尝试的可以用我下面的方法,该方法适用于:deepin及ubuntu 18.04。
下载中文字体,如:SimHei(https://github.com/StellarCN/scp_zh/blob/master/fonts/SimHei.ttf)
在终端查看matplotlib路径
1 | import matplotlib |
例如输出:
/home/leon/.local/lib/python3.8/site-packages/matplotlib/mpl-data/matplotlibrc
进入目录:
/home/leon/.local/lib/python3.8/site-packages/matplotlib/mpl-data/fonts/ttf
把上面的字体放入该目录后,删除缓存文件:
1 | import matplotlib |
例如输出:
/home/leon/.cache/matplotlib
执行:
rm -rf /home/leon/.cache/matplotlib
- 修改matplotlibrc配置文件
例如路径:
/home/leon/.local/lib/python3.8/site-packages/matplotlib/mpl-data/matplotlibrc 改三个部分如下:
1 | #small, medium, large, x-large, xx-large, larger, or smaller |
2、数据预处理
1 | import opencc |
3、实现Encoder编码器
1 | import tensorflow as tf |
4、实现Decoder解码器
BahdanauAttention
Bahdanau在《Neural Machine Translation by Jointly Learning to Align and Translate》这篇论文提出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30import tensorflow as tf
class BahdanauAttention(tf.keras.layers.Layer):
def __init__(self, units):
super(BahdanauAttention, self).__init__()
self.W1 = tf.keras.layers.Dense(units)
self.W2 = tf.keras.layers.Dense(units)
self.V = tf.keras.layers.Dense(1)
def call(self, query, values):
# 隐藏层的形状 == (批大小,隐藏层大小)
# hidden_with_time_axis 的形状 == (批大小,1,隐藏层大小)
# 这样做是为了执行加法以计算分数
hidden_with_time_axis = tf.expand_dims(query, 1)
# 分数的形状 == (批大小,最大长度,1)
# 我们在最后一个轴上得到 1, 因为我们把分数应用于 self.V
# 在应用 self.V 之前,张量的形状是(批大小,最大长度,单位)
score = self.V(tf.nn.tanh(
self.W1(values) + self.W2(hidden_with_time_axis)))
# 注意力权重 (attention_weights) 的形状 == (批大小,最大长度,1)
attention_weights = tf.nn.softmax(score, axis=1)
# 上下文向量 (context_vector) 求和之后的形状 == (批大小,隐藏层大小)
context_vector = attention_weights * values
context_vector = tf.reduce_sum(context_vector, axis=1)
return context_vector, attention_weightsDecoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40import tensorflow as tf
from BahdanauAttention import *
class Decoder(tf.keras.Model):
def __init__(self, vocab_size, embedding_dim, dec_units, batch_sz):
super(Decoder, self).__init__()
self.batch_sz = batch_sz
self.dec_units = dec_units
self.embedding = tf.keras.layers.Embedding(vocab_size, embedding_dim)
self.gru = tf.keras.layers.GRU(self.dec_units,
return_sequences=True,
return_state=True,
recurrent_initializer='glorot_uniform')
self.fc = tf.keras.layers.Dense(vocab_size)
# 用于注意力
self.attention = BahdanauAttention(self.dec_units)
def call(self, x, hidden, enc_output):
# 编码器输出 (enc_output) 的形状 == (批大小,最大长度,隐藏层大小)
context_vector, attention_weights = self.attention.call(hidden, enc_output)
# x 在通过嵌入层后的形状 == (批大小,1,嵌入维度)
x = self.embedding(x)
# x 在拼接 (concatenation) 后的形状 == (批大小,1,嵌入维度 + 隐藏层大小)
# 注意这里是“拼接”操作,可以对比前面的大图理解
x = tf.concat([tf.expand_dims(context_vector, 1), x], axis=-1)
# 将合并后的向量传送到 GRU
output, state = self.gru(x)
# 输出的形状 == (批大小 * 1,隐藏层大小)
output = tf.reshape(output, (-1, output.shape[2]))
# 输出的形状 == (批大小,vocab)
x = self.fc(output)
return x, state, attention_weights
5、模型构建和训练
1 | import os |
6、跑一下
1 | import utils.preprocessor as up |
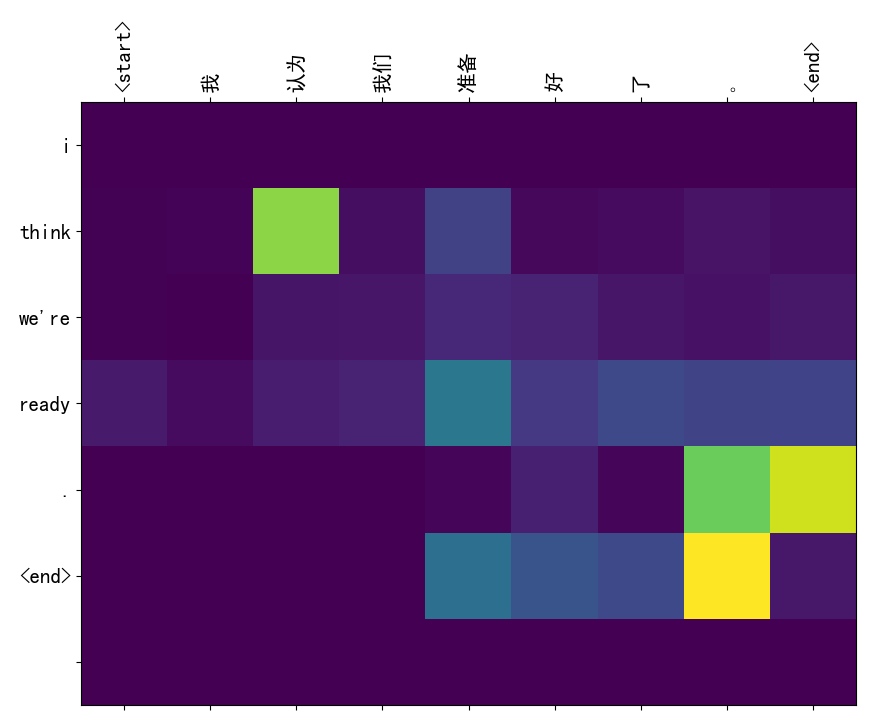
明显可以看到对于某个目标词,输入里的不同词贡献度很不一样,尤其在对角线上有明显对应关系的两个词,例如:(认为,think)、(准备,ready)等等。
6.4.3 Attention机制的基本结构
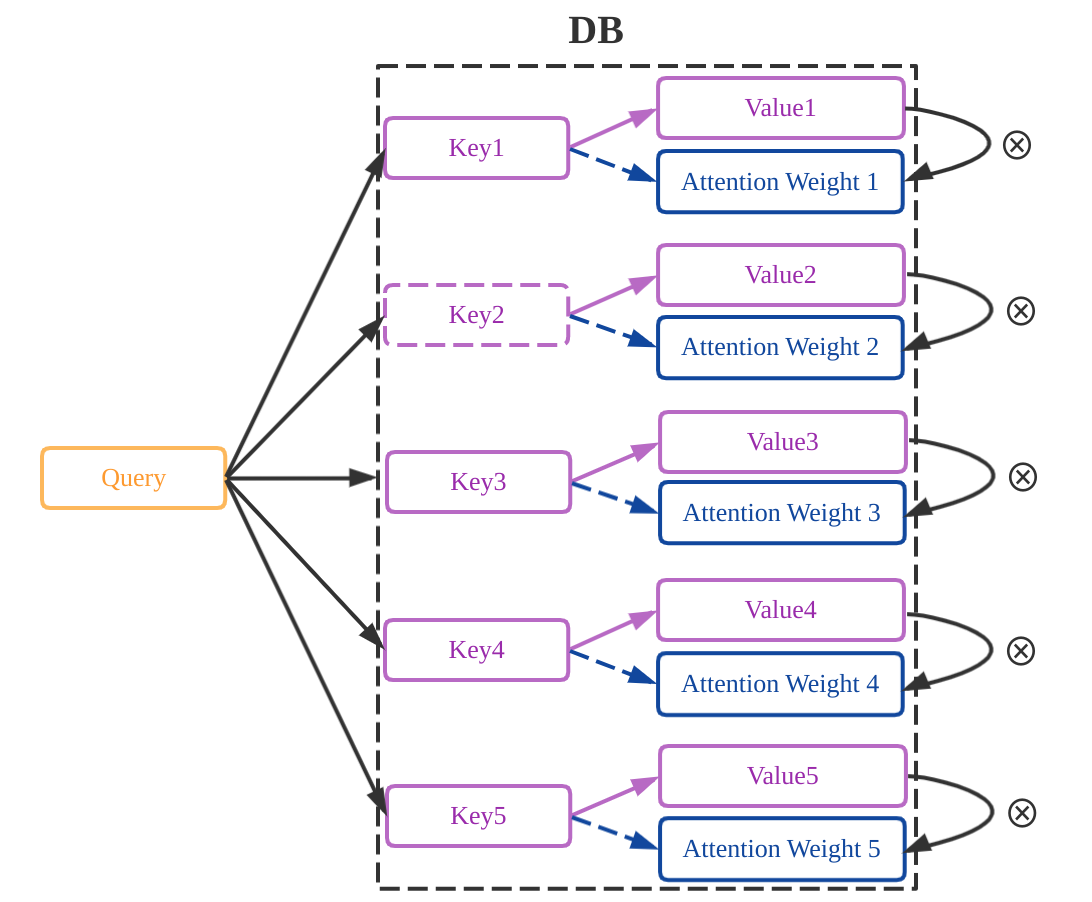
整个过程就像是用Query去数据库中扫描Key,并取出Key所对应的Value,通过计算Query与Key的相似度,来决定这些Value的最终贡献,公式表示为: \[ Attention\_Value(Q,K,V)=Normalization(Similarity(Q,K))\cdot V \] 其中,\(Similarity\)为相似度函数,\(Normalization\)为归一化函数。 例如: 当\(Similarity\)函数为做了尺度变换的点积函数\(QK^T\)(反映了两个向量的夹角和向量的范数),\(Normalization\)为\(Softmax\)函数时,上述公式变为: \[ Attention\_Value(Q,K,V)=Softmax(\frac{QK^T}{\sqrt{d_k}})\cdot V \] 其中:\(d_k\)为Query向量和Key向量的空间维度,\(\frac{1}{\sqrt{d_k}}\)为尺度缩放因子。
一、Scaled Dot-Product Attention
上面的公式在文中被叫做:Scaled Dot-Product Attention,基本结构为:
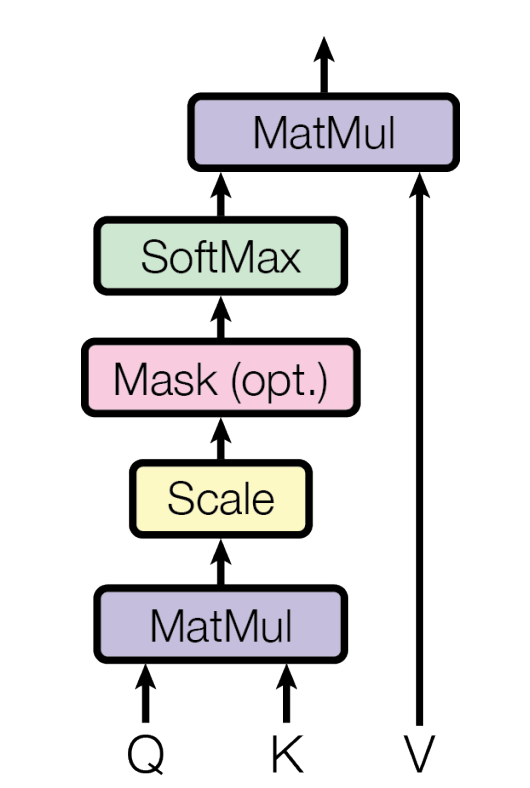
这里唯一需要强调的是Mask函数,其作用是:
1、Padding Masked
是在Encoder和Decoder都可能使用的Mask操作,因为NLP问题中很大概率会遇到每句话长度不一样,为了平衡效率与效果,我们又经常使用batch的方式训练模型,所以利用padding填充可以让每个batch中的句子长度一样,带来的问题是这些padding的内容不应该被Attention到,所以利用padding masked给padding位置一个非常大的负数值,这样通过Softmax运算后,这些位置上的概率就是0,相当于把padding位置的信息用掩码给遮蔽了。例如pytorch下:
1 | import torch |
2、Sequence Masked
是在Decoder使用的masked操作,目的是为了保证以下事实:
待预测的位置\(i\)只依赖\(i,i-1,i-2,...,0\)时刻的输出,而不能看到未来的信息(\(i+1,i+2,...,i+n\)时刻的输出),例如:
其中黄色部分为有效部分,紫色部分为masked部分,pytorch下的实现:
1 | import numpy as np |
相似度函数可以随大家定义,比如,可以是Cosine函数、欧氏距离、甚至是一个神经网络。
上面机器翻译的例子是这个公式的特殊情况,即5个隐藏状态向量即是Key又是Value,还以机器翻译为例子,如果输入和输出是一样的,就会产生所谓Self Attention的效果,可以看做是通过Attention机制捕获句子本身的内在关系。 举个例子:
许多自然环境保护主义者担心持续屠杀鲸鱼正推动这些动物走向灭绝。
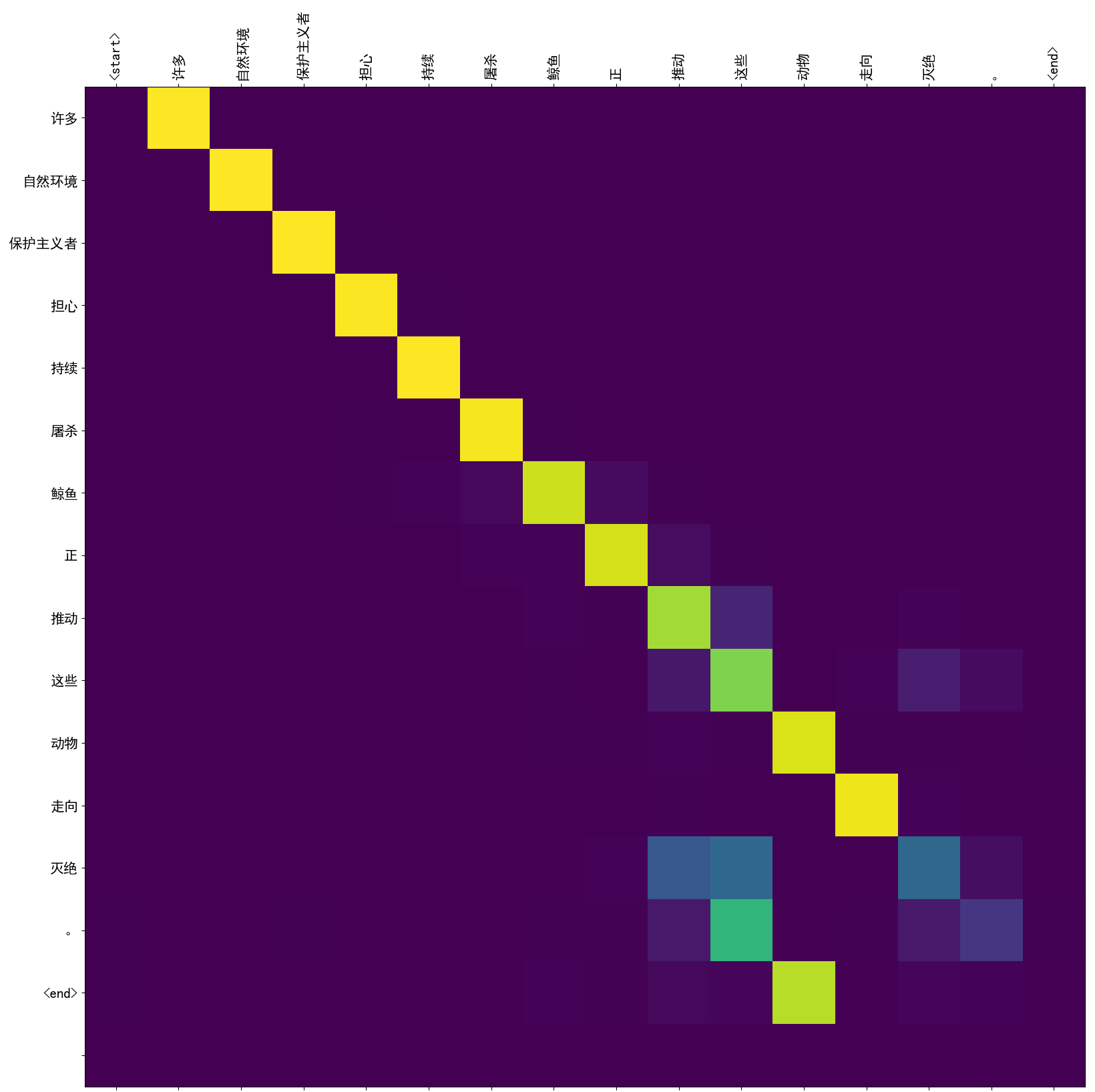
从上图可以看到“正”、“推动”、“这些”、“灭绝”对于“推动”这个词的贡献是最大的,这里既包括了距离因素也包括了语义因素,所以引入Self Attention后会更容易捕获句子中长距离依赖特征,而且更容易做并行计算。
二、Multi-Head Attention
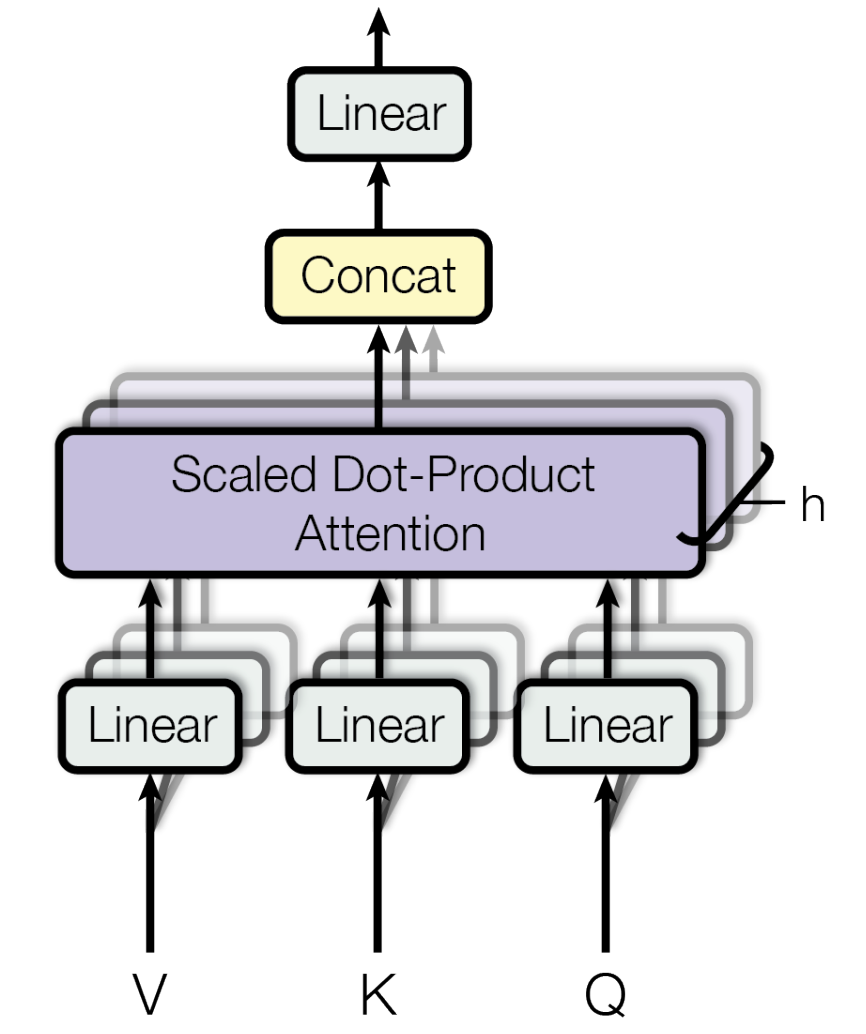
Multi-Head机制是把Q、K、V向量通过\(f(x)=x \cdot w^T+b\)做仿射映射,使得模型可以“关注”来自不同位置的、不同表示子空间的隐含信息,且由于这些向量是相互独立的,所以可以做并行计算,又因为所有“Head”维度之和等于变换前“Head”维度,所以总的计算成本没变。Multi-Head Attention由以下四部分组成:
- 仿射映射层,将向量映射拆分成若干“Multi-Head” \[f(X)=X \cdot W^T+B\]
- 对每个“Multi-Head”做Scaled Dot-Product Attention \[head_i = Scaled\_Dot\_Product\_Attention(QW_i^Q,KW_i^K,VW_i^V)\]
- 把上述输出结果做横向拼接 \[Multi\_Head\_Vector= Concat(head_1, ..., head_h)\]
- 把拼接结果做线性映射得到最终Attention输出 \[MultiHead(Q, K, V ) = Multi\_Head\_Vector \cdot W^O\]
Multi-Head的pytorch实现如下:
1 | import torch |
1 | q.shape: torch.Size([16, 60, 512]) |
三、Position-wise Feed-Forward Networks
主要用来做Attention信息的非线性组合,类似于使用了1×1卷积操作,输入序列上每个位置的词生成的Attention信息都会有一个前馈网络做这种非线性组合,注意是每个“位置”都会做但不同位置使用相同的线性变换,所以被叫做“position-wise”或“point-wise”,同时也意味着位置间可以做并行计算,公式如下: \[ FFN(x) = max(0, xW_1 + b_1)W_2 + b_2 \] 两个子层之间采用relu做激活,同样为了更好的保留输入信息和有利于梯度传播,也会增加一个残差连接,代码如下:
1 | import torch |
五、Positional Encoding & Positional Embedding
我们知道,RNN类神经网络在结构上天然具有序列学习能力,从而将词与词之间的位置关系可以很好的学到,而CNN利用zero-padding及通道编码位置信息,使得空间信息可以被捕获到,相关论文:《Global Pooling, More than Meets the Eye:Position Information is Encoded Channel-Wise in CNNs》,对没有使用这两种结构的网络就需要某种机制帮助考虑词与词在序列中的相对或绝对位置信息。这种机制应该既能隐含位置信息从而捕捉长依赖,又能做并行计算加快训练速度。通过类似word2vec这种机制能够把词的语义压缩在某个低维空间中(即Embedding的维度),且语义相近的词在空间中距离相近,同样的,除了语义距离外,词与词之间的绝对或相对距离也可以通过某种编码或Embedding的方法引入到模型中,这样既考虑了词与词之间的语义相关性又考虑了它们的距离相关性,例如:下面两个句子,分词后的“词”完全一样,语义向量也一样,但词放在不同的位置则意思南辕北辙:
我喜欢苗苗,因为她从不做作。
我从不喜欢苗苗,因为她做作。
假设,语义向量为:\(S_n\),位置向量为\(P_m\),两种做法:
1、如果\(m=n\),则\(S_n+P_n\)相当于把词的位置信息和语义信息压缩到了一个\(n\)维空间下,随后通过网络学习权重\(W\);
2、如果\(m\neq n\),则可以通过向量拼接方式实现:\([S_n;P_m]\),随后通过网络学习权重\(W_s\)和\(W_p\)。
关于\(P_m\)的生成同样也是两类方法:编码方式或者学习Embedding方式:
Positional Encoding 可以采用固定公式生成位置的绝对编码或者相对编码: 1、按照自然数递增编码,如:1、2、3...:位置间的关系本应“平等”,但顺序编码会使得数值大小严重影响这种“平等”性,产生数据bias; 2、类似one-hot或者dummy方式编码:如:10000,01000,...:编码空间和文本长度有关系,且不能编码到任意空间维度; 3、直觉上词与词局部的相对位置信息会比全局的绝对位置信息来的重要些,所以采用有界周期函数编码,能够做到一定范围内编码与文本长度无关、位置数据无bias、可以体现出词的偏序关系,例如,sine或cosine函数,一种做法是(ps:可以有无数种做法): 假设,编码维度为\(d_{model}\),则在不同维度上使用不同编码函数如下: \[ \begin{align*} PE_{(pos,2i)} &= sin(pos/10000^{2i/d_{model}})\\ PE_{(pos,2i+1)} &= cos(pos/10000^{2i/d_{model}}) \end{align*} \] 其中\(pos\)是位置,\(i\)是维度。位置编码的每个维度都对应于一个正弦曲线, 其波长形成从\(2\pi\)到\(10000 \cdot 2 \pi\)的等比级数。 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22import math
import torch
import torch.nn as nn
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_len, d_model, requires_grad=False)
position = torch.arange(0, max_len).unsqueeze(1).float()
div_term = torch.exp(torch.arange(0, d_model, 2).float() *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, input):
length = input.size(1)
return self.pe[:, :length]Positional Embedding 不使用固定函数生成位置信息隐向量,类似word embedding,通过学习方式获得,相关论文见:《Convolutional Sequence to Sequence Learning》,虽然从效果上看两者没什么区别,但个人感觉embedding方式更自然,本身被“原生集成”在了模型中,且一旦与输入序列的embedding向量做“加法”操作,计算开销可以忽略不计。
关于位置编码的一些深入研究,可以看以下文章:
1、《Rethinking Positional Encoding in Language Pre-training》
至此,Transformer里会用到的一些基本结构介绍完毕。
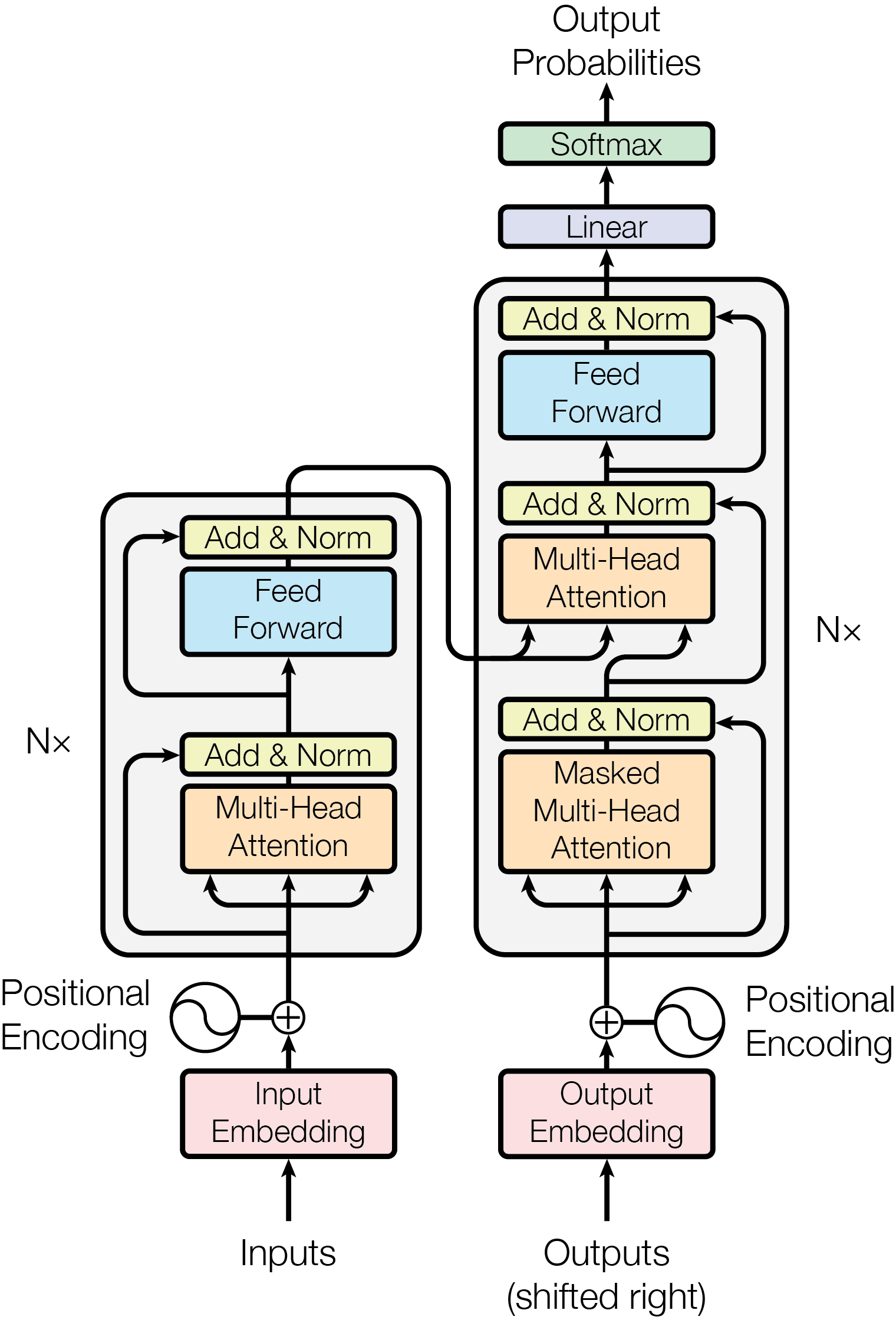
6.5. Transformer
6.5.1 基本原理
与标准Sequence2Sequence模型类似,Transformer版本的模型也是由Encoder和Decoder两大部分组成:
1、输入序列经过若干个Encoder,为序列中每个词生成一个输出。
2、Decoder利用Encoder的输出以及Attention信息预测下一个词。
大的框架如下: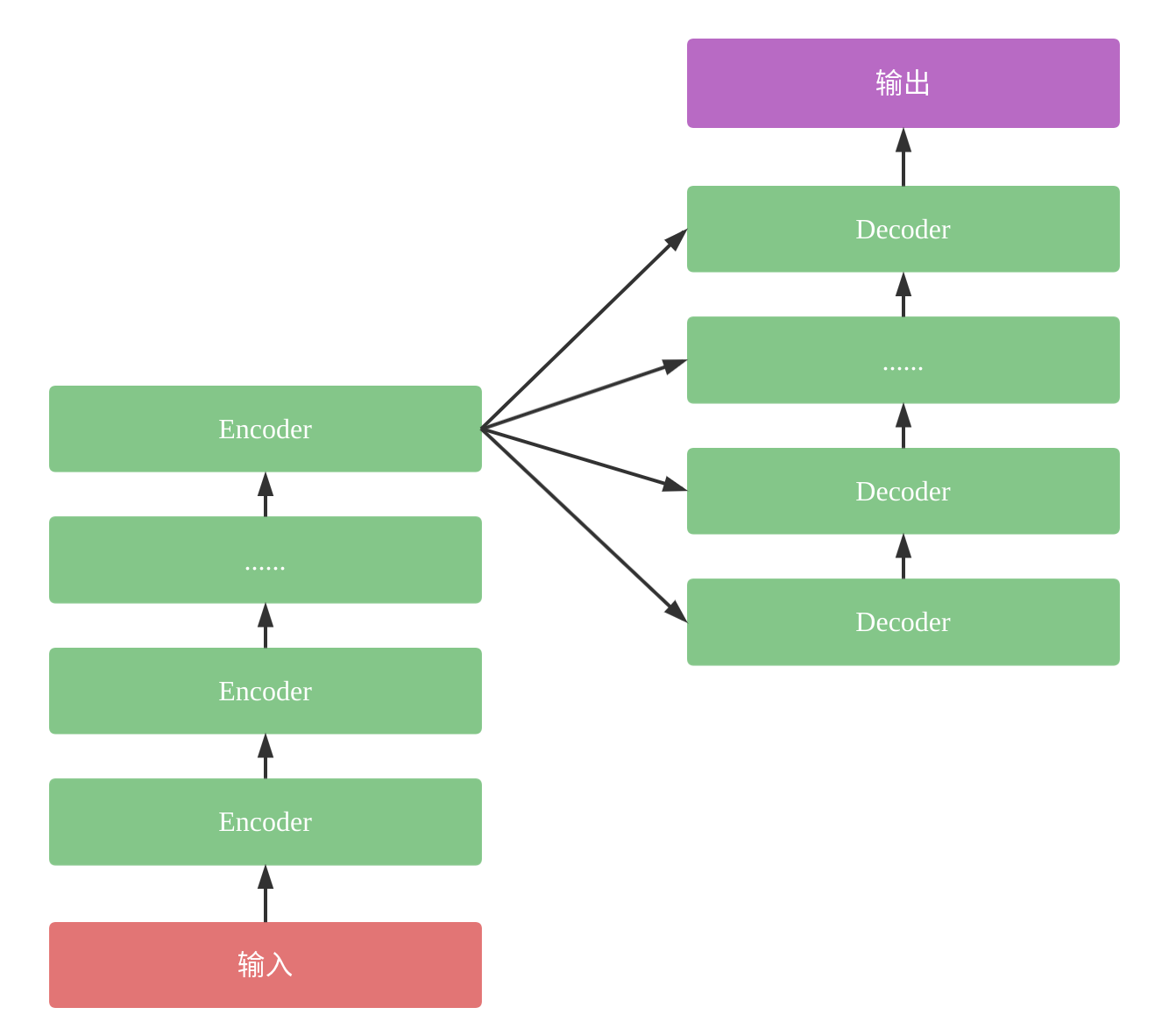
Encoder之间相互独立,每个Encoder又由两大部分组成:自身的Multi-Head Attention模块和前馈神经网络模块组成:
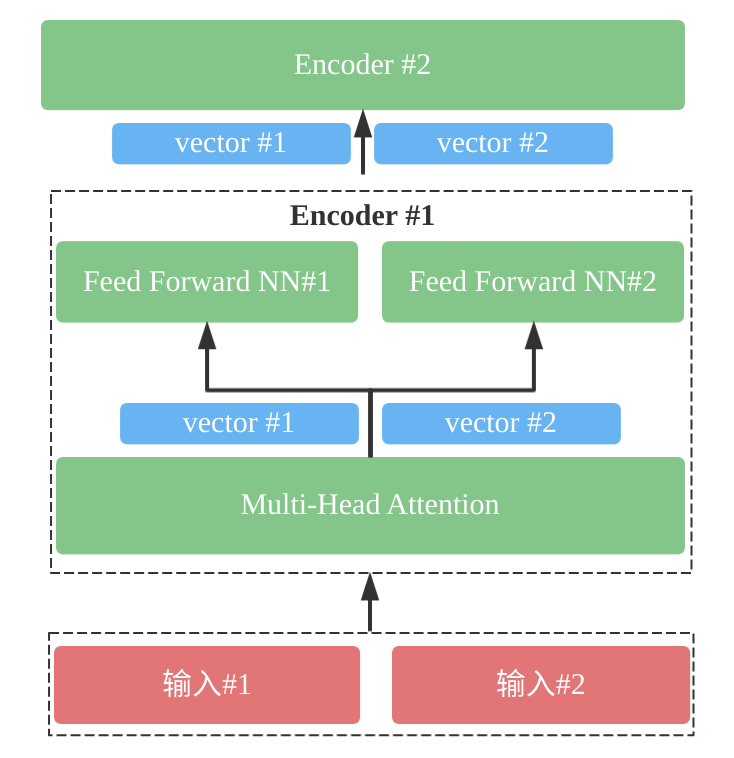
Decoder之间相互独立,每个Decoder又由三大部分组成:自身的Masked Multi-Head Attention模块、由Encoder产生并输入的Multi-Head Attention信息和前馈神经网络模块组成:
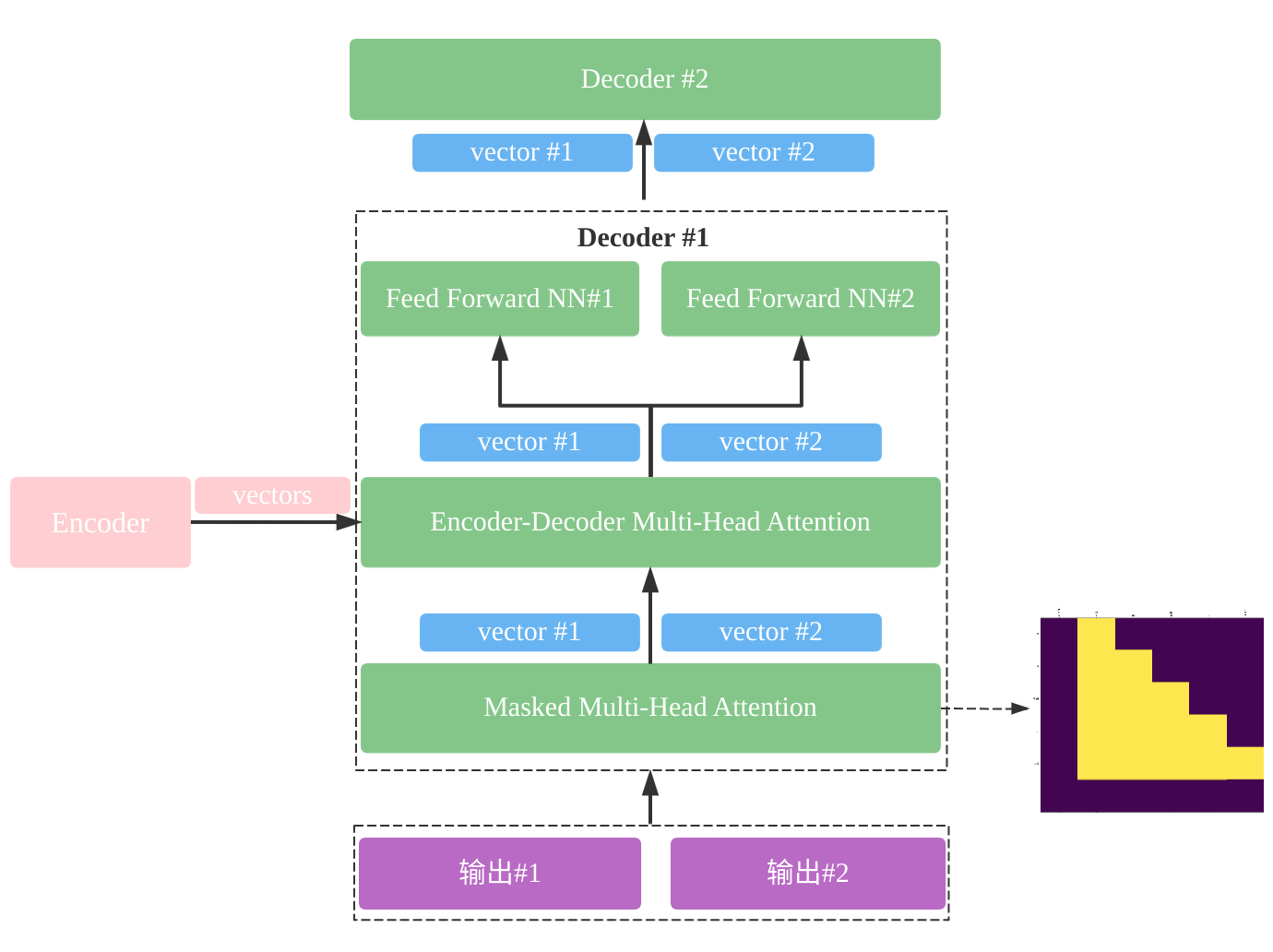
完整的标准Transformer结构如下:
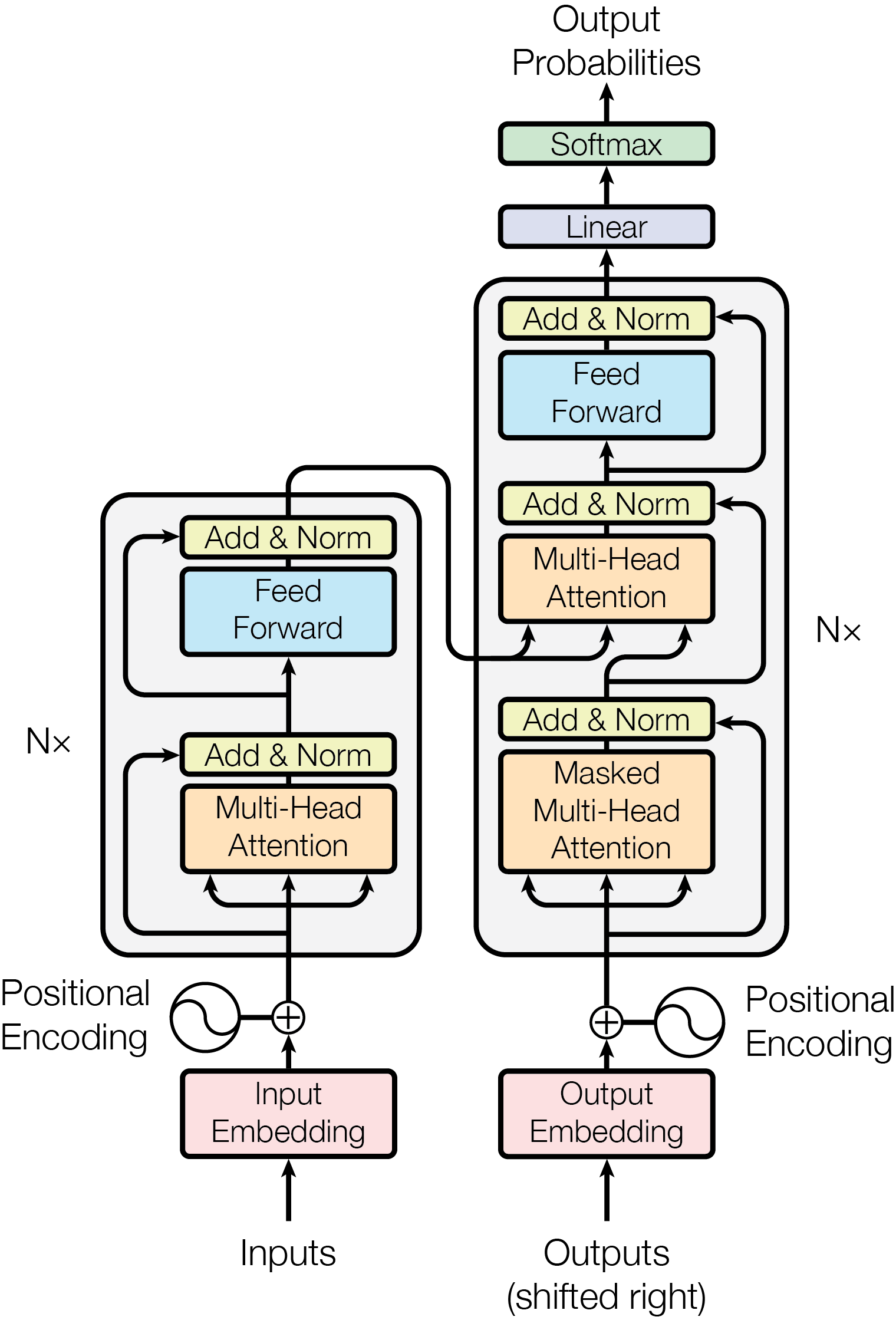
需要注意几个地方:
- Encoder的输入部分除了Word Embedding外还有描述词序的Positional Embedding,这两个向量维度相同,且执行“加法”操作后输入到Encoder;
- Encoder的Multi-Head Attention做了Padding Masked;
- Encoder每个子层都有一个残差连接(类似ResNet)帮助梯度更好更深的传播;
- Encoder的Position-wise前馈神经网络后面接了归一化层,用于降低模型方差;
- Transformer有多个Encoder串联;
- Decoder的Masked Multi-Head Attention既做了Padding Masked又做了Sequence Masked;
- Decoder的Multi-Head Attention做了Padding Masked;
- Decoder除了使用Word Embedding外还有描述词序的Positional Embedding;
- Decoder的Position-wise前馈神经网络后面接了归一化层,用于降低模型方差;
- Transformer有多个Decoder串联。
6.5.2 代码实践
Encoder Layer & Encoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80# padding填充,为公共方法
def get_attn_pad_mask(seq_q, seq_k):
batch_size, len_q = seq_q.size()
batch_size, len_k = seq_k.size()
pad_attn_mask = seq_k.data.eq(0).unsqueeze(1)
return pad_attn_mask.expand(batch_size, len_q, len_k)
class EncoderLayer(nn.Module):
"""每个Encoder层由两部分组成.
1. multi-head self-attention.
2. position-wise fully connected feed-forward network.
"""
def __init__(self, num_of_heads, dim_of_model, d_ff, dropout=0.1):
super(EncoderLayer, self).__init__()
self.mul_attn = MultiHeadAttention(num_of_heads, dim_of_model, dropout)
self.pos_ffn = PositionwiseFeedForward(dim_of_model, d_ff)
def forward(self, query, padding_mask=None):
output, attention_weights = self.mul_attn.forward(
query, query, query, mask=padding_mask)
output = self.pos_ffn(output)
return output, attention_weights
class Encoder(nn.Module):
"""Transformer有多个Encoder串联.
"""
def __init__(self, vocab_size, num_of_layers=6, num_of_heads=8, dim_of_model=512,
d_ff=512, dropout=0.1, max_length=2000):
super(Encoder, self).__init__()
# vocab_size 词典大小
# Encoder个数
self.n_layers = num_of_layers
# Multi-head数
self.num_of_heads = num_of_heads
# 模型维度
self.dim_of_model = dim_of_model
# 仿射变换输出维度
self.d_ff = d_ff
self.dropout_rate = dropout
# 序列最大长度
self.max_length = max_length
# 输入的Embedding层
self.input_emb = nn.Embedding(vocab_size, dim_of_model)
# 输入的词序embedding层
self.pos_emb = PositionalEncoding(dim_of_model, max_len=max_length)
self.dropout = nn.Dropout(dropout)
# Encoder层
self.layers = nn.ModuleList([
EncoderLayer(num_of_heads, dim_of_model, d_ff, dropout=dropout)
for _ in range(num_of_layers)])
def forward(self, padded_input):
enc_slf_attn_list = []
# 词向量Embedding
enc_outputs = self.input_emb(padded_input)
# 词向量Embedding + 词序Embedding
enc_outputs += self.pos_emb(enc_outputs)
enc_output = self.dropout(enc_outputs)
slf_attn_mask = get_attn_pad_mask(padded_input, padded_input)
# Encoder层的多级串联
for enc_layer in self.layers:
enc_output, enc_slf_attn = enc_layer(enc_output, slf_attn_mask)
enc_slf_attn_list += [enc_slf_attn]
return enc_output, enc_slf_attn_list
sample_encoder = Encoder(200)
q = torch.randint(1, 10, (64, 62))
sample_encoder_output, enc_slf_attn_list = sample_encoder(q)
print(sample_encoder_output.shape)Decoder Layer & Decoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101def get_subsequent_mask(seq):
sz_b, len_s = seq.size()
subsequent_mask = torch.triu(
torch.ones((len_s, len_s), device=seq.device, dtype=torch.uint8), diagonal=1)
subsequent_mask = subsequent_mask.unsqueeze(0).expand(sz_b, -1, -1) # b x ls x ls
return subsequent_mask
class DecoderLayer(nn.Module):
"""每个Decoder层由两部分组成.
1. multi-head self-attention.
2. encoder-decoder multi-head self-attention.
3. position-wise fully connected feed-forward network.
"""
def __init__(self, num_of_heads, dim_of_model, d_ff, dropout=0.1):
super(DecoderLayer, self).__init__()
self.mul_attn = MultiHeadAttention(num_of_heads, dim_of_model, dropout)
self.enc_attn = MultiHeadAttention(num_of_heads, dim_of_model, dropout)
self.pos_ffn = PositionwiseFeedForward(dim_of_model, d_ff)
def forward(self, dec_input, enc_output, dec_self_attn_mask=None, dec_enc_attn_mask=None):
dec_output, dec_slf_attn = self.mul_attn(
dec_input, dec_input, dec_input, mask=dec_self_attn_mask)
dec_output, dec_enc_attn = self.enc_attn(
dec_output, enc_output, enc_output, mask=dec_enc_attn_mask)
dec_output = self.pos_ffn(dec_output)
return dec_output, dec_slf_attn, dec_enc_attn
class Decoder(nn.Module):
"""Transformer有多个Decoder串联.
"""
def __init__(self, tgt_vocab_size, num_of_layers=6, num_of_heads=8, dim_of_model=512,
d_ff=512, dropout=0.1, max_length=2000):
super(Decoder, self).__init__()
# vocab_size 词典大小
# Encoder个数
self.n_layers = num_of_layers
# Multi-head数
self.num_of_heads = num_of_heads
# 模型维度
self.dim_of_model = dim_of_model
# 仿射变换输出维度
self.d_ff = d_ff
self.dropout_rate = dropout
# 序列最大长度
self.max_length = max_length
self.tgt_emb = nn.Embedding(tgt_vocab_size, dim_of_model)
self.positional_encoding = PositionalEncoding(dim_of_model, max_len=max_length)
self.dropout = nn.Dropout(dropout)
# Decoder层串行级联
self.layers = nn.ModuleList([
DecoderLayer(num_of_heads, dim_of_model, d_ff, dropout=dropout)
for _ in range(num_of_layers)])
# 映射目标词维度空间到词典表维度空间
self.tgt_word_prj = nn.Linear(dim_of_model, tgt_vocab_size, bias=False)
nn.init.xavier_normal_(self.tgt_word_prj.weight)
def forward(self, padded_input, encoder_padded_outputs, dec_enc_attn_mask=None):
# multi-head self-attention 和 encoder-decoder multi-head self-attention的attention信息
dec_slf_attn_list, dec_enc_attn_list = [], []
dec_self_attn_subsequence_mask = get_subsequent_mask(padded_input)
dec_self_attn_pad_mask = get_attn_pad_mask(padded_input,
padded_input)
dec_self_attn_mask = (dec_self_attn_pad_mask + dec_self_attn_subsequence_mask).gt(0)
dec_output = self.dropout(self.tgt_emb(padded_input) +
self.positional_encoding(padded_input))
# 多个Decoder层串行执行.
for layer in self.layers:
dec_output, dec_slf_attn, dec_enc_attn = layer(
dec_output, encoder_padded_outputs,
dec_self_attn_mask=dec_self_attn_mask,
dec_enc_attn_mask=dec_enc_attn_mask)
dec_slf_attn_list += [dec_slf_attn]
dec_enc_attn_list += [dec_enc_attn]
# 把目标词维度映射到词典维度
seq_logit = self.tgt_word_prj(dec_output)
return seq_logit, dec_slf_attn_list, dec_enc_attn_list
sample_decoder = Decoder(tgt_vocab_size=8000)
q = torch.randint(1, 10, (64, 26))
output, dec_slf_attn_list, dec_enc_attn_list = sample_decoder(padded_input=q,
encoder_padded_outputs=sample_encoder_output)
print(output.shape)Transformer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Transformer(nn.Module):
"""Transformer构建.
"""
def __init__(self, vocab_size=8000):
super(Transformer, self).__init__()
self.encoder = Encoder(vocab_size)
self.decoder = Decoder(vocab_size)
def forward(self, padded_input, padded_target):
encoder_padded_outputs, enc_slf_attn_list = self.encoder(padded_input)
pred, dec_slf_attn_list, dec_enc_attn_list = self.decoder(padded_target, encoder_padded_outputs)
return pred, enc_slf_attn_list, dec_slf_attn_list, dec_enc_attn_list
model = Transformer()
q = torch.randint(1, 10, (64, 26))
t = torch.randint(1, 10, (64, 26))
pred, *_ = model(q, t)
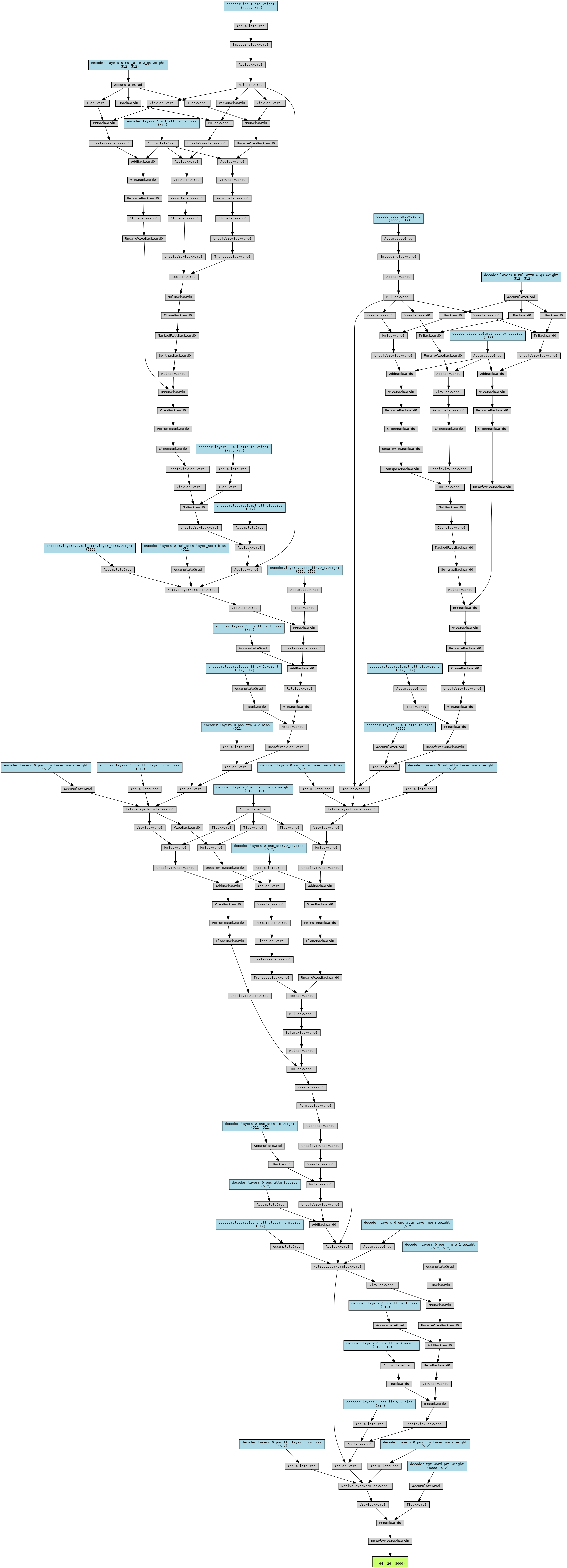
print(pred.shape)为方便可视化,设置Encoder和Decoder的num_of_layers=1,网络结构如下:
![]()
 洛伦茨系统
洛伦茨系统