业精于勤，荒于嬉；行成于思，毁于随。

花晨月夕

0%

有趣的微积分

发表于 分类于 ， 阅读次数： Valine：
本文字数： 5.8k 阅读时长 ≈ 5 分钟

本文从无穷小的角度对微积分的来由做了简单介绍，希望从另外一个视角看待微分与积分。

有趣的微积分

印象里我是上大一才开始学习微积分的，那个时候觉得学这个只是为了考试，抱着考高分拿奖学金的心态，没太意识到它的真实作用，随着工作年头的增加，对它的认识也从粗浅变得没那么粗浅了，微积分真的是一个伟大的发明，它已经改变了人类的进程并且在未来也将继续改变。 本文是对相关知识的回顾，大部分学习内容来源于《微积分的力量》这本书，温故而知新。（ps：中国先秦时代的思想依然指引着我们）

变化率与导数

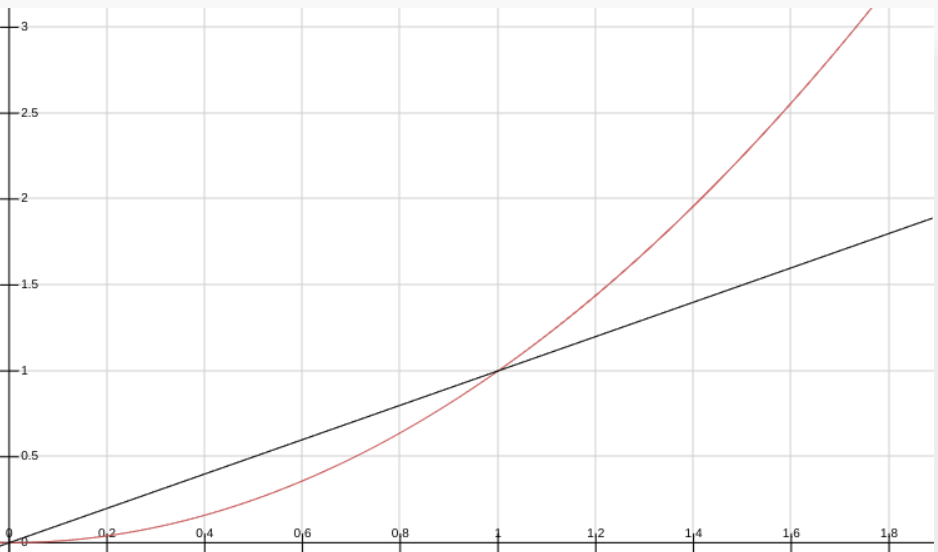
俗话说变化才是这个世界永恒不变的主题，有变化就有变化率，而世间因果或者相关关系总是由因变量和自变量组成：\(y=f(x)\)，变化率即是刻画由于自变量的变化导致因变量变化的“多块？”、“多陡？”、“多不稳定？”、“多......？”，通常表示为：\(\frac{\Delta y}{\Delta x}\)，想象我们去爬下面的两座山：

图1

显然,黑色的山，我们从山脚爬到山顶的加速度是恒定不变的，在任何一个点爬山难度都一样(忽略越往高空气越稀薄之类的因素:))，而红色的山陡峭不一，山脚的加速度和山腰的加速度完全不一样，在任何一点爬山难度不一样且越往高处爬越难。其实现实中的问题变化率几乎不太可能是恒定的，所以如何定义不断改变的变化率是微积分要解决的大难题之一。

最直观的理解是：变化率不再是一个恒定值，它是一个函数。怎么定义这个函数呢？我们的祖先给了答案，当一个大的问题太复杂无法一下子解决，古人教我们先把它变成一系列小问题，所有小问题解决则大问题也随之解决。这就是微分学要做的事：依据无穷小法则把这些小问题拆解为无穷小的小问题，分析和解决这些小问题后，利用积分学把它们重新组合起来，而定义变化率函数的这个问题就是通过定义导数来拆解解决的，即：\(\frac{dy}{dx}\)，里面的\(dx\)、\(dy\)就是这些无穷小的问题，所以从另一个角度看，微积分就是描述“变化”的数学。

微积分有三大核心问题：

  • 问题1：已知曲线的函数形式，求曲线任意一点的斜率
  • 问题2：已知曲线的斜率函数，求曲线函数形式
  • 问题3：已知曲线的函数形式及其上任意一点，求曲线在该点下方的面积
图2

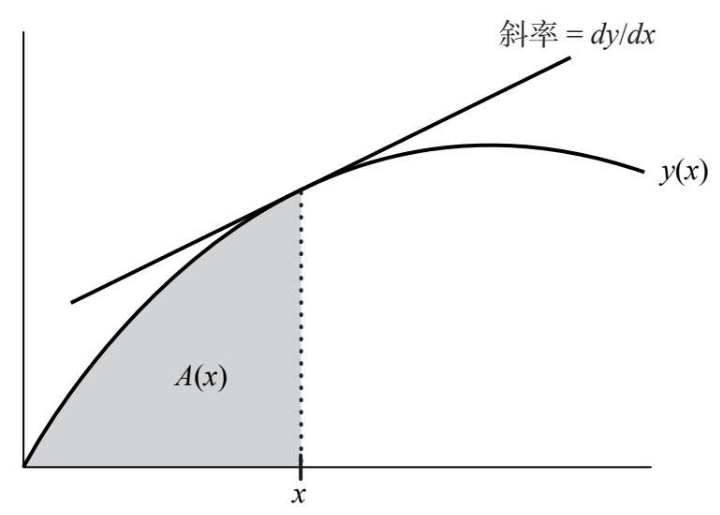
看这个图，可以得出3个基本结论：

1、斜率衡量的是这条曲线的变化率

2、问题1与问题2是对偶问题（Duality）

3、面积衡量的是变化率的累积(Cumulative)

线性函数变化率

自变量和因变量呈现线性关系可以近似生活中的很多场景，比如，汽车的均速直线运动，再比如上面的理想爬山运动：

图3

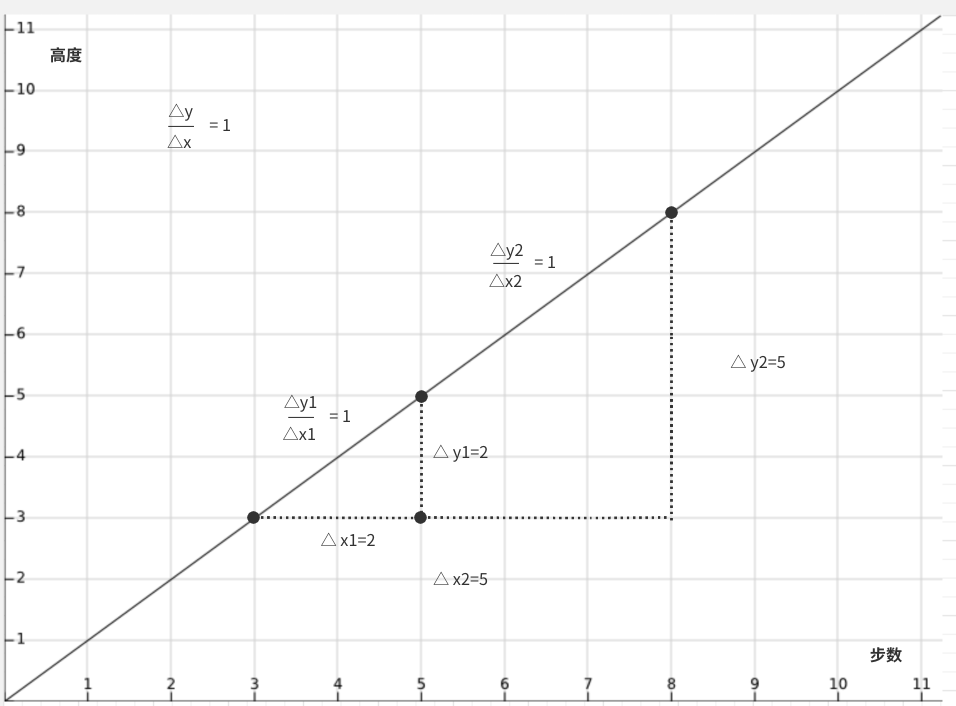
不管是大人迈一次步子，还是3岁小孩儿迈一次步子，高度的变化率总是一定的。 在机器学习中有一类叫广义线性模型（GLM）的方法就是把现实问题做了一系列假设，让它变成一个线性问题，这样问题建模和求解起来就简单了很多。

非线性函数变化率

自变量和因变量呈现非线性关系其实才是现实世界的主流，比如，钟摆运动画出的弧线、爬山运动等等。这些函数的特点是其上任何一点的变化率都不一样，以\(y=x^2\)为例：

图4

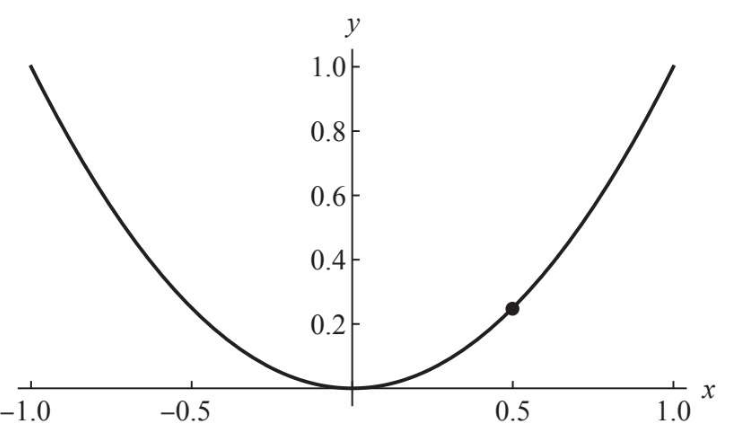
我们要解决的问题是：如何得到这个抛物线上任何一点的切线斜率？ 从最简单情况来看，原点(0,0)的切线显然是横轴，它是水平的，所以切线斜率为0，其他点就没那么明显了，我们模仿2000年前阿基米德求圆周率的做法，用无穷原则把曲线切分成无穷多个小线段，以图中(0.5,0.25)为例，取上图\(x<0.7\)那部分的图像：

图5

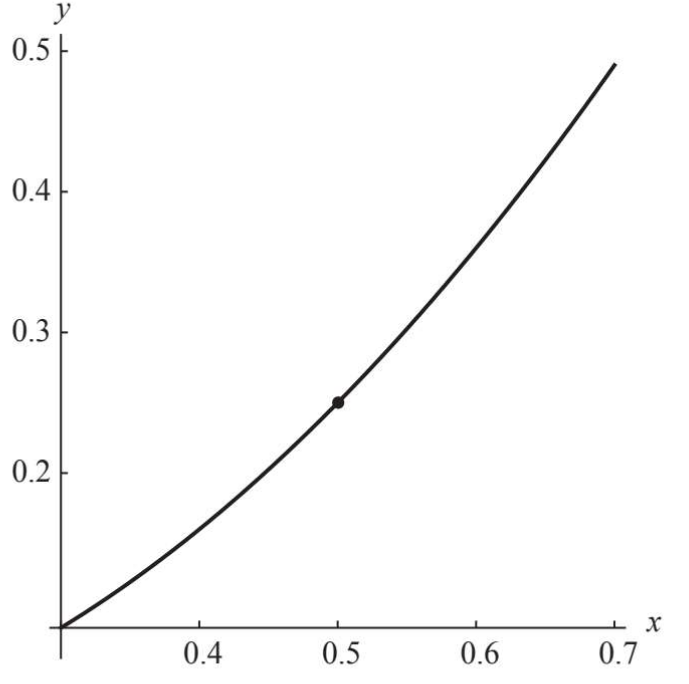
可以看到曲线没那么弯曲了，更进一步，我们取\(0.49<x<0.51\)这部分图像：

图6

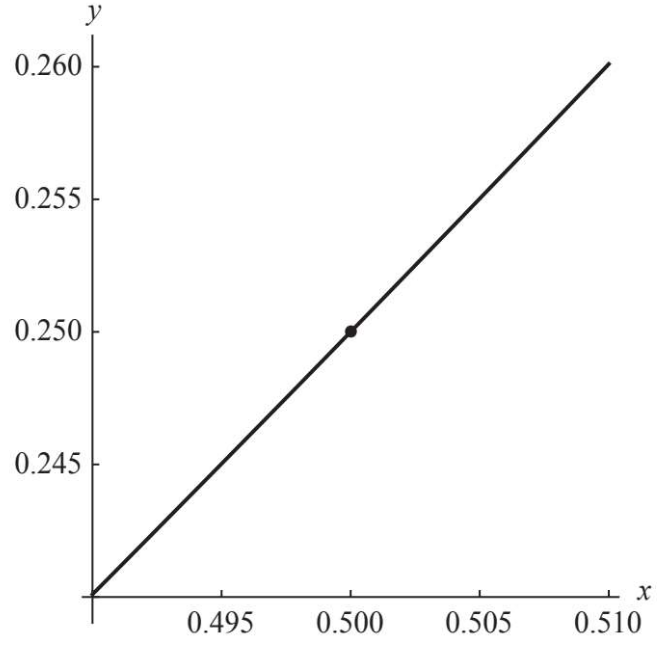
曲线看上去几乎成为直线了，这个时候切线的斜率是：\(\frac{dy}{dx}=\lim\limits_{\Delta x \to 0}{\frac{\Delta y}{\Delta x}}\)，写个小程序模拟这个无穷小和自变量的关系：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#!/usr/bin/python
# Write Python 3 code in this online editor and run it.
i=0
x1=0.5
y1=0.25
while(True):
	i=i+1
	x2=0.51-0.0001*i
	y2=x2*x2
	deltax=x2-x1
	deltay=y2-y1
	if x2<=0.5:
		break
	print(deltay/deltax,'|',2*x1)
得到关系：

\(\frac{dy}{dx}\)\(2x\)
1.00989999999999821.0
1.0098000000000021.0
1.00969999999999921.0
1.00960000000000071.0
1.00950000000000141.0
1.0094000000000011.0
1.00929999999999941.0
1.00920000000000281.0
1.00909999999999881.0
1.00899999999999971.0
1.00889999999999951.0
1.00879999999999811.0
1.0087000000000021.0
1.00859999999999821.0
1.00849999999999951.0
1.00839999999999971.0
1.00829999999999861.0
1.00820000000000291.0
1.00809999999999931.0
1.00800000000000111.0
1.00790000000000161.0
1.00780000000000071.0
1.00769999999999871.0
1.00760000000000231.0
1.00749999999999721.0
1.00739999999999831.0
1.00729999999999791.0
1.00720000000000341.0
1.00711.0
1.0070000000000031.0
1.00689999999999661.0
1.00679999999999641.0
1.00670000000000281.0
1.00659999999999971.0
1.00650000000000331.0
1.00639999999999661.0
1.0062999999999971.0
1.00619999999999551.0
1.00610000000000151.0
1.00599999999999671.0
1.00589999999999941.0
1.00580000000000021.0
1.00569999999999941.0
1.00559999999999651.0
1.00550000000000161.0
1.0053999999999951.0
1.00529999999999631.0
1.00519999999999591.0
1.0051000000000041.0
1.00499999999999941.0
1.0049000000000041.0
1.00479999999999461.0
1.00469999999999461.0
1.00460000000000441.0
1.00449999999999971.0
1.00440000000000551.0
1.0042999999999961.0
1.00419999999999671.0
1.00409999999999471.0
1.0040000000000041.0
1.0038999999999971.0
1.00380000000000111.0
1.0037000000000031.0
1.00360000000000161.0
1.00349999999999741.0
1.00340000000000631.0
1.00329999999999561.0
1.00319999999999831.0
1.00309999999999791.0
1.00299999999999371.0
1.00290000000000481.0
1.00279999999999331.0
1.00269999999999751.0
1.0025999999999981.0
1.00249999999999421.0
1.00240000000000881.0
1.00229999999999621.0
1.00220000000000261.0
1.00210000000000491.0
1.0020000000000021.0
1.00189999999999341.0
1.00180000000000851.0
1.00169999999998671.0
1.00159999999999051.0
1.00149999999998761.0
1.00140000000001651.0
1.0012999999999991.0
1.0012000000000161.0
1.00109999999997611.0
1.00099999999997321.0
1.00090000000001971.0
1.00079999999999521.0
1.00070000000002811.0
1.00059999999996171.0
1.00049999999995891.0
1.0004000000000671.0
1.0003000000000271.0
1.00019999999989471.0
1.00009999999994741.0

随着\(\Delta x\)越来越小，\(\frac{dy}{dx}\)的取值越来越接近\(2x\)，可以猜测函数\(y=x^2\)上的任意一点切斜斜率为\(2x\),即\(\frac{dy}{dx}=2x\)，由于上学时老师直接讲的是导数的结论，我们是站在牛顿、莱布尼茨巨人们的肩上的，所以大家想当然就觉得这不是很简单的么，我们都知道答案，大家试着把认知退回到知道答案前，思考下怎么证明以上观察到的结果是普适的，怎么抽象出一般范式？

微积分隐秘的力量

无穷小量

无穷小量是一种概念里存在的东西，它大于0但又无限接近0的数。并且无穷小量的大小是不同的。一个无穷小量的无穷小部分还要更加小得多，我们称之为二阶无穷小量，类似的还有三阶无穷小，......，\(n\)阶无穷下。

还是上面的例子：\(0.5^2=0.25\)，那么\(0.50001^2\)呢？

我们知道它肯定大于\(0.25\)，但到底大多少呢？

答案是：\(0.50001^2=0.25001000009999996\)，而小数点两位后(\(0.25\)后)的这个小数又是由两个部分组成的，即：

\(0.00001000009999996=0.00001+0.00000000009999996\)，显然前半部分“很小”，后半部分则“超级小”。

假设：上面例子中\(x\)发生了正向的微小扰动\(\Delta x\)，变成了\(x+\Delta x\)，则有：

\[(x+\Delta x)^2=x^2+2x\Delta x+{\Delta x}^2\] 把\(x=0.5\)代进去，则有： \[(0.5+\Delta x)^2=0.25+\Delta x+{\Delta x}^2\] \(\Delta x\)和\({\Delta x}^2\)分别对应“很小”的那部分一阶无穷小和“超级小”的那部分二阶无穷小。

微分

古人教导我们，关注问题的主要矛盾和矛盾的主要方面，对于上面的无穷小量，可以关注“很小”这个矛盾的主要方面，忽略“超级小”这个次要方面，这个是微积分背后的核心观点，这种忽略思维会给我们带来巨大好处，还是上面的例子： \[(0.5+\Delta x)^2=0.25+\Delta x+{\Delta x}^2\] 抛弃掉“超级小”部分，并做下符号变换，得到： \[(0.5+d x)^2=0.25+d x\] 那么要计算\(y=x^2\)这个曲线上任意一点\(x\)的切线斜率\(\frac{dy}{dx}\)，还需要计算\(dy\)出来，方法如下： \[y+dy=(x+dx)^2\] 推导下得到： \[y+dy=x^2+2xd x+{d x}^2\] 忽略掉“超级小”的二阶无穷小，得到： \[y+dy=x^2+2xd x\] 因为：\(y=x^2\)，所以得到： \[dy=2xdx\] 于是斜率公式为： \[\frac{dy}{dx}=2x\] 当\(x=0.5\)时，该点切斜斜率为：\(2 \times0.5=1\)，和上面结果一致，至此也就推导出了这个范式。

面积与斜率的关系

微积分基本定理认为，当横坐标\(x\)取值向右滑动时，曲线下方的面积会以\(f(x)\)的速率逐渐增大。因此，\(f(x)\)是\(A(x)\)的导数，总结下就是： \[A(x)\Rightarrow^{导数}y(x)\Rightarrow^{导数}\frac{dy}{dx}\] 其中：\(A(x)\)为曲线下方面积，\(y(x)\)为曲线本身，\(\frac{dy}{dx}\)为曲线斜率。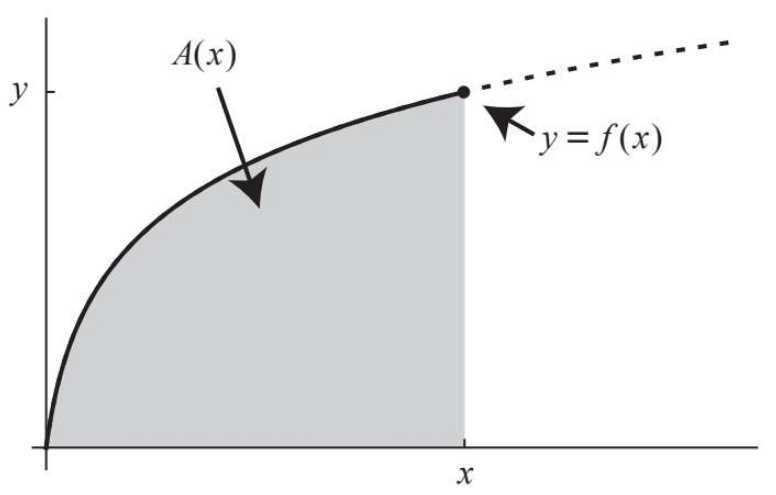
图7
给\(x\)增加一个无穷小量\(dx\)，面积\(A(x)\)会变化多少？逻辑上应该是\(dA\)，新的面积是：\(A+dA\)，直观展示为：
图8
显然\(dA\)等于\(x\)和\(x+dx\)之间这个灰色的无限细长竖条的面积。这个竖条是一个高为\(y\)、底为\(dx\)的矩形，它的面积等于\(ydx\)，即\(f(x)dx\)，而这里我们忽略的那个“超级小”的无穷量就是这个矩形上面的小帽子：
图9

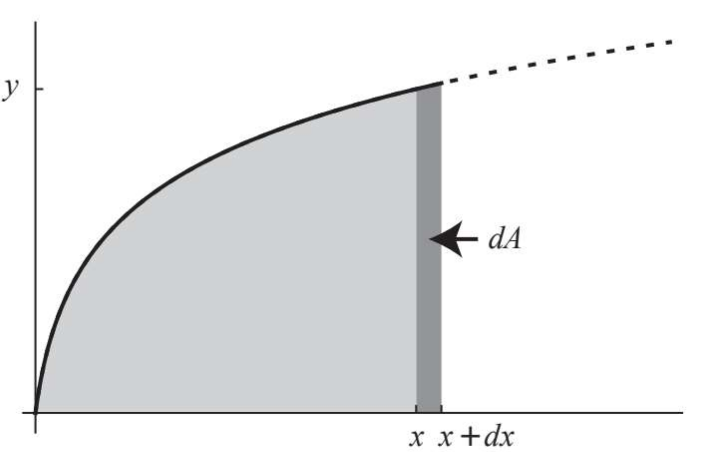
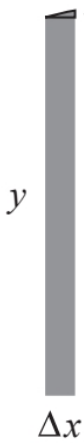
整理一下就得到： \[\frac{dA(x)}{dx}=f(x)\] 当曲线下方的面积由无穷多个无穷小的矩形竖条面积组成时，就可以得到经典形式： \[A(x)=\int_0^xf(x)dx\]

积分符号\(\int\)是莱布尼茨1677年引入并在1686年正式发表的，当时他把“微积分”叫做“a calculus”和“my calculus”（有点我的小甜甜的味道）。

至此，总结下，从无穷量角度去看待微积分，会发现它最初的“原味”，我们解决实际问题时因为有太多的“历史经验”，让我们觉得很多东西想当然，需要意识到并练习抛开这些想当然的“法”去理解“道”。

相关文章推荐

欢迎关注我的其它发布渠道